圆方树学习笔记
圆方树是优秀的图论算法,从仙人掌图向无向图扩展,利用割点和点双联通分量的性质,实现了图向树的转换。
对仙人掌的处理:圆方树——处理仙人掌的利器
而且实现十分简单
算法思路
前置知识
割点和桥,点双联通分量。
思路
对于一个无向图,圆方树理解可以如下:
- 原图中点是圆点。
- 图中的每一个点双联通分量新建一个点,这些点称为方点。
- 删除原图中的边,每一个圆点向包含其的点双对应的方点连边。
注意:如果两点不是属于同一点双,而又有边相连,那么我们把这两点看做是一个点双。
下图是一个图示:
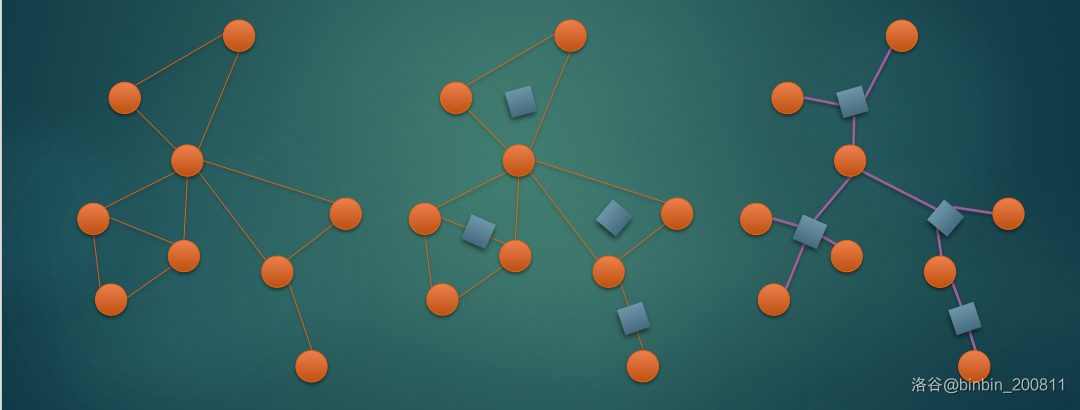
可以使用 tarjin 算法快速建出圆方树:
//G 是原图边,Tr 是圆方树边
void tarjin(int u)
{
dfn[u]=low[u]=++cok;
st[++tp]=u;
for(int i=G.head[u];i;i=G.edge[i].nxt)
{
int v=G.edge[i].to;
if(!dfn[v])
{
tarjin(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u])//出现点双,建方点连边
{
Tr.add(++tx,u);
Tr.add(u,tx);
int x=0;
do
{
x=st[tp--];
Tr.add(tx,x);
Tr.add(x,tx);
}while(x!=v);
}
}
else low[u]=min(low[u],dfn[v]);
}
}
性质
1.圆方树上圆点只会和方点连边。
2.节点级别为 \(O(n)\)。
3.如果原图连通,那么其圆方树为一棵树。
性质1:正确性显然,方点仅会和圆点相连。
性质2:显然,原图中点双至多有 \(n\) 个,新建方点个数为 \(O(n)\) 级。关于点双至多 \(O(n)\) 个,不难发现,每次新建方点连边至少出栈一次,而每个点至多入栈一次,得证。
性质3:考虑反证法,设一直圆方树中存在环,那么环上的一个圆点至少连接两个方点,那么这个圆点至少属于两个点双。
引理:不是割点的点至多存与一个点双。阅读代码可知,不是割点的点,在构建圆方树时,与对应方点的连边出现在循环弹栈中,又至多出现一次,得证。
根据引理,环中的圆点都是割点,删除割点后图会不连通,与环的定义冲突。反证性质3成立。
实际运用
不难发现圆方树上两点之间的圆点就是任意一条简单路径都必须经过的点(割点)。
例题
例一 P4320 道路相遇
建圆方树查询两点之间圆点个数。
利用 LCA 和一下分析一下圆方树的其他性质还是挺好做的。
#include<bits/stdc++.h>
using namespace std;
const int maxm=1e6+5,maxn=5e5+5;
struct node
{
int to,nxt;
}tredge[maxm*2],edge[maxm*2];
int n,m,trtot,tot,cok,tp,tx,q;
int dfn[maxn],low[maxn],trhead[maxm],head[maxn],deep[maxm],st[maxn],fa[maxm][25];
void add(int *head,node *edge,int &tot,int x,int y)
{
tot++;
edge[tot].to=y;
edge[tot].nxt=head[x];
head[x]=tot;
}
void tarjan(int u)
{
dfn[u]=low[u]=++cok;
st[++tp]=u;
for(int i=head[u];i;i=edge[i].nxt)
{
int v=edge[i].to;
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u])
{
add(trhead,tredge,trtot,++tx,u);
add(trhead,tredge,trtot,u,tx);
int x=0;
do{
x=st[tp--];
add(trhead,tredge,trtot,tx,x);
add(trhead,tredge,trtot,x,tx);
}while(x!=v);
}
}
else low[u]=min(low[u],dfn[v]);
}
}
void dfs(int u)
{
for(int i=trhead[u];i;i=tredge[i].nxt)
{
int v=tredge[i].to;
if(!deep[v])
{
deep[v]=deep[u]+1;
fa[v][0]=u;
for(int j=1;j<=20;j++)
fa[v][j]=fa[fa[v][j-1]][j-1];
dfs(v);
}
}
}
int lca(int x,int y)
{
if(deep[x]<deep[y]) swap(x,y);
for(int i=20;i>=0;i--)
{
if(deep[fa[x][i]]>=deep[y]) x=fa[x][i];
}
if(x==y) return x;
for(int i=20;i>=0;i--)
{
if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
}
return fa[x][0];
}
int main()
{
scanf("%d%d",&n,&m);
tx=n;
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
add(head,edge,tot,x,y);
add(head,edge,tot,y,x);
}
tarjan(1);
deep[1]=1;
dfs(1);
scanf("%d",&q);
while(q--)
{
int u,v,t;
scanf("%d%d",&u,&v);
t=lca(u,v);
printf("%d\n",(deep[u]+deep[v]-deep[t]*2)/2+1);
}
}
例二 P4606 SDOI2018 战略游戏
圆方树上圆方果,圆方树下你和我。
圆方树后建虚树,欢乐多又多。
建出圆方树,然后建虚树。
维护虚树上父子点之间的圆点个数相加。
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
struct Edge
{
int tot;
int head[maxn];
struct edgenode{int to,nxt;}edge[maxn*2];
void add(int x,int y)
{
tot++;
edge[tot].to=y;
edge[tot].nxt=head[x];
head[x]=tot;
}
void clr()
{
memset(head,0,sizeof(head));
memset(edge,0,sizeof(edge));
tot=0;
}
}Tr,G;
int n,m,cok,tp,tx;
int dfn[maxn],low[maxn],deep[maxn],f[maxn][25],st[maxn],len[maxn],wz[maxn],ed[maxn];
void tarjin(int u)
{
dfn[u]=low[u]=++cok;
st[++tp]=u;
for(int i=G.head[u];i;i=G.edge[i].nxt)
{
int v=G.edge[i].to;
if(!dfn[v])
{
tarjin(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u])
{
Tr.add(++tx,u);
Tr.add(u,tx);
int x=0;
do
{
x=st[tp--];
Tr.add(tx,x);
Tr.add(x,tx);
}while(x!=v);
}
}
else low[u]=min(low[u],dfn[v]);
}
}
void dfs(int u)
{
len[u]+=(u<=n);
wz[u]=++cok;
for(int i=Tr.head[u];i;i=Tr.edge[i].nxt)
{
int v=Tr.edge[i].to;
if(!deep[v])
{
deep[v]=deep[u]+1;
f[v][0]=u;
len[v]=len[u];
for(int j=1;j<=20;j++) f[v][j]=f[f[v][j-1]][j-1];
dfs(v);
}
}
ed[u]=cok;
}
int Lca(int u,int v)
{
if(deep[u]<deep[v]) swap(u,v);
for(int i=20;i>=0;i--) if(deep[f[u][i]]>=deep[v]) u=f[u][i];
if(u==v) return u;
for(int i=20;i>=0;i--) if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
return f[u][0];
}
int a[maxn];
bool vis[maxn];
bool cmp(int x,int y){return wz[x]<wz[y];}
bool isfa(int u,int v){return st[u]<st[v]&&ed[u]>=ed[v];}
int main()
{
int _;
scanf("%d",&_);
while(_--)
{
memset(deep,0,sizeof(deep));
Tr.clr();
G.clr();
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
memset(f,0,sizeof(f));
memset(st,0,sizeof(st));
memset(len,0,sizeof(len));
memset(wz,0,sizeof(wz));
memset(ed,0,sizeof(ed));
cok=tp=tx=0;
scanf("%d%d",&n,&m);
tx=n;
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
G.add(u,v);
G.add(v,u);
}
tarjin(1);
deep[1]=1;
len[1]=1;
cok=0;
dfs(1);
int p;
scanf("%d",&p);
while(p--)
{
int s;
scanf("%d",&s);
for(int i=1;i<=s;i++) scanf("%d",&a[i]),vis[a[i]]=1;
sort(a+1,a+s+1,cmp);
int sl=s;
for(int i=1;i<s;i++)
{
int lca=Lca(a[i],a[i+1]);
if(!vis[lca])
{
vis[lca]=1;
a[++sl]=lca;
}
}
sort(a+1,a+sl+1,cmp);
int ans=-2*s;
for(int i=1;i<=sl;i++)
{
int u=a[i],v=a[i%sl+1];
ans+=len[u]+len[v]-2*len[Lca(u,v)];
}
if(Lca(a[1],a[sl])<=n) ans+=2;
printf("%d\n",ans/2);
for(int i=1;i<=sl;i++) vis[a[i]]=0;
}
}
}