【模板】树状数组 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上
x -
求出某区间每一个数的和
输入格式
第一行包含两个正整数 n,m ,分别表示该数列数字的个数和操作的总个数。
第二行包含 n 个用空格分隔的整数,其中第 i 个数字表示数列第 i 项的初始值。
接下来 m 行每行包含 3 个整数,表示一个操作,具体如下:
-
1 x k含义:将第x个数加上k -
2 x y含义:输出区间[x,y]内每个数的和
输出格式
输出包含若干行整数,即为所有操作 2 的结果。
样例 #1
样例输入 #1
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
样例输出 #1
14
16
提示
【数据范围】
对于 30% 的数据,1 ≤ n ≤ 8,$1 ≤ m ≤ 10;
对于 70% 的数据,1 ≤ n,m ≤ 10^4;
对于 100% 的数据,1 ≤ n,m ≤ 5 * 10^5。
数据保证对于任意时刻,a 的任意子区间(包括长度为 1 和 n 的子区间)和均在 [-2^{31}, 2^{31}) 范围内。
样例说明:
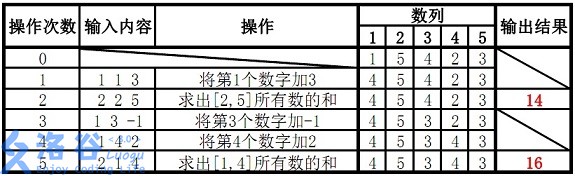
故输出结果14、16
思路:树状数组?线段树?
三步走!!!
-
建树
void buildtree(int k,int l,int r){ if(l==r){//l==r时就是分到只剩一个了 f[k]=a[l];//此时返回叶子结点数据(也就是原数据) return; } //以下三步,就是找左右儿子 //这个过程与归并排序的递归过程类似可以去看一下 //其中2k和2k+1代表的是当前结点的左右子结点(这一步不详细展开,可以自己画图尝试) int mid=(l+r)>>1; buildtree(2*k,l,mid); buildtree(2*k+1,mid+1,r); //父亲结点=儿子结点的和 f[k]=f[2*k]+f[2*k+1]; } -
修改数据
void add(int k,int l,int r,int x,int y){//k表示第几个结点,l、r表示区间,x表示第几个值要修改,y表示要使原值+y //因为每次找到的都是第x个元素的父亲结点的父亲的父亲……所以直接+y f[k]+=y;//包含结点x的值都需要+y if(l==r) return;当递归到l=r即为只有一个元素返回 int mid=(l+r)>>1; if(x<=mid) add(2*k,l,mid,x,y);如果是在左子树就往左找 else add(2*k+1,mid+1,r,x,y);如果是在右子树就往右边找 } -
计算答案
int calc(int k,int l,int r,int s,int t){//s、t表示要求的区间反围 if(l==s && r==t)//如果区间缩小到包含原数据区间的子区间反围即返回 return f[k]; int mid=(l+r)>>1; if(t<=mid) return calc(2*k,l,mid,s,t);//如果当前要求的区间范围在左子树就往左边找 else//在右子树或者部分在右子树 if(s>mid) return calc(2*k+1,mid+1,r,s,t);//在右子树上 else return calc(2*k,l,mid,s,mid)+calc(2*k+1,mid+1,r,mid+1,t);//部分在右子树 }
tips:这个树状数组应该开多大?
开4n。参考证明连接:线段树需要开4倍区间大小的数组的原因_线段树数组一般开 n*4 的大小-CSDN博客
(本文章仅供学习交流如有侵权请私信立刻删除)
AC Code
// Problem:
// P3374 【模板】树状数组 1
//
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3374
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<iostream>
#include<algorithm>
//#include<cstdio>
#define ll long long
#define endl '\n'
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>(b);i--)
#define N 2000100 //1e6+100
#define M 500010
using namespace std;
int f[N],a[M],n,m;
void buildtree(int k,int l,int r){
if(l==r){
f[k]=a[l];
return;
}
int mid=(l+r)>>1;
buildtree(2*k,l,mid);
buildtree(2*k+1,mid+1,r);
f[k]=f[2*k]+f[2*k+1];
}
void add(int k,int l,int r,int x,int y){
f[k]+=y;
if(l==r) return;
int mid=(l+r)>>1;
if(x<=mid) add(2*k,l,mid,x,y);
else add(2*k+1,mid+1,r,x,y);
}
int calc(int k,int l,int r,int s,int t){
if(l==s && r==t)
return f[k];
int mid=(l+r)>>1;
if(t<=mid)
return calc(2*k,l,mid,s,t);
else
if(s>mid)
return calc(2*k+1,mid+1,r,s,t);
else
return calc(2*k,l,mid,s,mid)+calc(2*k+1,mid+1,r,mid+1,t);
}
int main(){
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>m;
rep(i,1,n)
cin>>a[i];
buildtree(1,1,n);
int t,x,y;
while(m--){
cin>>t>>x>>y;
if(t==1)
add(1,1,n,x,y);
else cout<<calc(1,1,n,x,y)<<endl;;
}
return 0;
}