#1 模板
基础最大流(最小割)
const int MAXN=5e5+5,MAXM=6e5+5;
struct E{int nxt,to,w;}e[MAXM];
int head[MAXN],cur[MAXN];
int cnt=1;
void add(int u,int v,int w){
e[++cnt]={head[u],v,w};head[u]=cnt;
e[++cnt]={head[v],u,0};head[v]=cnt;
}
int dis[MAXN];
const int INF=0x3f3f3f3f;
int n,S,T;
bool bfs(){
for(int i=1;i<=n;i++) dis[i]=INF;
queue<int> q;
q.push(S);dis[S]=0;
while(!q.empty()){
int u=q.front();q.pop();
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(e[i].w&&dis[v]>=INF){
dis[v]=dis[u]+1;
q.push(v);
}
}
}
return dis[T]<INF;
}
int dfs(int u,int limit){
if(u==T) return limit;
int ret=0;
for(int i=cur[u];i;i=e[i].nxt){
int v=e[i].to;
cur[u]=i;
if(dis[v]==dis[u]+1&&e[i].w){
int add=dfs(v,min(limit-ret,e[i].w));
e[i].w-=add,e[i^1].w+=add,ret+=add;
if(ret==limit) return ret;
}
}
return ret;
}
int dinic(){
int ans=0;
while(bfs()){
for(int i=1;i<=n;i++) cur[i]=head[i];
ans+=dfs(S,INF);
}
return ans;
}
无源汇上下界可行流
步骤:
将原图 \(G\) 转化为只有上界限制的 \(G'\)。
在 \(G'\) 上新建虚拟源点汇点 \(S,T\)。一条 \(G\) 上的边 \((u,v,low,up)\) 转化为 \(G'\) 上的 \((u,v,up-low)\)。\(in_u=\sum _v{e(v,u).low}-\sum _v{e(u,v).low}\).
若 \(in_u > 0\) ,从 \(S\) 到 \(u\) 连接上限为 \(in_u\) 的边。
若 \(in_u < 0\) ,从 \(u\) 到 \(T\) 连接上限为 \(-in_u\) 的边。
若 \(G'\) 能满流,则存在可行流。
有源汇上下界可行流
设 \(s,t\) 表示原图规定的源点、终点。注意 \(S,T\) 是建网络流之后的虚点。
步骤:
想办法转换成 无源汇上下界可行流。如果我们找到了一条可行流,那么相当于从 \(s\) 流出了很多,流到了 \(t\)。现在只要在原图上加一条 \((t,s,0,inf)\)。表示从 \(t\) 到 \(s\) 的下界为0,上界为 \(inf\) 的边。找这个新图的无源汇可行流,就可以找到原图的有源汇可行流。
有源汇上下界最大流
在跑完有源汇上下界可行流之后,从 \(s\) 到 \(t\) 跑残留网络上的最大流。注意要删除 \((t,s,0,inf)\) 这条边。
多源汇最大流
步骤:建虚点 \(S,T\)。\(S\) 向每一个源点连 \(inf\) 边,每一个汇点向 \(T\) 连 inf 边。跑普通最大流即可
#2 最大流建图方案
#3 最小割建图方案
跑完最大流之后。对于一个点 \(u\),只走不满流的边(剩余容量不为 \(0\)),能从 \(S\) 到
从 \(S\) 开始,只走不满流的边,能走到的 \(u\),都是属于 \(S\) 部。同理,
双向边的理解:省略了一个点
如图:
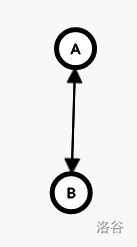
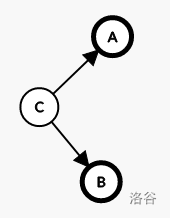
最小割
如何分化?https://www.cnblogs.com/Never-mind/p/8659982.html
最优选择: 文理分科 圈地计划
最基础的模型:只要看到 一个点,有两种选择。就要想到最小割。
每一个点 与 \(S\) 连的边的值为 “不取 \(S\) 的值的代价”。与 \(T\) 连的边的值为 “不取 \(T\) 的代价”。考虑一种选择方式,就是每一个点连的两条边,其中一条被割了之后。这个剩下的状态,如果 \(u\) 与 \(S\) 连通,表示 \(u\) 取 \(S\) 的值。你后面根据原题意要建什么虚点的时候,
最后跑最小割就是代价。
最小割的边权一般都是 代价,因为一般都是让 代价 最小,而不是 贡献 最小。所以你在建图的时候要把贡献转化为代价。方式就是,把所有的可能的贡献(哪怕这些贡献不能并存)都先加上,再减去最小的使图合法的代价。“不取A的代价”可以转化为“取A的贡献”
多个点,所有都取一个值 产生的贡献(&)怎么表示?
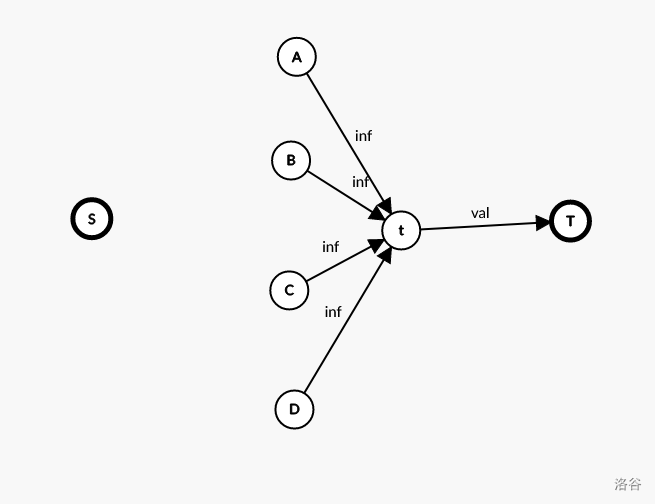
上图为 val=A、B、C、D同时取 T 能获得的贡献。解释:你想,如果ABCD中又任意一个点取了S,那个点就会与S连通,那么t也就会与S连通,所以val这个边一定会被割掉。割掉就表示不能加在答案里。
多个点,某些点取 \(S\),某些点取 \(T\),可以获得贡献怎么表示?
这种情况下,题目背景一般会有一些关于这两类点的性质。通常黑白染色可以达到一部分题目的要求。
多个点,只要某一个点就可以产生的贡献(|)怎么表示?
这个时候要把这个情况拆成几种互不关联的情况。
比如 A、B 只要任意一个取到了 \(T\) 就可以获得 val的贡献。
把它转化成两个情况:
-
A 取到 \(T\),可以获得 \(val\) 的贡献。
-
A 没取到 \(T\) 并且 B 取到 \(T\),可以获得 \(val\) 的贡献。
模板错误合集:
-
cnt初始值设为了 0
-
\(n\) 在主函数内重新定义了一遍,所以全局的没有被修改
-
for(int i=cur[i];i;i=e[i].nxt) -
当前弧优化是
cur[u]=i不是cur[i]=e[i].nxt很多题都过得了后一种,但是是错的!!!