Question

ABC336 F Rotation Puzzle

给出一个 \(H\times W\) 的矩阵，里面填有数字，有一种操作

• 选定一个 \((x,y)\) 交换 \((i+x,j+y)\) 和 \((H-i+x,W-j+y)\) 对于每一个 \(1\le i \le H-1,1\le j \le W-1\)

问，是否能经过 \(20\) 次以内的操作使得，最后的矩形变成 \((i,j)=((i-1)\times W+j)\)

Solution

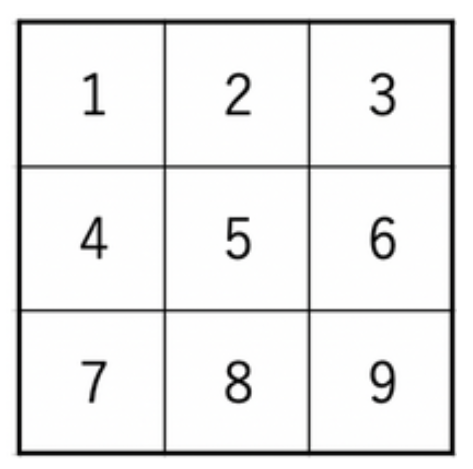
观察发现 \((i,j)=((i-1)\times W+j)\) 就是 \(1,2,3,\cdots\) 这样子下来

然后操作就是选一个顶点 \((x,y)\) 然后对于 \((H-1)\times (W-1)\) 的矩阵进行一次 "翻转" 操作

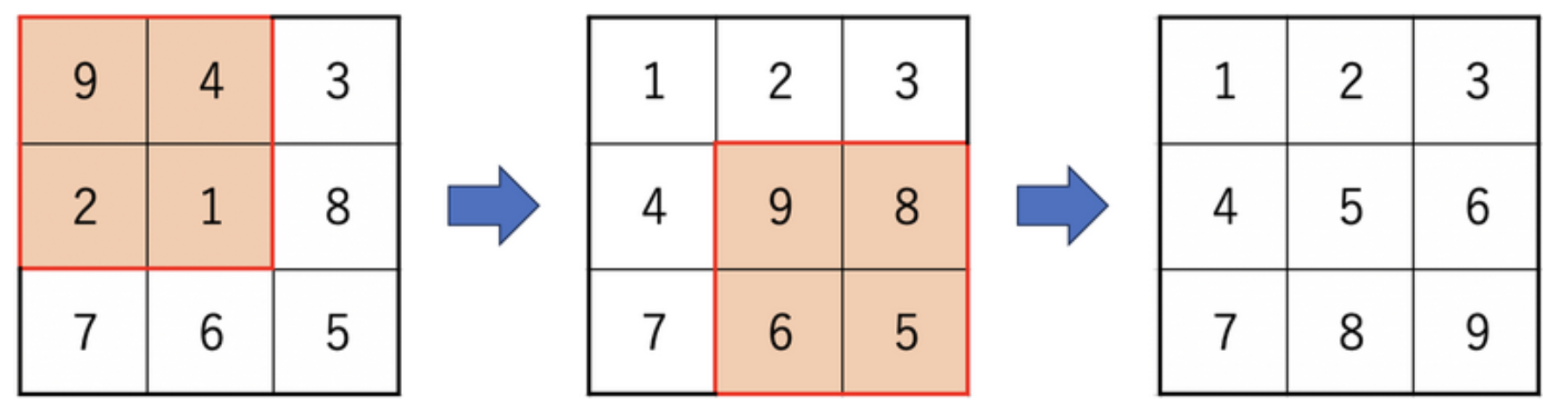
每次可以翻转的有四个选择 \((x,y)=(0,1),(1,0),(0,0),(1,1)\)

考虑暴力搜索，复杂度为 \(4^{20}=1099511627776\)

显然不符合，然后考虑折半搜索 \(4^{10}=1048576\)，复杂度降下来了，但是还是会超时

考虑到搜索的过程中有很多的重复元素，例如经过一次 \((0,0)\) 操作后再进行一次 \((0,0)\) 操作就没有意义了，所以有意义的操作次数是 \(3^{10}=59049\) ，用 BFS 比较实现去重

之后就是把一个矩阵对应一个数，对应到达这个矩阵状态的操作次数，从起点做一次 BFS，从终点做一次 BFS（就是折半枚举的常规操作）

Code

#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
typedef long long LL;
typedef vector<vector<int> > vee;
int n,m,ans=INF;
map<vee,int> mp1,mp2;

void F(int x,int y,vee& now){
    int cnt=0;
    for(int i=1;i<=(n-1);i++)
    for(int j=1;j<=(m-1);j++){
        swap(now[i+x][j+y],now[n-i+x][m-j+y]);
        if(++cnt>=(n-1)*(m-1)/2) return ;
    }
}

void bfs1(vee a){
    queue<vee> q;q.push(a);mp1[a]=0;
    while(!q.empty()){
        vee now=q.front(); q.pop();
        int stp=mp1[now];
        if(stp>=10) return;
        for(int x=0;x<=1;x++)
        for(int y=0;y<=1;y++){
            vee nxt=now;
            F(x,y,nxt);
            if(mp1.find(nxt)==mp1.end()){
                mp1[nxt]=stp+1;
                q.push(nxt);
            }
        }
    }
}

void bfs2(vee a){
    queue<vee> q;q.push(a);
    mp2[a]=0;
    while(!q.empty()){
        vee now=q.front(); q.pop();
        int stp=mp2[now];
        if(stp>=10) return;
        for(int x=0;x<=1;x++)
        for(int y=0;y<=1;y++){
            vee nxt=now;
            F(x,y,nxt);
            if(mp2.find(nxt)==mp2.end()){
                mp2[nxt]=stp+1;
                q.push(nxt);
            }
        }
    }
}

int main(){
    freopen("F.in","r",stdin);
    vee st;
    scanf("%d%d",&n,&m);
    st.assign(n+1,vector<int>(m+1,0));
    for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&st[i][j]);
    bfs1(st);

    int tot=0;vee ed(n+1,vector<int>(m+1,0));
    for(int i=1;i<=n;i++)for(int j=1;j<=m;j++) ed[i][j]=++tot;
    bfs2(ed);

    for(auto it=mp1.begin();it!=mp1.end();++it){
        if(mp2.find(it->first)!=mp2.end())
            ans=min(ans,it->second+mp2[it->first]);
    }

    if(ans==INF||ans>20)
        printf("-1\n");
    else 
        printf("%d\n",ans);
    return 0;
}