P10058 Reverse and Rotate题解

简单题意

一共 3 个操作：

• rev：将字符串翻转。
• > \(x\)：将后面 \(x\) 个字母移到前面。
• < \(x\)：将前面 \(x\) 个字母移到后面。

解法

解法一

看到 #1 到 #3 的范围可以打出暴力程序，按题意模拟，时间复杂度 \(O(n|S|)\)。
预计 \(30\) pts。

解法二

很明显，第二个操作和第三个操作有点像一个环，每个点就是字符串上一个字符。一开始头在第一个字符。

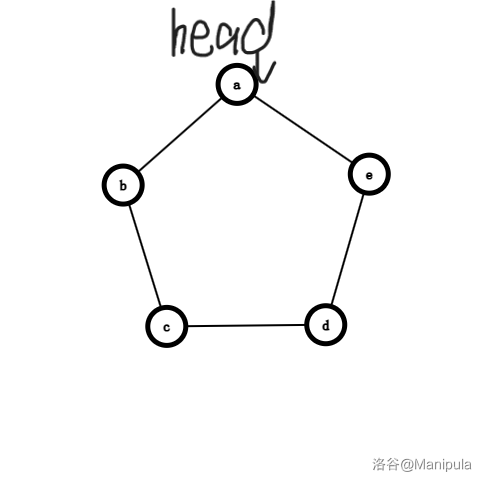
进行一次 > 2 后，头就变到了 d 上。

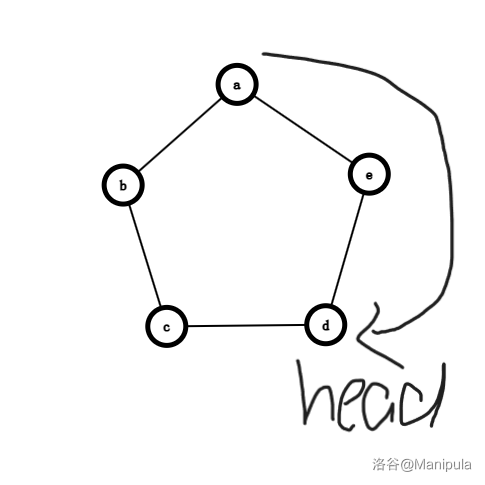
进行一次 < 2 也同理。

重点是 rev 操作，进行一次 rev 操作后，头变到了 c 上。

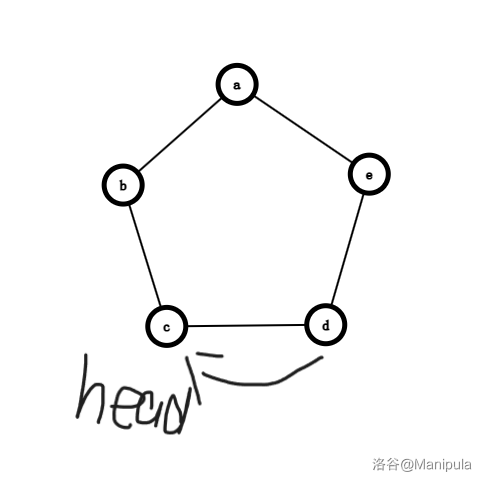
但此时再进行一次 > 2，却与上次不一样了。

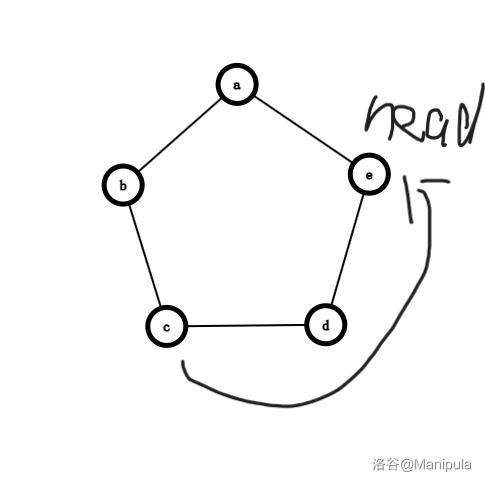
没错，他反过来了，所以这里可以用一个变量表示当前是正着走还是反着走，然后按上面说的方法模拟即可，若有不懂可以看看代码，时间复杂度 \(O(n)\)，预计 \(100\) pts。

Code

/*Code By Manipula*/
#include <bits/stdc++.h>
// #define Fileopen
// #pragma GCC optimize(2)
#define INF 0x7f7f7f7f
#define int long long
#define FOR(i, a, b) for (int i = (a); i <= (b); i++)
#define ROF(i, a, b) for (int i = (a); i >= (b); i--)
#define mst(arr, num) memset(arr, num, sizeof(arr))
#define max(x, y)((x) > (y) ? (x) : (y))
#define min(x, y)((x) < (y) ? (x) : (y))
#define swap(x, y) x ^= y ^= x ^= y
#define sqrt(n) pow(n, 0.5)
#define lowbit(x) (x & -x)
#define sort stable_sort
#define endl '\n'
using namespace std;
string str;
int T, head = 0, w = 1;
signed main()
{
	#ifdef Fileopen
		freopen(".in", "r", stdin);
		freopen(".out", "w", stdout);
	#endif
	cin >> str >> T;
	while (T--)
	{
		string opt; int x;
		cin >> opt;
		if (opt == "rev")head = (head + str.size() - w) % str.size(), w = -w;//转换方向，注意是 -w 不是 -1
		else
		{
			cin >> x; x %= str.size();//这里坑点，x 最大为 10^9，|s| 最大为 10^6，如果当前是减掉的话只加上一个|s|还是一个负数，所以先取模
			if (opt == ">")head = (head - w * x + str.size()) % str.size();
			else head = (head + w * x + str.size()) % str.size();
		}
	}
	//输出的时候要加上 w 而不是 1 啊
	for (int i = 0, k = head; i < str.size(); i++, k = (k + w + str.size()) % str.size())
		cout << str[k];
	return 0;
}