前言
今天考试考到这道题,挂惨了。
题意
有 \(n\) 道菜肴,编号为 \(1 \sim n\)。有 \(m\) 个条件,形如 \((i, j)\),表示菜肴 \(i\) 必须在菜肴 \(j\) 之前制作。需求出一个菜肴的制作顺序,满足:
-
在满足所有限制的前提下,\(1\) 号菜肴尽量优先制作。
-
在满足所有限制,\(1\) 号菜肴尽量优先制作的前提下,\(2\) 号菜肴尽量优先制作。
-
\(\dots\dots\)
-
以此类推。
如果无解,输出 Impossible!。
形式化
给定 \(n\) 个点,\(m\) 条边的有向图,需求出其拓扑序,满足在拓扑序合法的前提下,点 \(1\) 优先且点 $i(i \in |V|, i \ne 1) $ 在点 \(i - 1\) 优先的前提下优先。无解输出 Impossible!。
解法
首先给出一个错解,这东西是我考场胡的,但是可能对后面有帮助。
对于每一个点 \(x\),求出它往后的所有路径上经过的点的最小权值 \(mi_x\)(包括 \(x\))。然后使用堆进行拓扑排序,以 \(mi_x\) 为第一关键字,\(x\) 为第二关键字,就像这样:
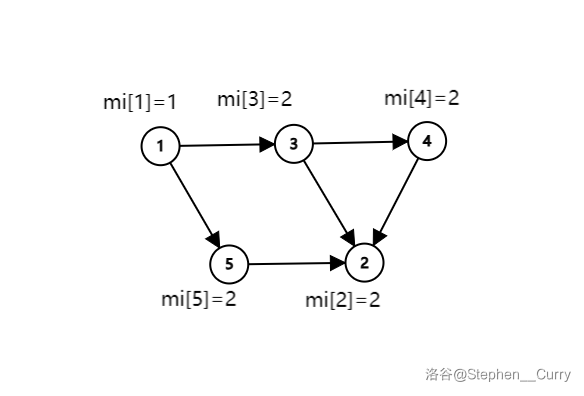
它的正确拓扑序为:\(1, 3, 4, 5, 2\)。
但是,它是错误的,不管是正确性还是时间。
我们来看这个例子:
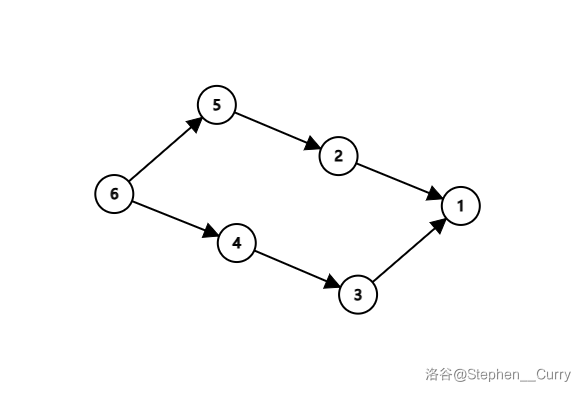
在这个图中,正确的拓扑序为 \(6, 5, 2, 4, 3, 1\),可这种方法跑出来的答案是 \(6, 4, 3, 5, 2, 1\)。可以发现,\(5\) 和 \(4\) 这两个点的 \(mi\) 是相等的,并且有公共的终点。这个时候,只要把两条路径中间的点调一下,这样贪心就是错误的。
关于时间,我采用的是 DFS,对于每个入度为 \(0\) 的节点,跑一遍 DFS,但是这样的最坏时间复杂度为 \(\Theta(\frac{n^2}{4})\),直接被卡飞。
我们可以对这个错解修改一下。
对于每个点 \(x\),它的子节点为 \(y_1, y_2, \dots, y_k\),在拓扑序中选择的先后顺序是这样的:将 \(y_1, y_2, \dots, y_k\) 往后的路径经过的点排序,然后按这些序列的字典序大小来选择。
按照刚刚的错解,错误的原因是多条路径上的最小值可能相等。那就一个一个从小到大比较啊,这样就是对的了。
这样做的朴素时间复杂度为 \(\Theta(n^2)\),但是可以使用 bitset 优化一下,可以将时间复杂度降为 \(\Theta(\frac{n^2}{w})\),算了一下单次大概 \(3 \cdot 10^7\) 的样子,数据组数小于等于 \(3\),那么就是 \(9 \cdot 10^7\),稍微卡一卡即可通过。
接下来讲时间复杂度正确的算法。
可以发现,我们刚才的分析都是正着分析的,但是这样是不好维护的,因为字典序小不一定是最优解。
那么我们倒着想。小的要在前面,那么大的就要在后面。在拓扑序合法的情况下,尽量把大的放在后面。那么这样就可以把小的数都尽量靠前。
那么,只需要在反图上跑字典序最大的拓扑序,然后反转一下即为答案。
字典序最大的拓扑序可以使用大根堆。
AC Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 5;
int t, n, m, in[N], IN[N], mi[N];
vector<int> e[N], ans;
void init()
{
ans.clear();
for(int i = 1; i <= n; i++)
e[i].clear();
memset(in, 0, sizeof(in));
memset(IN, 0, sizeof(IN));
// memset(mi, 0x3f, sizeof(mi));
return;
}
void topo_sort()
{
priority_queue<int> q;
for(int i = 1; i <= n; i++)
if(!in[i])
q.push(i);
int cnt = 0;
while(!q.empty())
{
int x = q.top();
q.pop();
cnt++;
ans.push_back(x);
for(auto y : e[x])
if(!--in[y])
q.push(y);
}
if(cnt != n)
{
cout << "Impossible!\n";
return;
}
reverse(ans.begin(), ans.end());
for(auto i : ans)
cout << i << " ";
cout << "\n";
return;
}
void solve()
{
cin >> n >> m;
init();
for(int i = 1; i <= m; i++)
{
int x, y;
cin >> x >> y;
e[y].push_back(x);
in[x]++;
}
// for(int i = 1; i <= n; i++)
// cout << mi[i] << " ";
// cout << "\n";
// for(int i = 1; i <= n; i++)
// for(int j = i + 1; j <= n; j++)
// if(!vis[i][j])
// {
// vis[i][j] = vis[j][i] = true;
// e[i].push_back(j);
// in[j]++;
// }
topo_sort();
return;
}
signed main()
{
// freopen("dishes.in", "r", stdin);
// freopen("dishes.out", "w", stdout);
cin >> t;
while(t--)
solve();
return 0;
}