[SDOI2017] 天才黑客
题目背景
SD0062号选手小Q同学为了偷到SDOI7012的试题,利用高超的黑客技术潜入了SDOI出题组的内联网的中央控制系统,然而这个内联网除了配备有中央控制系统,还为内联网中的每条单向网线设定了特殊的通信口令,这里通信口令是一个字符串,不同网线的口令可能不同。这让小Q同学感觉有些棘手,不过这根本难不倒他,很快他就分析出了整个内联网的结构。
题目描述
内联网中有\(n\)个节点(从\(1\)到\(n\)标号)和\(m\)条单向网线,中央控制系统在第\(1\)个节点上,每条网线单向连接内联网中的某两个节点,从\(1\)号节点出发经过若干条网线总能到达其他任意一个节点。每个节点都可以运行任意的应用程序,应用程序会携带一条通信口令,当且仅当程序的口令与网线的口令相同时,程序才能通过这条网线到达另一端的节点继续运行,并且通过每条网线都需要花费一定的时间。
每个应用程序可以在任意一个节点修改通信口令,修改通信口令花费的时间可以忽略不计,但是为了减小修改量,需要先调用一个子程序来计算当前程序的口令和网线的口令的最长公共前缀(记其长度为\(len\)),由于获取网线的口令的某个字符会比较耗时,调用一次这个子程序需要花费\(len\)个单位时间。
除此之外,小Q同学还在中央控制系统中发现了一个字典,每条网线的口令都是字典中的某个字符串。具体来说,这个字典是一棵\(k\)个节点(从\(1\)到\(k\)标号)的有根树,其中根是第\(1\)个节点,每条边上有一个字符,字符串\(S\)在字典中当且仅当存在某个点u使得从根节点出发往下走到u的这条路径上的字符顺次拼接构成\(S\)。
现在小Q同学在\(1\)号节点同时开启了\(n-1\)个应用程序,这些应用程序同时运行且互不干扰,每个程序的通信口令都为空,他希望用最短的时间把这些程序分别发送到其他节点上,你需要帮小Q同学分别计算出发送到第\(i(=2,3,\dots ,n)\)个节点的程序完成任务的最短时间。
输入格式
第一行是一个正整数\(T\),表示测试数据的组数,
对于每组测试数据,第一行是三个整数\(n\) , \(m\) , \(k\),分别表示内联网的节点数、内联网的网线条数、字典树的节点数,
接下来\(m\)行,每行包含四个整数\(a_i,b_i,c_i,d_i(1 \leq a_i,b_i \leq n , 0 \leq c_i \leq 20000 , 1 \leq d_i \leq k)\),表示沿着这条网线可以从第\(a_i\)个节点花费\(c_i\)个单位时间到达第\(b_i\)个节点,网线的口令是由从字典树的根到\(d_i\)这个点的路径上的字符顺次拼接构成的字符串(可能为空),需要注意的是这个内联网可能有自环和重边,
接下来\(k-1\)行,每行包含三个整数\(u_i,v_i,w_i(1 \leq u_i,v_i \leq k , 1 \leq w_i \leq 20000)\),表示字典树上有一条\(u_i \rightarrow v_i\)的边,边上有字符\(w_i\),保证给出的边构成一棵以\(1\)为根的有根树,并且每个点连出去的边上的字符互不相同。
输出格式
对于每组测试数据,输出\(n-1\)行,第\(i\)行表示发送到第\(i+1\)个节点的程序完成任务的最短时间。
样例 #1
样例输入 #1
1
4 4 6
1 2 2 5
2 3 2 5
2 4 1 6
4 2 1 6
1 2 1
2 3 1
3 4 1
4 5 2
1 6 2
样例输出 #1
2
7
3
提示
【样例解释】
对于样例,从\(1\)到\(3\)的一条可行路径是\(1 \rightarrow 2 \rightarrow 3\),所需时间是\((2 + lcp(``" , ``1112")) + (2 +lcp(``1112" ,``1112")) = 8\),但这条路径不是最优的,最优路径是\(1 \rightarrow 2 \rightarrow 4 \rightarrow 2 \rightarrow 3\),
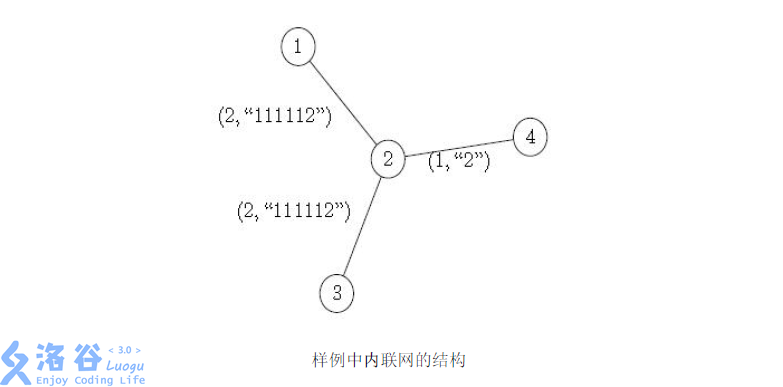
对于\(100\%\)的数据\(T \leq 10\),\(2 \leq n \leq 50000\),\(1 \leq m \leq 50000\),\(1 \leq k \leq 20000\),保证满足\(n>5000\)或\(m > 5000\)的数据不超过\(2\)组。

题解
由于问题仍然是一个最短路,考虑dijkstra.
用点跑最短路显然是不行的,考虑跑边的最短路。对于相接的两条边 \(x,y\),他们的边权为 \(c_y+dep(lca(x,y))\),dep 和 lca 都指在字典树上的。设到达某条边 \(x\) 最小权值为 \(ds_x\),那么把所有点 \(u\) 的入边 \(p\) 到出边 \(q\) 后出边 \(q\) 应该用 \(ds_p+c_q+dep(lca(p,q))\) 来更新。考虑优化建图直接跑
法一
考虑如何去处理 \(dep(lca(p,q))\)。下面设第 \(i\) 个点的dfs 序为 \(dfn_i\) 且 \(dfn_p<dfn_q\),\(h_i\) 为 dfs 序为 \(i\) 的和 dfs 序为 \(i+1\) 的两个串的最长公共前缀,那么 \(dep(lca(p,q))\) 等于 \(min_{i=dfn_p}^{dfn_q-1}h_i\)。对每个点的入边出边建出虚树。考虑优化建图。对于虚树的某个点,\(i\),用前缀和建图使得入边到出边的 dfn 跨过他的都连一条 \(h_i\) 的边。直接跑 dijkstra 即可。
法二
自己胡的,lg题解区好像没有这种做法。
考虑模拟 dijkstra 的过程。现在要找到距离最小的边。考虑对每个点维护出经过这个点后距离 1 最小的边。
\(dep(lca(p,q))=\frac12 (dep_p+dep_q-dis(p,q))\),那么此时入边 \(p\) 到出边 \(q\) 可以表示成 \(-\frac12 (dis(p,q)-dep_p-2ds_p-2c_q-dep_q)\),把后面那些东西当作点权,用直径的性质去维护每个点距离最小的出边,用个堆维护每个点的出边的最小值,模拟 dijkstra 跑就行了。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=50005;
const LL INF=1e18;
int T,n,m,k,a[N],b[N],c[N],d[N],dep[N],idx,vs[N],in[N],ls[N],lg[N],ans[N],dfn[N],to[N];
LL h[N];
pair<int,int>st[20][N],tr[N<<2],p[N],sh[N];
vector<int>g[N];
struct node{
int v,d;
bool operator<(const node&n)const{
return d>n.d;
}
};
priority_queue<node>q;
void dfs(int x)
{
st[0][dfn[x]=++idx]=make_pair(dep[x],x);
for(int v:g[x])
dep[v]=dep[x]+1,dfs(v),st[0][++idx]=make_pair(dep[x],x);
}
int lca(int x,int y)
{
if(dfn[x]>dfn[y])
swap(x,y);
int k=lg[dfn[y]-dfn[x]+1];
return min(st[k][dfn[x]],st[k][dfn[y]-(1<<k)+1]).second;
}
int dis(int x,int y)
{
return dep[x]+dep[y]-2*dep[lca(x,y)];
}
LL ask(int x,int y)
{
if(!x||!y)
return -INF;
return dis(d[x],d[y])+h[x]+h[y];
}
pair<int,int>mge(pair<int,int>u,pair<int,int>v)
{
if(!u.first||!v.first)
return make_pair(u.first|v.first,u.second|v.second);
pair<int,int>k=u;
if(ask(v.first,v.second)>ask(k.first,k.second))
k=make_pair(v.first,v.second);
if(ask(u.first,v.first)>ask(k.first,k.second))
k=make_pair(u.first,v.first);
if(ask(u.first,v.second)>ask(k.first,k.second))
k=make_pair(u.first,v.second);
if(ask(u.second,v.first)>ask(k.first,k.second))
k=make_pair(u.second,v.first);
if(ask(u.second,v.second)>ask(k.first,k.second))
k=make_pair(u.second,v.second);
return k;
}
void upd(int o,int l,int r,int x,pair<int,int>u)
{
if(l==r)
return tr[o]=u,void();
int md=l+r>>1;
if(md>=x)
upd(o<<1,l,md,x,u);
else
upd(o<<1|1,md+1,r,x,u);
tr[o]=mge(tr[o<<1],tr[o<<1|1]);
}
pair<int,int>ask(int o,int l,int r,int x,int y)
{
if(x<=l&&r<=y)
return tr[o];
int md=l+r>>1;
pair<int,int>k=make_pair(0,0);
if(md>=x)
k=mge(k,ask(o<<1,l,md,x,y));
if(md<y)
k=mge(k,ask(o<<1|1,md+1,r,x,y));
return k;
}
void build(int o,int l,int r)
{
if(l==r)
return tr[o]=make_pair(to[l],to[l]),void();
int md=l+r>>1;
build(o<<1,l,md);
build(o<<1|1,md+1,r);
tr[o]=mge(tr[o<<1],tr[o<<1|1]);
}
void getnw(int x)
{
pair<int,int>u=ask(1,1,m,ls[x-1]+1,ls[x]),v=p[x],k=make_pair(u.first,v.first);
if(ask(u.first,v.second)>ask(k.first,k.second))
k=make_pair(u.first,v.second);
if(ask(u.second,v.first)>ask(k.first,k.second))
k=make_pair(u.second,v.first);
if(ask(u.second,v.second)>ask(k.first,k.second))
k=make_pair(u.second,v.second);
if(k.first&&k.second)
q.push((node){k.first,-ask(k.first,k.second)>>1}),sh[x]=make_pair(k.second,k.first);
}
void add(int x,int c)
{
ans[b[x]]=min(ans[b[x]],c);
upd(1,1,m,in[x],make_pair(0,0));
vs[x]=1;
h[x]=-2LL*c-dep[d[x]];
p[b[x]]=mge(p[b[x]],make_pair(x,x));
if(!sh[a[x]].second||x==sh[a[x]].second)
getnw(a[x]);
getnw(b[x]);
}
signed main()
{
for(int i=2;i<N;i++)
lg[i]=lg[i>>1]+1;
scanf("%d",&T);
while(T--)
{
memset(vs,idx=0,sizeof(vs));
memset(ans,0x7f,sizeof(ans));
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;i++)
g[i].clear(),p[i]=sh[i]=make_pair(0,0);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d%d",a+i,b+i,c+i,d+i);
g[a[i]].push_back(i);
}
for(int i=1,k=0;i<=n;i++)
{
for(int j:g[i])
to[in[j]=++k]=j;
ls[i]=k;
}
for(int i=1;i<=k;i++)
g[i].clear();
for(int i=1,u,v;i<k;i++)
scanf("%d%d%*d",&u,&v),g[u].push_back(v);
dfs(1);
for(int i=1;i<=m;i++)
h[i]=-2*c[i]-dep[d[i]];
for(int i=1;i<=lg[idx];i++)
for(int j=1;j+(1<<i)-1<=idx;j++)
st[i][j]=min(st[i-1][j],st[i-1][j+(1<<i-1)]);
build(1,1,m);
for(int i=1;i<=m;i++)
if(a[i]==1)
add(i,c[i]);
while(!q.empty())
{
int v=q.top().v,dis=q.top().d;
q.pop();
if(vs[v])
continue;
add(v,dis);
}
for(int i=2;i<=n;i++)
printf("%d\n",ans[i]);
}
}