Robot Breakout(CF1196C)

思路

这道题因为平面极大，暴力枚举每个点肯定会超时。所以，我们不妨从机器人出发。

我们可以枚举每个机器人可以执行的操作：

1. 位置从 \((X_i,Y_i)\) 变为 \((X_i-1,Y_i)\)，即向左走。

2. 位置从 \((X_i,Y_i)\) 变为 \((X_i,Y_i+1)\)，即向上走。

3. 位置从 \((X_i,Y_i)\) 变为 \((X_i+1,Y_i)\)，即向右走。

4. 位置从 \((X_i,Y_i)\) 变为 \((X_i,Y_i-1)\)，即向下走。

如果一个机器人执行不能执行操作 \(4\)，那么下图的蓝色区域为该机器人的行动范围：

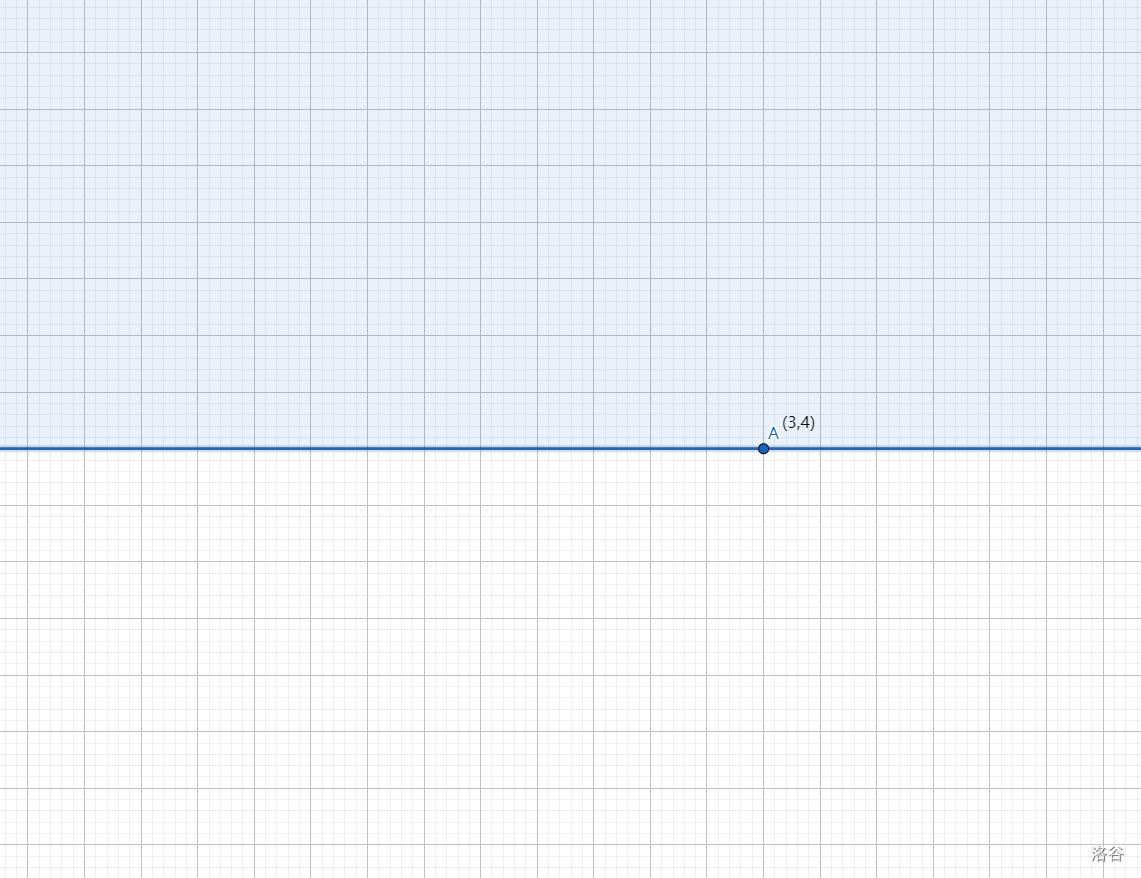
那么很多个机器人，它们的集合点就应该是这些区域的相交处：

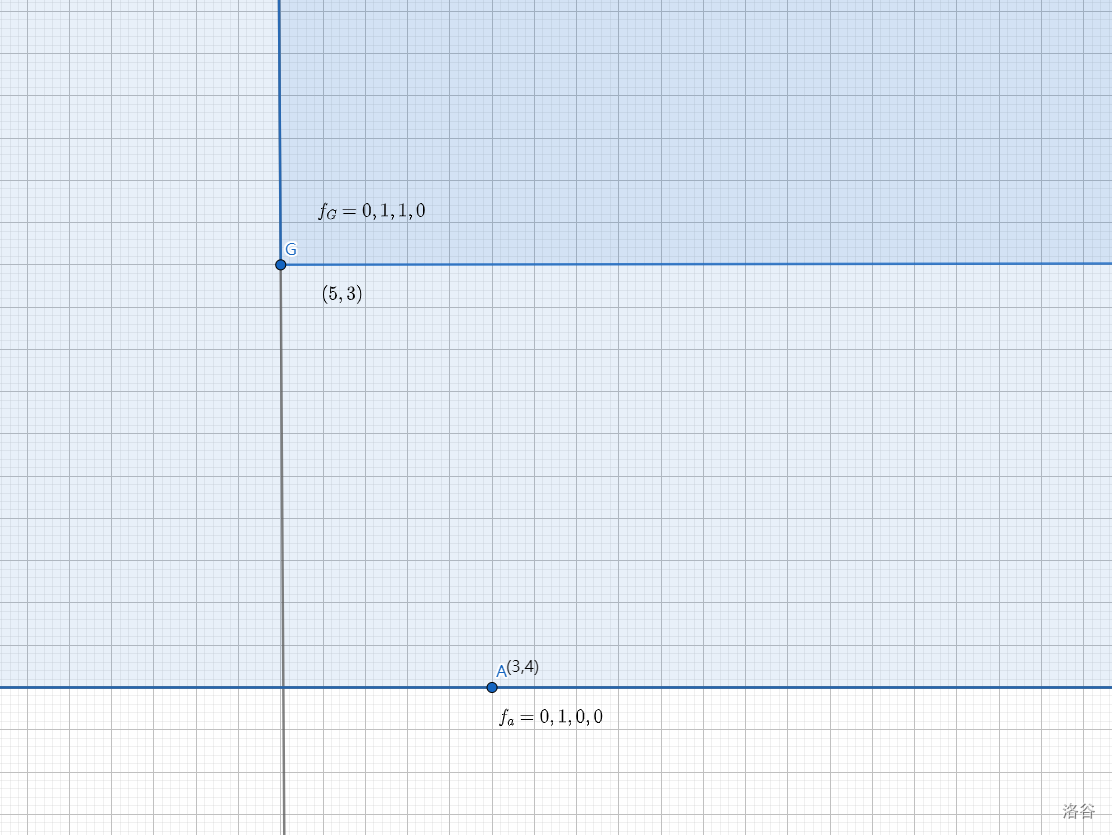
我们便可以用变量 \(up,down\) 储存集合点 \(y\) 坐标的上下界，\(left,right\) 储存集合点 \(x\) 坐标的上下界。

如果当前机器人，无法下行，则 \(down=\max(down,a_iy)\)；

如果当前机器人，无法左行，则 \(left=\max(left,a_ix)\)；

如果当前机器人，无法下行，则 \(up=\min(up,a_iy)\)；

如果当前机器人，无法左行，则 \(right=\min(up,a_ix)\)；

Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 1e5 + 5;
int n;
struct bot {
	int x, y;
	int f[5];
} a[MAXN];
int r=1e5, up=1e5, l=-1e5, down=-1e5;
void work(){
	r=1e5, up=1e5, l=-1e5, down=-1e5;
	scanf("%lld", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%lld", &a[i].x);
		scanf("%lld", &a[i].y);
		for (int j = 1; j <= 4; j++) {
			scanf("%lld", &a[i].f[j]);
		}
		if(a[i].f[1]==0){//不能向左走
			l=max(l,a[i].x);
		}
		if(a[i].f[2]==0){//不能向上走
			up=min(up,a[i].y);
		}
		if(a[i].f[3]==0){//不能向右走
			r=min(r,a[i].x);
		}
		if(a[i].f[4]==0){//不能向下走
			down=max(down,a[i].y);
		}
	}
	if(l<=r&&down<=up) printf("1 %lld %lld\n",l,down);
	else printf("0\n");
}
signed main() {
	int q;
	scanf("%lld",&q);
	while(q--){
		work();
	}
	return 0;
}