AtCoder Beginner Contest 复盘合集
2023.12.6 ABC312 VP(OI赛制)
这次的ABC相对比较难:红橙黄黄蓝绿绿,Ex(蓝)
A
B
稍微麻烦一点。
C
很水,直接Sort一遍即可。
D
稍微思考,可以得出一个DP,准确来说不太像DP
【警钟长鸣】我非常的弱智,\(n <= 3000\) 赛时写成1000。因为OI赛制,所以很弱智的挂分。
赛时因为无脑写压维被卡,换成二维即可过掉。
【坑点】闲着没事开滚动数组。
E
其实我一开始也是认为要维护每一个面,也就是每一个坐标,然后进行前缀和或者差分,但是觉得很复杂。后面突然间想到,其实暴力即可。为什么?因为如果你 \(n\) 个输入都直接遍历他的每一个 \(x,y,z\) 都是没有问题的。理论上会达到 \(n * 100^3\) 肯定会TLE。但是题目中有一个条件 每一个长方体的体积没有相交。意味着我们最多只会遍历 \(100^3\) 。非常nice。然后存到一个三维的数组当中后:
我们可以通过六个面来看周围是不是其他长方体,但是我们发现如果你往 \((x+1,y,z)\) 和 \((x-1,y,z)\) 是等价的。这是啥意思呢?因为你的 \(x-1\) 可以由 \(x-1\) 来判断它的 \(x+1\)(也就是 \(x\))来解决。
于是呢我们就可以通过三个if来判断。我真聪明。
然后再用一个set维护即可。
时间充裕:$O(100^3\times \log n) $ 非常轻松水了一道蓝。。
准确来说这应该是绿吧。
F
赛后发现巨水。可以说是思考10s,码量2min,调1.5h
甚至还请了何竺凌来帮我调。。。
最后发现的问题是在:
for(int i =1;i <= m;i++){
f[i] = max(f[i],f[i-1]);
}
整体思路是算t=0的部分的答案,和t=1,t=2的答案,然后最后组合在一起即可。
但是会发现如果需要选6个,但是只有2个可以选,那么会出现中间是空的,无法组合 ,这样,我们只需要把f数组渲染一遍即可。
总结:
这次其实F挺水的。大概是正常的D。赛时没切F主要是时间不够,而且一直认F是很难的。所以没搞F。然后D耽误了一点时间,总体来说发挥不太好。(OI赛制嘛,一般来说正常AT我都是罚时吃饱。。
2023.12.9 ABC301 VP(OI赛制)
A:
签到,从头开始遍历,记录A和T的数量,如果相等,判断一下最后一个是什么如果是A则输出T,如果是T则输出A
B
签到,模拟即可
link
C
签到,依次遍历,如果存在不是 atcoder 这几个字符之外的有不同数量,那么就是不合法。
如果这些字符数量超过两个字符串的 @ 之和,那么也是不合法的。简单实现:
D
非常签到,很容易想到贪心,能取得就取,从前往后依次遍历。
先记录一遍如果所有 @ 都为 0 的情况下是多少,也就是最小二可能,然后
注意了:他这个地方是按照正序输入二进制的,所以应该是从前往后遍历才能取到尽可能大的值。
PS:【警钟长鸣】赛时挂掉的原因是位运算左移没有将1改成1ll,导致等于没有开long long。挂分/
E
是一道思维量少,码量大的题目。
由于猴子的数量很小,是18以内,所以我们只需要预处理逐个猴子之间的距离。大概是我们团队SFLS校园的一个弱化版。甚至只用BFS不用Dij,后面直接转移一下就可以了(类似Dp)但是因为下标(状压位运算的遍历范围)有些问题,调了很久,感谢@2020luke同学帮忙调过!!
一些位运算(状压)的细节,例如遍历到多少这些一定不能算少也不能算多。因为算少肯定影响结果,算多可能会导致重复计算或者是一些奇奇怪怪的东西出现,就是去了一些比n大的猴子。。。(当时没有考虑仔细,没有想到如果算多了会怎么样,比较马虎的大概设置了边界。zsy帮忙调了边界后过掉了。
稍微有点屎山。
总结:
这次是切了ABC,OI赛制比较难受,所以有些细节没有搞定,然而码量大的有没有码出来,码量小的又弱智丢分。所以下次还是要更加细心,不要因小失大。
2023.12.10 ABC321 VP(IOI赛制)
A
逐个拆位,然后与上一个比较即可
B
维护一下sum,最大值,最小值,枚举k进行答案的计算,做完了
C
发现\(n\)很小,可以打表。\(O(1)\)
写完发现题解区全是打表
D
先排序。然后做一遍前缀和。
枚举A,然后二分B,找到前面使用s,后面使用P的地方,然后进行\(O(1)\)计算。
F
拿一个球,拿走一个球,发现时间复杂度允许 \(O(qk)\)。于是,我们可以使用 DP 来记录和为 \(i\) 时的数量。
如果是新增,那么每一个 \(DP_i += DP_{i-x}\)。注意要倒序,因为前面的做完不能影响到后面。
如果是减少,那么每一个 \(DP_i -= DP_{i-x}\)。但是这个地方是需要正序进行,因为一个球是由 \(i-x\) 来的,所以应当减去他没有这个球的时候的数量。然后后面的却要调用前面的来,也就是说,\(DP_i\),一定是从 $DP_{i-x} 转移来才能为 \(DP_{i+x}\) 的转移带来可以减少的数。
核心代码就是分别讨论,套一个for循环,然后进行上述的逐一转移。
注意的细节:取模的时候减法要 + mod % mod
加法就是正常的 % mod
Ps:取模的地方要注意了。
2023.12.12 ABC320 VP(IOI赛制)
A
【警钟长鸣】别用pow!!不知道为什么,用pow会精度损失,所以直接手写
link
B
直接 \(O(n^3)\) 暴力枚举即可。
link
C
一开始有一些理解错误。
其实他的意思就是每一个字符串的 t 是不同时间,所以不妨讲每一个字符串直接复制三倍,然后暴力枚举。\(O(27 \times M^3)\)
link
D
我们可以利用已经知道的(1,1)的坐标,然后bfs广度延申,将所有的点都搜出来。时间复杂度足够 \(O(m)\)
【坑点】要建立双向边,因为如果可以从 a 推向 b,也可以从 b 推向 a,然而,x和y要做一下取反。于是就搞定了。
link
E
可以针对 n 个人进行处理。用一个set维护,然后每一次找到最小值,不断往后二分下一个点,如果存在的话,那么ans加上那个,否则直接break
一开始用数组手写二分。可能细节的问题,卡了很久,最后重构就AC了。时间复杂度是 \(O(m \log n)\)
link
2023 12.12 ABC279 VP(OI赛制)
A
老师都说很弱智,所以很弱智。
link
B
查找子串?对,Kmp,板子。。 但是实际上 \(n=100\) 直接暴力枚举两个字符串的左端点,遍历一遍,结束。
link
C
很显然,直接存储每一列,sort一遍即可。
link
以上就是我赛时切的 很弱智。。。没错,两个小时干了三个红题。
D
这是一道黄。但我赛时没有切。很显然,取最小值,因为g在一个地方是乘,另一个地方是除。显然是一个抛物线。那么?三分!!正好前几天学了三分。
然而我两个小时都在调这一题。。。
总结出来,有一玄学的点:
改完之后不仅能使你的样例过不了,还可以使你成功AC!!
【侯森凯学长之邪教】不会二分边界怎么办?很好办:
if(r <= l+5) printf("%.10lf",min({check(l),check(l+1),check(l+2),check(l+3),check(l+4),check(l+5)}));
愉快的解决掉了不会二分边界的问题。
Ps:因为翻译比较简练,所以不知道g是整数!!瞎搞了半个多小时。然而老师亲切的提醒了后,还是一直挂着。于是一只眼睛调D,一只眼睛看E题思路///最后是两个都没有完成啊啊。
link
E
@2020luke 因为赛时切了这题(绿)跟我炫耀了一个小时。/
是一个Dp表示状态。。
需要预处理:
- 每一个点到最后在什么位置(没有删除操作)。
然后我们可以进行 \(O(m)\) 的for循环。设 \(DP_i\) 表示的是到 \(i\) 个操作的时候 \(1\) 点的位置。
本题难点主要在于需要想到几个数组互相映射出来的。
F
其实想了想并不难的。
很巧妙地运用了并查集。
很正常的存一个并查集,我们把每一个球和箱子都设做一个并查集中的点。
然而,合并的时候直接合并嘛。哪有那么简单。想到合并之后有可能还会有其他点的加入,这样就会发生错误。
所以,我们在合并了两个箱子之后,原来被合并的那个箱子显然是不能再用的,于是我们可以新开一个箱子。然后用一个数组映射一下,记录他实际是什么箱子。
在很多个数组的映射中,再套上一个并查集,结束。注意一下细节。考虑到箱子可能很多个所以我们要开三倍的空间足够我们折腾。
膜拜一下学长,场切EF!!
2023.12.14 ABC278 VP(OI赛制)
A
没有场切很弱智,没有考虑到 \(k > n\) 的情况。
luke因为ABCDE都没挂分,又在炫耀。。。
link
B
因为时间复杂度十分充裕,所以直接枚举答案,进行判断即可。场切
link
C
发现数据范围是\(1e9\)无法当下标来存,所以直接想到set维护时间复杂度 \(O(q \log n)\) 可以过掉。在过程中直接二分即可。实际上可以使用“高科技”find函数一键解决。/场切
link
D
其实做法启示于线段树中的“Lazy-tag”就是等到要查询的时候再来判断是否要更新,大大减少了清空的时间复杂度。在每一个数开一个结构体,存一下最后修改的时间,如果发现在这个时间后有操作进行了清空,于是再给他做清空。
场切
link
E
只需枚举一下每一个hw的矩阵的左上角的下标,然后类似滑动窗口的做法,逐个往右移动,然后只需要稍微修改维护一下边界的加减即可。因为 \(k\) 是 \(300\) 级,所以直接开个数组可以统计个数,所以能够实时维护ans答案/
场切
link
F
其实并不难,不知道为什么考场没有搞出来,没了一个小时。
实际上是一个状压Dp,想到了,但不知道具体怎么搞。我们可以设\(DP_{i,j}\) 代表\(i\) 这个状态下面以 \(j\) 这个字符出结尾的能否必胜。然而,\(n<=16\)级的数据完全可以状压瞎枚举。通过转换一下,这个必胜,那么如果到达他之后的一个点那就是必输。很显然的博弈论嘛
最后只要有一个必胜,那就是first胜利,毕竟他是主动权的嘛。如果一个没有,那么就是Second 胜利。
感觉一有点博弈论就不行了。 场切不过黄,太弱了,下次加油!!
link
2023.12.16 ABC333
A
主打个弱智
link
B
第一眼:那么水,第二眼:WA!,第三眼AC了。抽象没有注意到是环,【不看题】+1
link
C
全场中最难的,我想到了贪心,我想到了打表,我想到了DP,我想到了预处理,但是我没有想到暴力,原来是暴力就可以过了也。菜就菜,别狡辩
link
D
非常简单的一眼题目。只用维护 \(1\) 的子树大小之和,然后减去最大子树的的大小,结束。。
link
E
稍微一丢丢的思考量,边想边写=AC。因为尽量保持每时每刻的背包重量最小,所以不妨在打一个怪兽前拿一个里此时最近的药(假设你可以穿越时空往回走。那么我们可以用一个stack维护。在遍历 \(1-n\) 的时候,如果是 \(1\) 那么就在stack里面添加 \(x\),然后,到了操作 \(2\) 的时候在栈里弹出栈顶的(肯定是目前情况最近的)。注意:在维护栈的时候要使用pair,这样才能维护到你之前取的药是第几个。然后如果这个地方取了药,那么前缀和++,打怪兽这个地方--,于是跑一边前缀和,实时求最大值即可。
话说,这玩意最大值最小是不是可以二分?,但好像又不可以,所以说:最大值最小,最小值最大不一定是二分,有可能是贪心,暴力。
2023.12.22 ABC265 VP(OI赛制)
A
注意细节,y 有可能更不划算。
B
OI 赛制 WA 了,题目描述不是特别清楚,t = 0 的时候也是合法的。
C
过了,随便一个while循环实时维护即可
D
读题假了,要求区间 \(x ~ y-1\) ,我搞成 \(x ~ 任意\) 。成功WA 掉 hack点,赛时数据竟然都能过!!!
link
E
首先,这一题很显然是一个 Dp。
考虑如何转移状态,因为一开始的坐标是 \((0,0)\)。
发现最后的坐标是 \((A\times i + C \times j + E \times k,B\times i + D \times j + F \times k)\)。如果是统计最后的种类的话,那么就比较简单,枚举 \(i\),\(j\) 和 \(k\)。但是题目要求的是方案数,所以我们可以用一个三维 Dp,转移一下 \(i\),\(j\) 和 \(k\) 时的方案数,很容易想,可以从 \(i-1\),\(j-1\) 和 \(k-1\) 分别转移。所以后面枚举 \(i\),\(j\) 和 \(k\) 只需要累加其 Dp 状态即可。
不可行的方案用 map 存储特判掉即可。
上代码:
赛时切了。
F
有点懵,目前未解决,过两天琢磨琢磨再补上。
现在懂了。。。
直接把我的题解copy上来咯。
考虑 Dp,可以先设 \(dp_{i,j,k}\) 为前 \(i\) 维,\(r\) 到 \(p\) 所累积的距离为 \(j\),\(r\) 到 \(q\) 累计的距离是 \(k\)。于是 \(dp_{i,j,k}\) 从 \(dp_{i-1,j-|r_i-p_i|,k-|r_i-q_i|}\) 转移来。
因为有绝对值,所以得要进行分类讨论。具体情况如下。
放上这张图片:
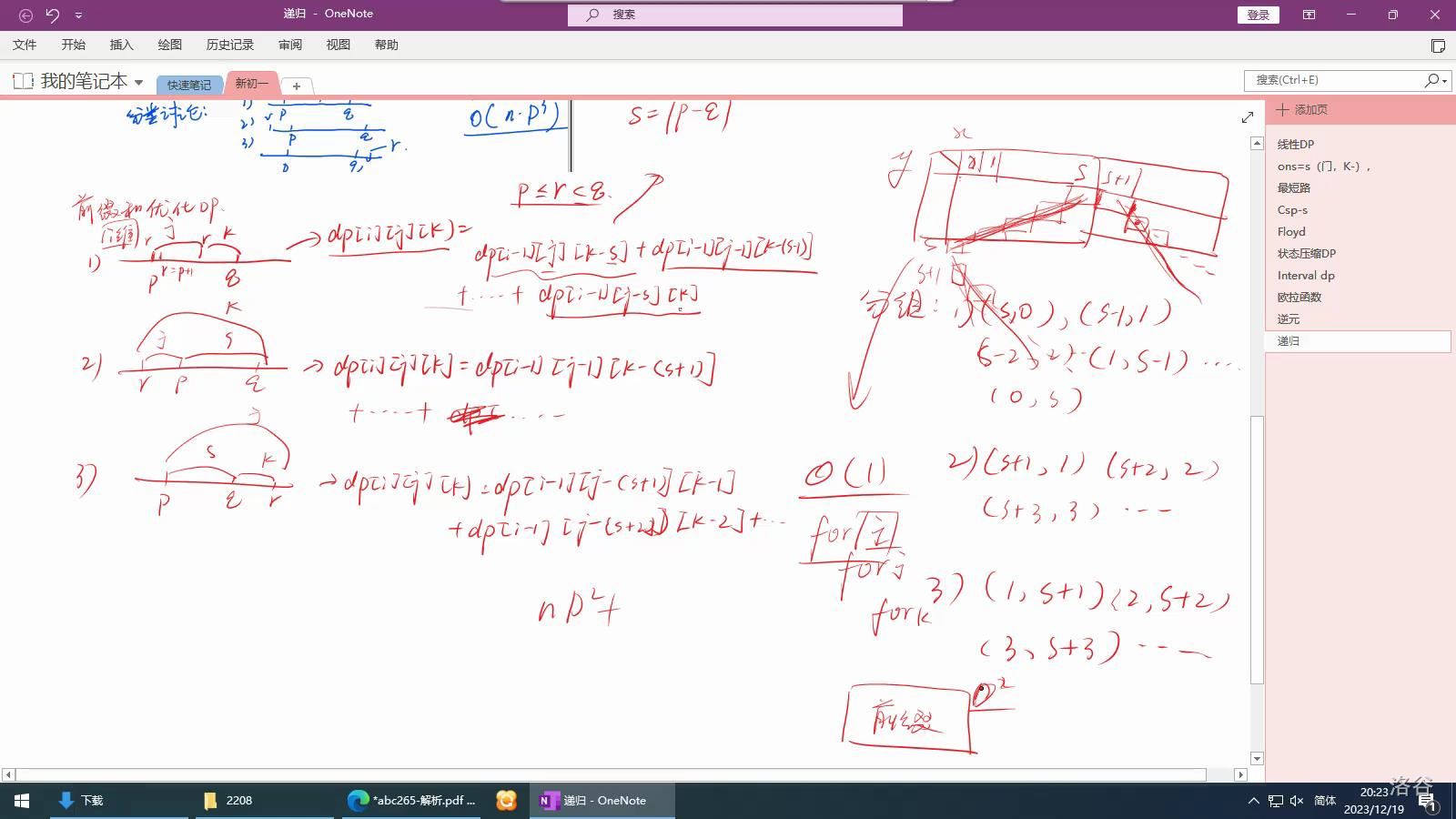
注:图片中的文字均有在下文提及。主要还是为了展现教练的灵魂画图。
设:\(x = |p_i - q_i|\)。
不妨先对正常的情况尽心分类讨论一下。
- 第一种情况:\(r_i\) 在 \(p_i\) 与 \(q_i\) 中间。\(dp_{i,j,k} = dp_{i-1,j,k-x} + \cdots + dp_{i-1,j-x,k}\)。
- 第二种情况:\(r\) 在 \(q_i\) 和 \(p_i\) 的左边。\(dp_{i,j,k} = dp_{i-1,j-1,k-x-1} + dp_{i-1,j-2,k-x-2} + \cdots\)。
- 第三种情况:\(r\) 在 \(q_i\) 和 \(p_i\) 的右边。\(dp_{i,j,k} = dp_{i-1,j-x-1,k-1} + dp_{i-1,j-x-2,k-2} + \cdots\)。
但这是一个 \(O(n D^3)\) 的暴力,无法通过。所以考虑如何优化这个 Dp,想到前缀和优化。
还是像刚才一样,分类讨论前缀和,因为情况的不一样,我们会发现第二第三种情况其实比较类似的,所以我们可以分成两个前缀和来写。
-
第一种前缀和:包含着上述暴力中的第一种情况。由于我们发现 \(j+k\) 一直是一个数,显然这是一个反着的对角线,可以抽象的理解就是从右上角连向左下角,说白了,就是主对角线的垂直对角线。\(qzh_{j,k}\) 来表示 \(dp_{i-1,0,k+j} + \cdots + dp_{i-1,j,k}\) 这条对角线,记录他的累加和,到最后状态转移计算中直接调用就可以咯。
-
第二种前缀和:包含着上述暴力中的第二和第三种情况。由于 \(j-k\) 是不变的,所以是一条平行于主对角线的线,可以理解为第一种前缀和的垂直的线段。那么我们显然需要再开一个前缀和数组来记录,毕竟方向都是不一样的,怎么能够共用呢!于是,定义:\(qzh2{j,k}\) 从这一条线开始连到 \(dp_{i-1,j,k}\) 的值。第二种情况中:\(dp_{i-1,s,0}\) 开始,第三种情况中:\(dp_{i-1,0,s}\) 开始。
这只不过是更加严谨的说法罢了。
所以呢?
做完了,只需要在状态转移的时候压缩掉一个 \(O(D)\) 的时间复杂度。
我认为吧,其实前缀和的优化并不是特别难,说白了就相当于预处理一些东西而已,但是这种解法确实也是难想,只不过是教练带着才做出来。实际上这一题的难度还是有的!
link。
2023.12.24 ABC334
开题四分钟竟然拿到rk5/
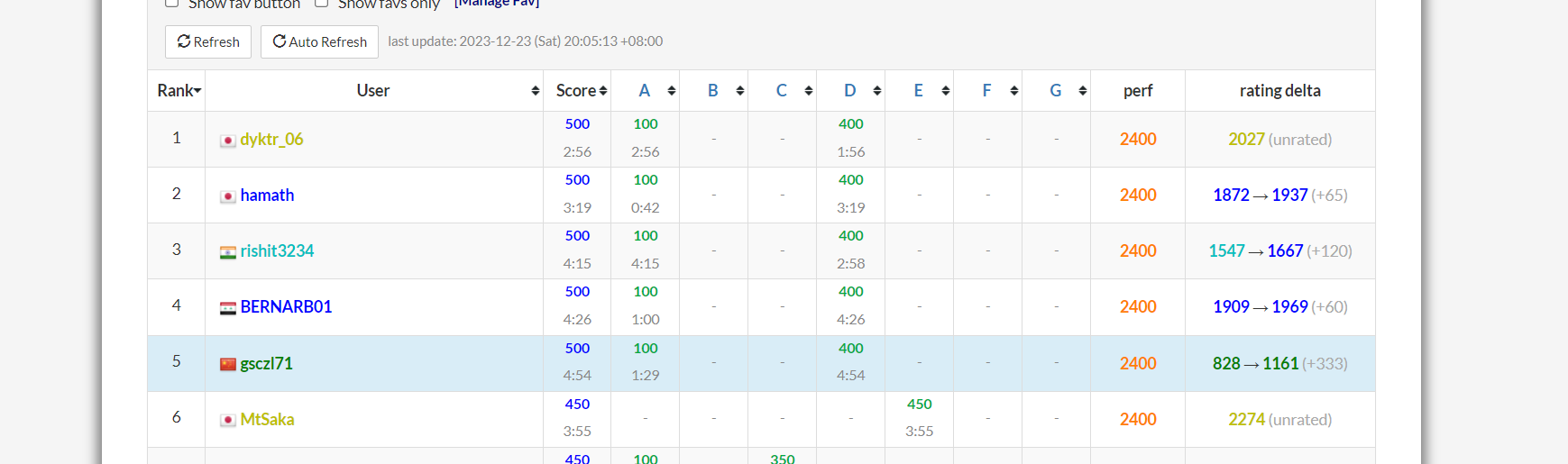
A
比较弱智
link
B
最难了,我切了很久啊。换了很多种方法。
link。
核心代码:
int a,m,l,r;
cin >> a >> m >> l >> r;
l-=a,r-=a;
if(l>0) cout<<(r/m-l/m+(l%m==0));
else if(r>0) cout<<(r/m+(-l)/m+1);
else cout<<((-l)/m-(-r)/m+((-r)%m==0));
我们可以通过取模的性质。然后知道一个数模 \(m\) 等于 \(a\) 模 \(m\) 的地方有树。首先我们不妨先将 \(a\) 的位置看成 \(0\) 点。我们可以抽象的理解,利用 \(m\) 分了很多个区间,每一个区间都是长度为 \(m\),然后算出 \(l\) 和 \(r\) 分别属于什么区间,然后两个区间编号一减,其实就是他们中间树的个数。如果左端点在树上,还要再加一。
因为涉及到正负性的关系。所以需要稍微分类讨论一下,然后注意细节即可。
罚时3次。
C
首先,我们可以分两种情况讨论,如果是偶数,那么排完序之后 \(a_i - a_{i-1}\) 算出来即可。
奇数我们可以预处理一个前缀和和一个后缀和。然后枚举中间哪一个是不用取的,然后使用 \(O(n)\) 时间复杂度解决。
注意一下细节,首先你遍历的时候一定是 \(+2\) 这样跳的,如果是 \(+1\) 的跳就会错,我被卡了很久。
link。
D
最简单的一道。只需要前缀和一遍,二分即可。
link
2023.12.27 ABC267 VP (OI赛制)
A
很简单的题目。
B
题目比较抽象,理解了一下,实际很简单,因为时间复杂度随随便便搞都没有问题
C
没有考虑负数,ans初始0喜提保龄
D
考场想复杂了,认为前面的转移需要用到树状数组维护最大值,实际上,写出来后样例1AC1WA,后面想到其实一个数组实时滚动即可。于是一个dp一个a互相转移就行了,但是最后还是保龄了。老师一讲就恍然大悟,这不是背包板子吗。行了,就过了。
E
顺手一丢题解放上来:
首先,出题人非常滴友善,提供了最大值最小字样,学过 OI 的选手一样就看出来了!二分!!
确实的,这一题就是二分。
我们可以直接二分答案,然后根据 \(mid\) 去进行广度优先搜索,遍历到的这个点的所有连接的点权之和必须小于这个 \(mid\),不然就是不可以加入,然后在广搜遍历的时候,如果这个点 \(i\) 合法,还要将这个点 \(i\) 所连向的所有点 \(j\) 减去一个 \(a_i\),使得实时更新每一个点目前周围的点的点权之和。
于是通过一个搜索板子题目,我们愉快的 AC 了。
link。
我也不知道我是为啥的没看出来,明明很典型啊。可能是没他仔细想吧,几乎整个考试过程都一直在被D弱智着。
F
题解通道关了!喷!
赛时的时候想到了树上距离,倍增,可以用LCA来解决。大概就是分情况倍增,我也不知道我是怎么想的,竟然只想到两种可能,就是跳祖先,和跳孙子,然后跳孙子竟然也写了倍增!我太聪明了。。
首先我们肯定尽可能让 \(u\) 有一个可以到达尽可能远的结点,例如他最远的结点是 \(p\) ,那么 \(p\) 开始往下建一棵树,然后在树上找 \(u\) 的 k 级祖先即可。很容易想到可以建立倍增表来搞,但是实际上,根据dfs序的定义,可以知道假设这个点是第 \(x\) 个遍历到的,那么它的k级祖先便是 \(x-k\) 遍历到的点。所以说,可以直接 \(O(1)\) 解决掉祖宗问题。
实际上直接跑三遍dfs
第一次从1开始遍历,找到最远的点,就是树的直径的一端,然后再找最远的点,就是树的直径的另一端。
所以我们在两个直径端点跑dfs的时候顺便就可以看一下这个点的是否被查询了。然后对ans进行记录,一般对于 q 组询问都是在线回答,但是这种离线的处理方式也是非常的巧妙。
G
题目描述
给定一个正整数序列 \(A=(a_1,a_2,\ldots,a_n)\),问有多少个 \(1\sim n\) 的排列 \(P=(p_1,p_2,\ldots,p_n)\) 满足:
- 存在恰好 \(k\) 个整数 \(i(1\leqslant i\leqslant n-1)\) 满足 \(a_{p_i}<a_{p_{i+1}}\)。
思路
有那么一点点抽象,但是还是可以理解的。
我们不妨将问题转化一下:将 \(a\) 数组重排变成 \(b\),然后 \(b\) 上有 \(k+1\) 个连续的不上升序列(递减)。
如图:

这一张图片中黑色点代表着每一个 \(a_i\) 的值,然后蓝色的线段代表着每一对 \(a_{p_i}<a_{p_{i+1}}\),红色的线段则是连续的不上升序列,然后第 \(i\) 个连续的不上升序列的开头和第 \(i-1\) 个连续的不上升序列的结尾可以形成一对(\(a_{p_i}<a_{p_{i+1}}\))。相当于要 \(k+1\) 个连续的不上升序列。
因为 \(a\) 的顺序不重要,不妨先排序。
我们可以理解,每一次加入的 \(a_i\) 有两种情况:
- 第一种 \(a_i\) 加在所有数之前。如图:
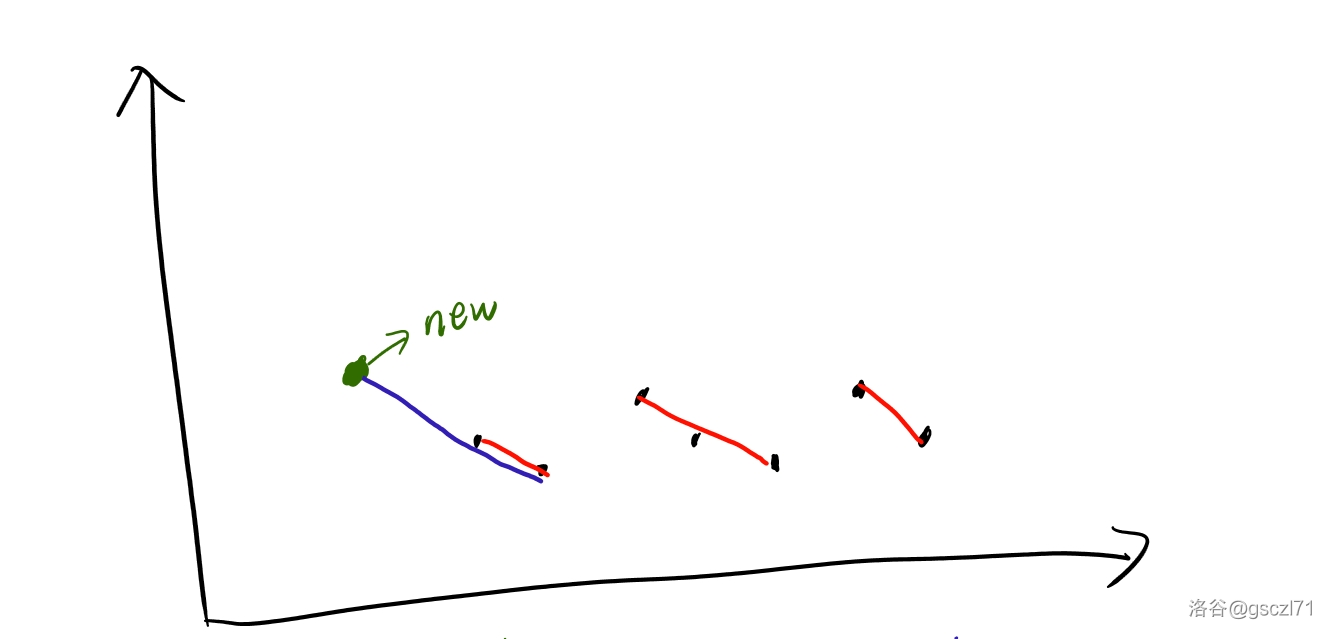
图中绿色点为新加入的点,由于这个点肯定是目前最大(大于等于其他点)。肯定能与目前的第一个点的红色线段连在一起(即蓝色线段),换句话说,就是这种情况连续的不上升序列是不变的。
- 第二种 \(a_i\) 加在中间。如图:

图中蓝色的点加入使得一个红色的线段变成了两个独立的线段,所以说连续的不上升序列加一。
但是,聪明的你会发现:如果有重复怎么办?
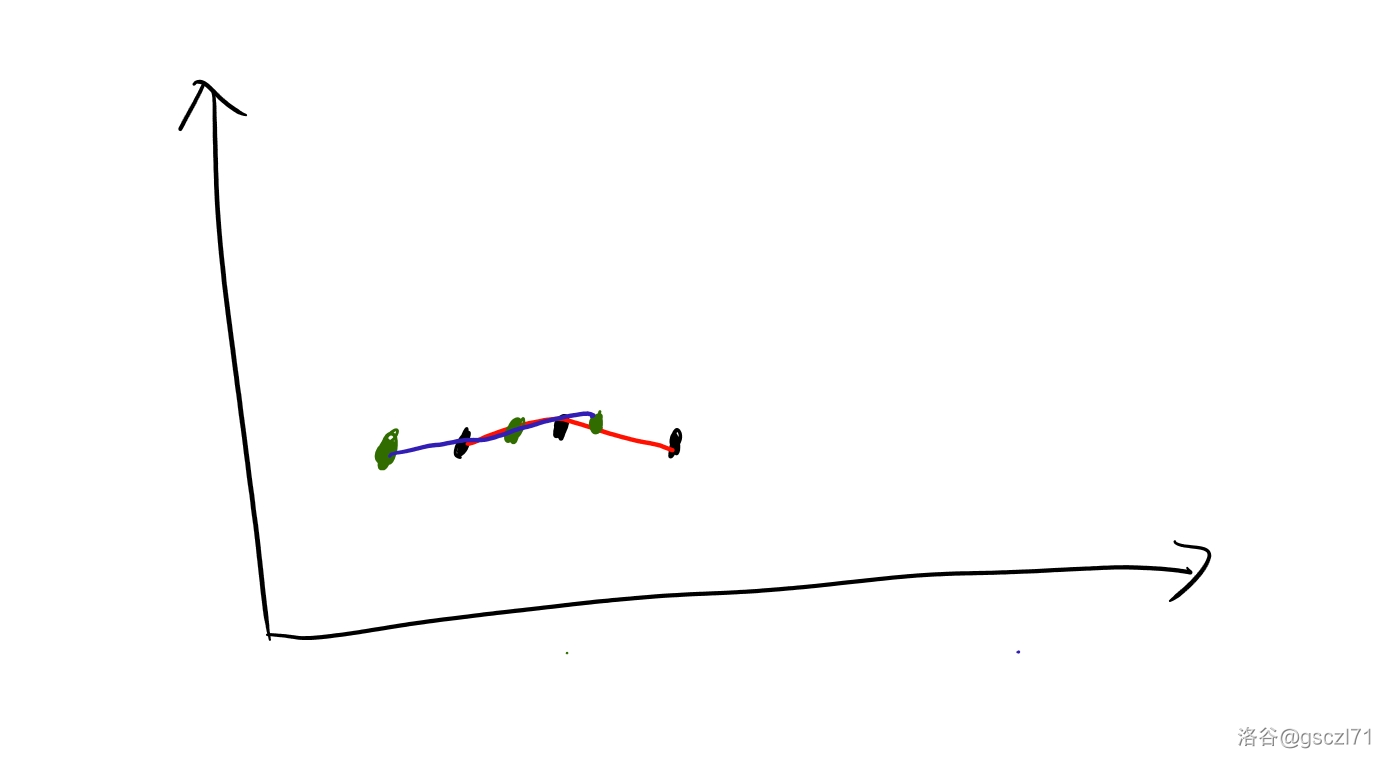
例如,这个是第一种情况,如果有相等的点那么我们可以有多种可能,图中的绿色点都是合法的方案。假设之前已经有 \(vis_x\) 个点等于 \(x\),那么此时必将是可以放在 \(vis_x+1\) 个位置上,\(1\) 是之前的连续不上升序列的个数。所以,我们只需要实时维护 \(vis\) 即可。
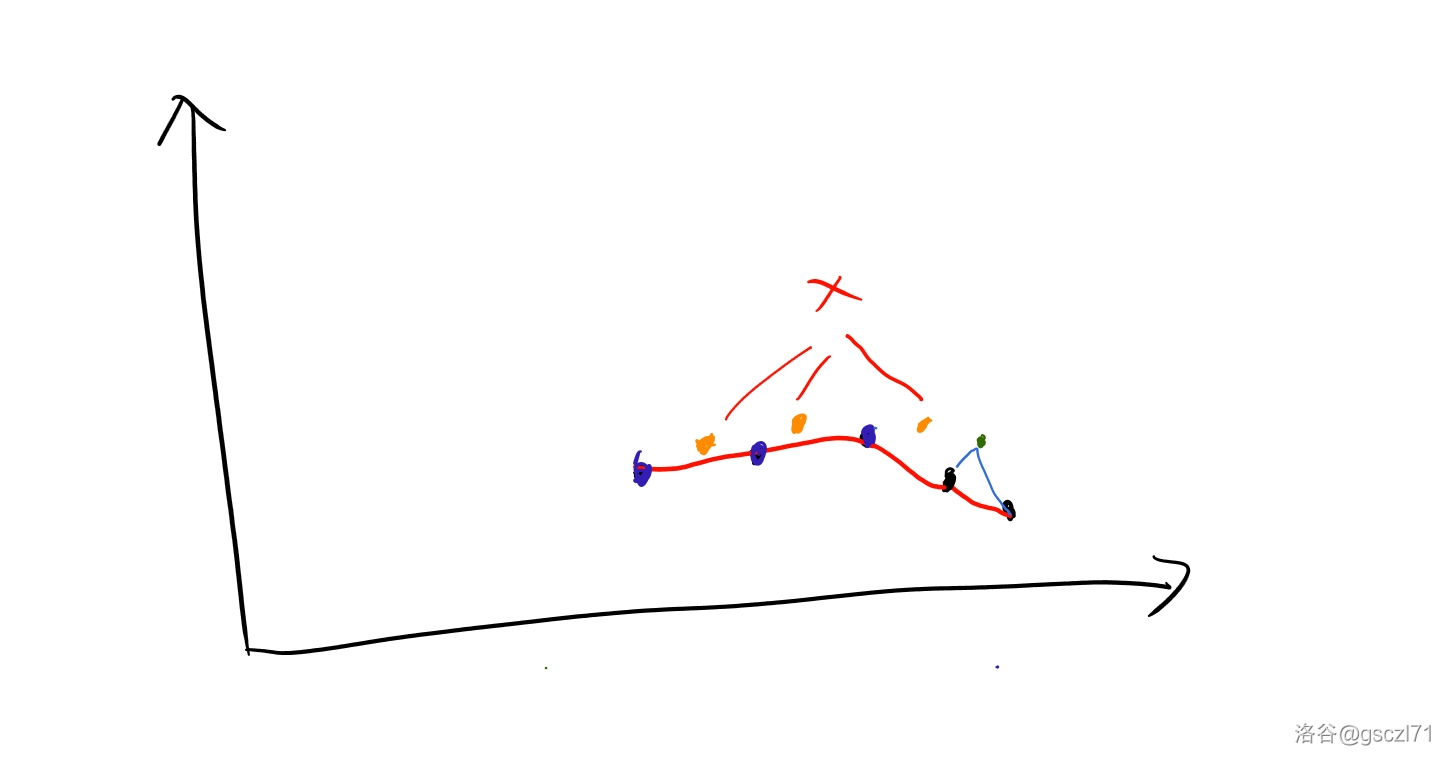
这是第二种情况。从图中可知这个点只能放在绿色位置,不能放在橙色位置,为啥呢,因为它等于了,所以没办法多造一个连续的不上升序列了。那么方案数就是 \(i-j+1-vis_x\),\(i-j+1\) 就是正常的空位的个数,然而 \(vis_x\) 个数挡住了,于是就减掉。
这样我们就可以得到状态转移方程了,使用 DP 进行状态转移,时间复杂度 \(O(nk)\)。通过咯。
link。
标签:AtCoder,遍历,Beginner,Contest,一个,可以,然后,link,dp From: https://www.cnblogs.com/gsczl71/p/17880643.html