你是跑码场的一个程序员,名字叫招财。
利用上班摸鱼的时间编写了一个简易的即时通讯软件,并发布到了网上。过了一段时间,你在软件上突然收到一条私信。
“小哥哥,我很喜欢你写的这个软件,我也是程序媛,希望以后能多多和您交流。”
你望了望四周,没有人表现得异常,于是你确认不是同事在逗自己。
你兴冲冲地给对方回复,一来二去,慢慢熟识了起来。你知道了对方的名字,叫小美。
1、不安全的明文
随着交流的话题越来越深入,你也慢慢变得惶恐。你本来就是随手写着玩儿的软件,消息都是明文发送的,这万一被研究网络的同事给监听了,以后在公司还怎么混?
于是你想到了:加密。
2、对称加密
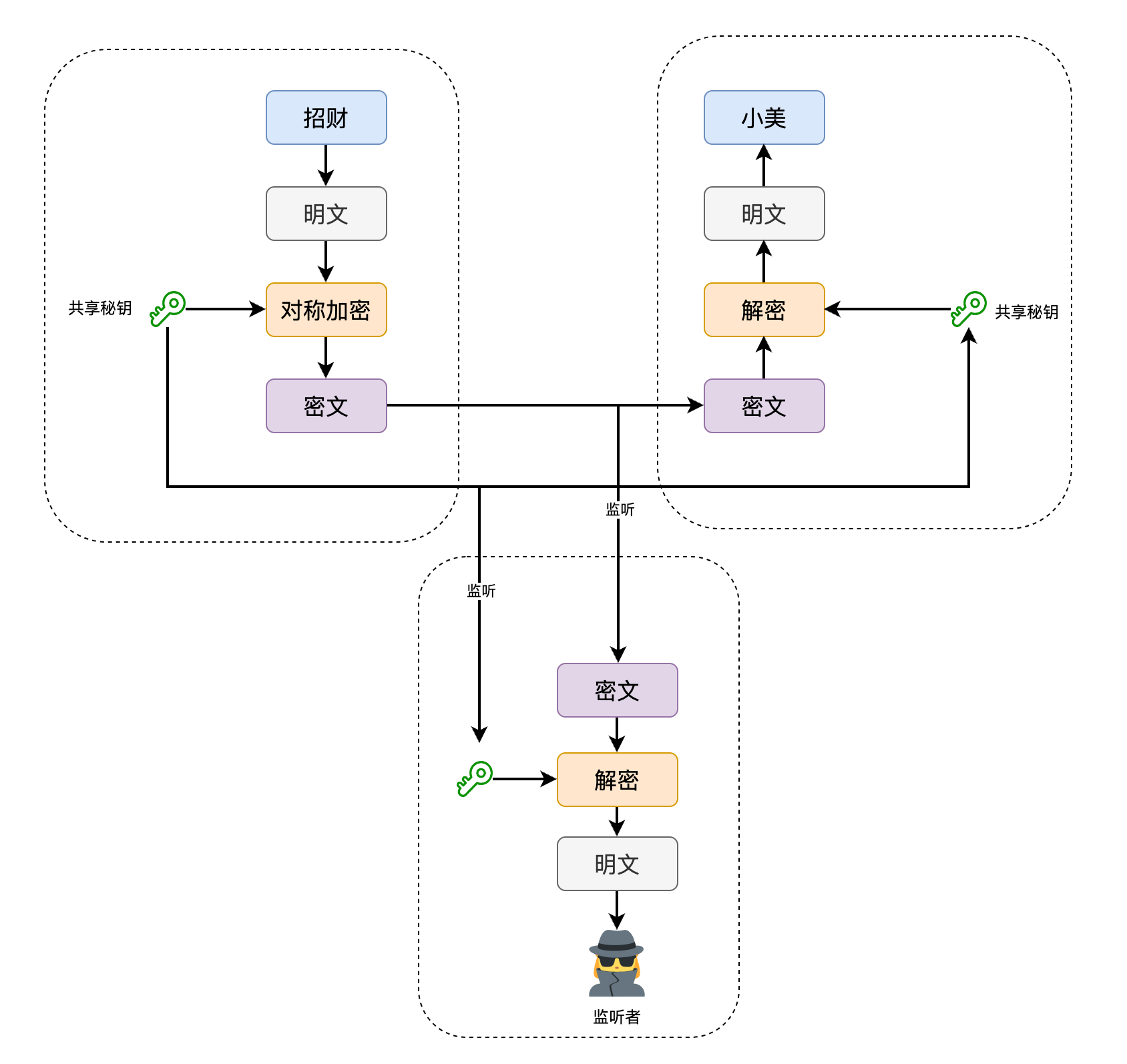
如果双方拥有同样的钥匙,发送消息的一方使用这个钥匙进行加密,接收消息的一方使用同一个钥匙进行解密。这么一来,加密的事情就变得简单了。
为了实现这个功能,你想到了之前学过的异或(XOR)操作,这个操作的规则总结起来就是:相等为0,不等为1。任何数据在计算机中都会最终表示为01的字节流,比如你想发送的消息被最终编码为1001110011001110,然后随机生成一个同样长度的字符串1011011100110011,称为秘钥,两者做一下异或操作:
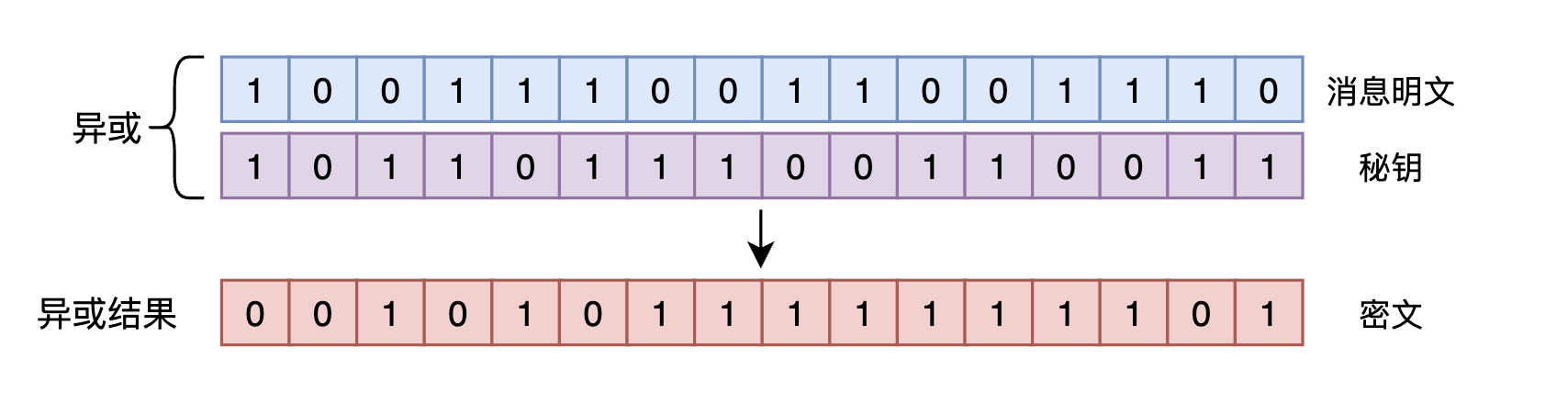
消息明文与秘钥进行异或操作之后就得到了密文,按照异或运算的性质,如果此时将密文再和秘钥做一次异或操作,那么将重新得到消息明文。
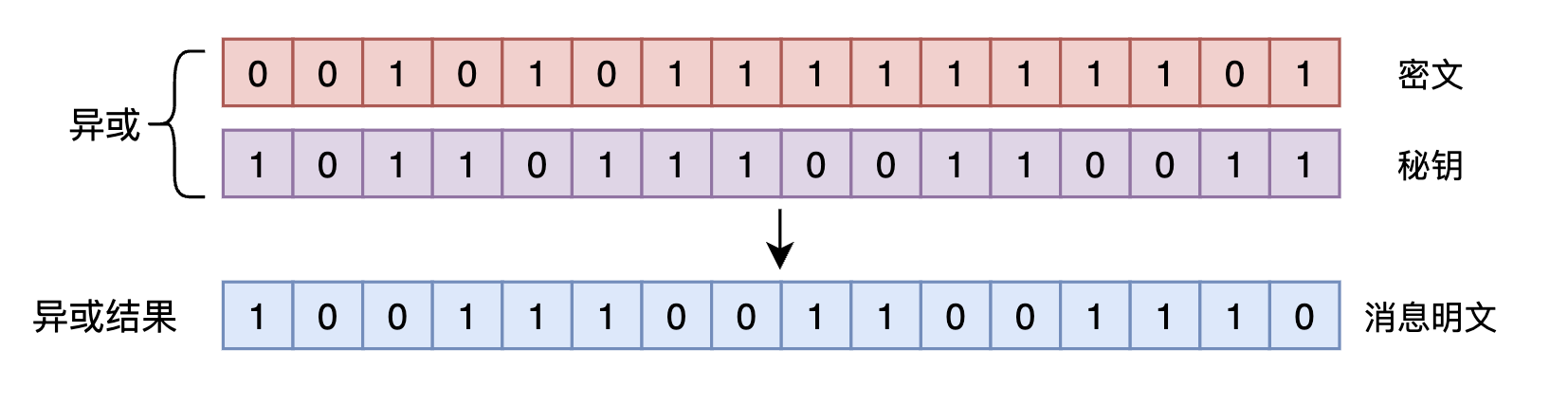
如此一来便实现了双方使用同一个共享秘钥对消息进行加密/解密的操作。
但是目前有个问题,你生成的秘钥长度必须和消息的长度保持一致才能做异或操作,除非你对异或操作进一步封装。你才懒得琢磨这些东西呢,于是上网找思路。
这才知道,你的想法其实就是对称加密。DES、3DES以及AES密码算法都属于对称加密,其中或多或少都利用了异或运算的性质,否则就没有了“对称”的效果。
你选择了目前最流行的AES算法,打算直接使用现成的类库实现加密。你把这个想法告诉了小美,迫不及待地想让她知道你们的对话已经实现了机密性。
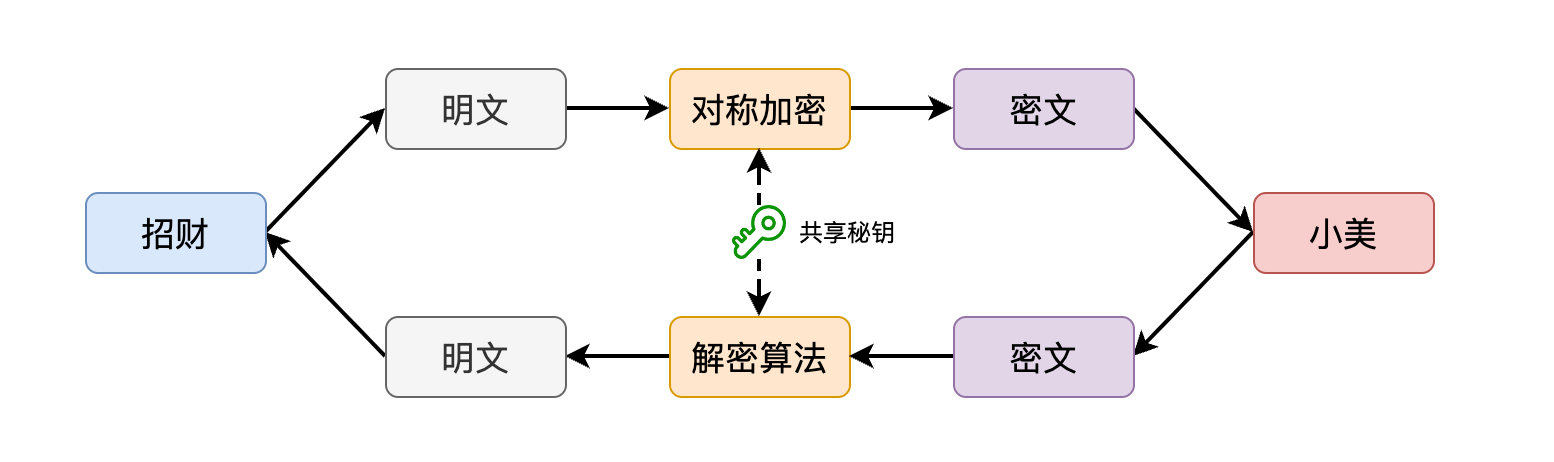
谁知,小美一针见血地指出了问题,“秘钥如何安全地在我们之间进行共享呢?”
是啊,监听者也是可以获取到秘钥的。这样就很矛盾,如果有一个办法能将秘钥安全地共享出去,那么岂不是也可以用同样的方法来安全地发送明文咯?
对称密码的秘钥必须发送,而又不能明文发送,这就是对称秘钥的配送问题。
3、非对称加密
于是你又开始寻找其他方法,终于发现了一种叫做公钥密码的算法。
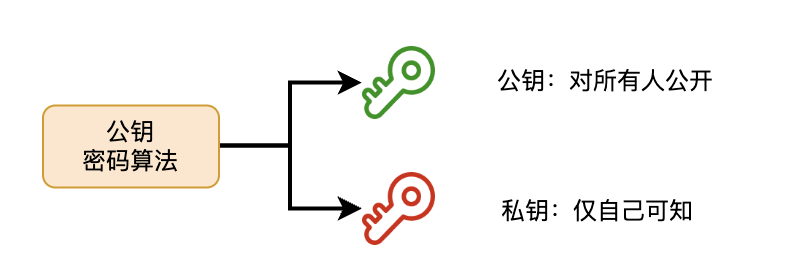
这种算法可以生成一组密钥对,分别叫做公钥和私钥。正如其名字暗示的那样,公钥是可以公开的,地球人都可以知道,而私钥必须自己保存好,打死也不能让别人知道的。
由公钥进行加密的密文,必须使用与该公钥配对的私钥才能够解密。反过来,使用私钥进行加密的密文,拥有公钥的人都可以进行解密。这个特点非常重要。
于是你生成了一组密钥对,并将公钥发给了小美,自己保存好私钥。你让小美给你发送消息之前先用你的公钥对消息进行加密,这样一来,小美的加密消息只有你的私钥才能够解密。
于是便实现了小美对你发送消息的机密性。
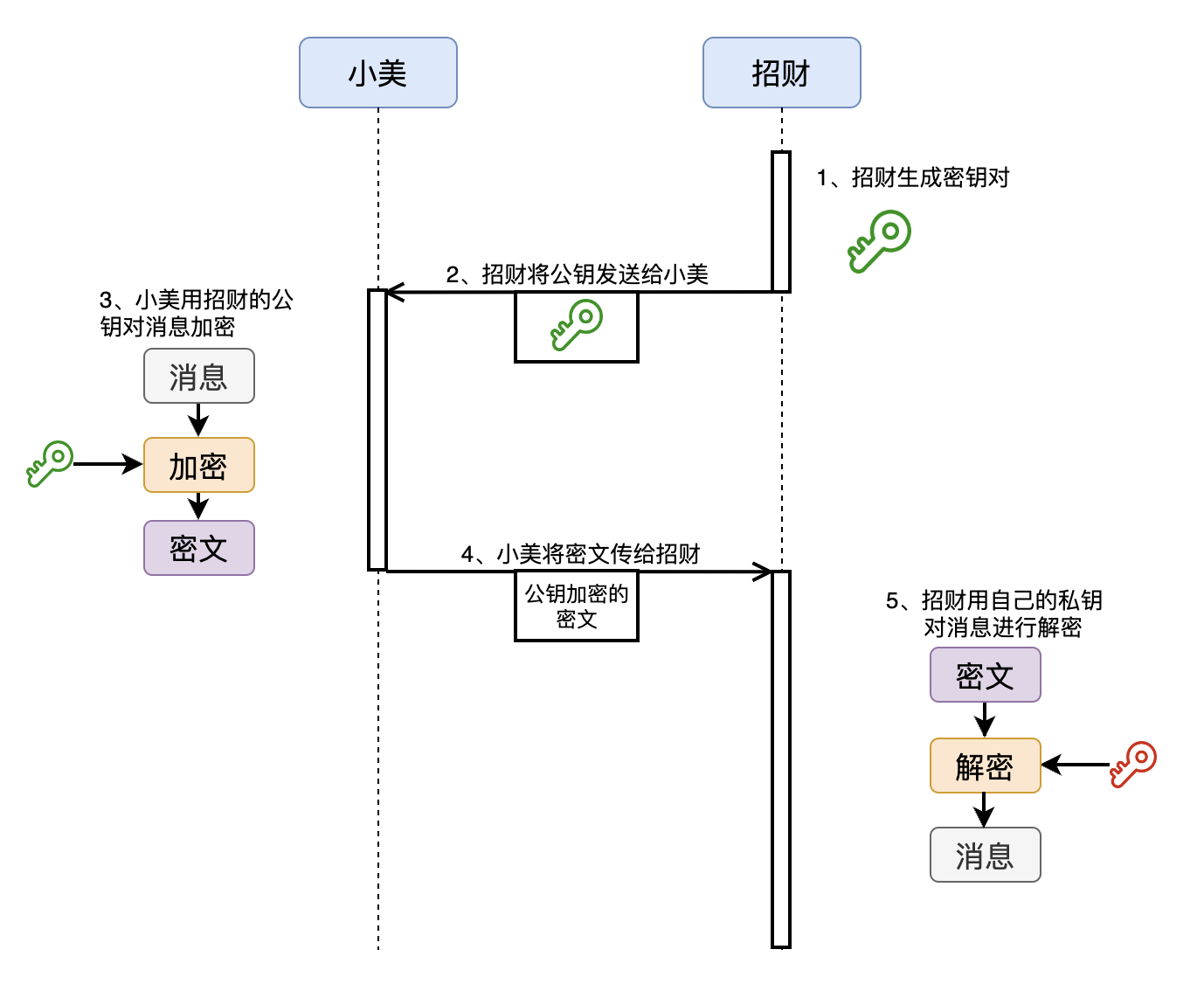
反过来,如果要实现你对小美发送消息的机密性,就需要小美生成一组密钥对,你获得小美的公钥,然后发送消息之前首先用小美的公钥对消息进行加密,将密文发送给小美之后,小美再用她的私钥进行解密。
如果通信过程中的公钥和密文被监听者获取到也没关系,因为你们两人的私钥都没有出现在通信过程中,监听者即使有了密文也没法解密。
这样一来,你通过了公钥加密解决了消息的机密性和秘钥的配送问题(因为压根不需要配送对称加密的秘钥了)。
公钥密码还有一个名字,叫做非对称加密。这个名字是相对对称加密而言的。
对称加密是使用同一个秘钥进行相反的运算,因此对称密码中的加密和解密就像照镜子一样,是相互对称的。非对称加密中,加密和解密使用的是不同的密钥,并非相互对称,因此称为非对称加密。
注:大名鼎鼎的
RSA算法和ECC(椭圆密码曲线)算法都是公钥密码算法的具体实现
4、混合加密算法
公钥加密的改进让你感到非常踏实,现在满脑子里装的都是跟小美聊天。可是你逐渐发现,小美的回复变得比之前慢了一些。
和小美沟通一番之后发现,她对你的回复也有同样的感觉。
聪明的你最终发现了原因,公钥加密的算法效率太低下了!在采用具备同等机密性的密钥长度的情况下,公钥加密的速度只有对称加密的几百分之一。
知道了问题,解决方案也是很明显了,把对称加密和公钥加密结合起来使用,也就是混合加密。
既然是混合加密,自然既要传送消息,又要传送对称加密的秘钥。你先用加密效率很高的对称加密算法对消息进行加密,这样就实现了消息的机密性。接下来只要保证对称加密秘钥传输的机密性就可以了。
这时候又要用到公钥加密了。你将对称加密的秘钥当做消息,利用上文公钥加密的步骤,先使用小美的公钥对对称加密的秘钥进行加密,小美收到之后再用自己的私钥进行解密,就能安全在你俩之间传递对称加密的秘钥了。
你也不用担心效率问题,毕竟对称加密的秘钥通常比消息短得多,况且秘钥的传递只需要一次就可以了,因此加密的时间代价可以忽略。
画一下使用混合加密算法时,你发送消息进行加密的流程图。
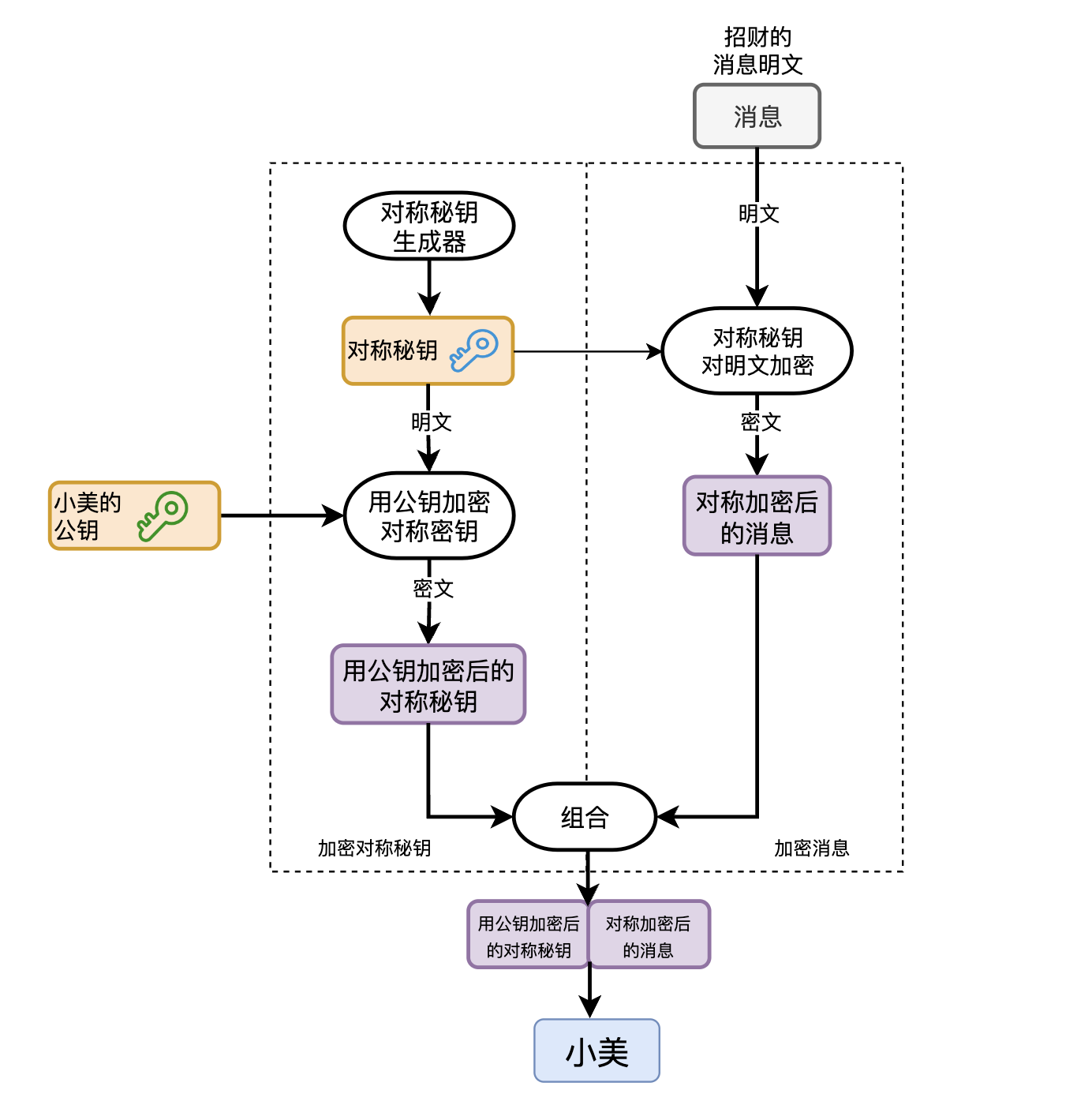
懂了加密,解密也就很简单了,为了让小美看得明白,你还是给她画了个解密流程图。
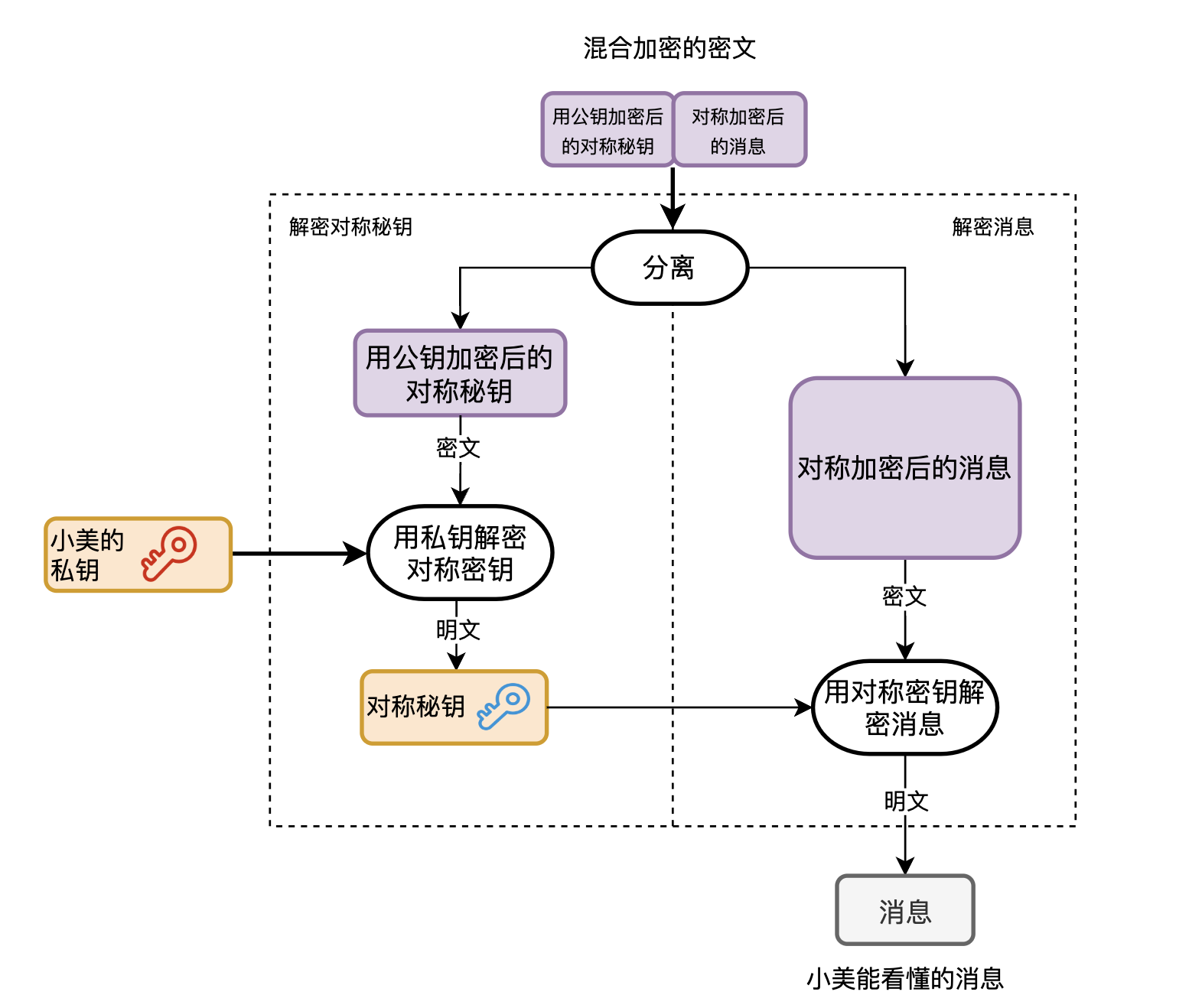
到此为止,你解决了公钥加密速度慢的问题,并通过公钥加密解决了对称秘钥的密钥配送问题。
5、谁改了我的消息
你和小美聊得愈发火热。但是你最近总是时不时收到小美发过来的莫名其妙的文字。你开始不以为意,但是这种文字的发送频率越来越高,实在搞得你头大。
你赶紧问了问小美,在确定不是她故意发这种文字之后,你明白了。
你俩被人盯上了。。。
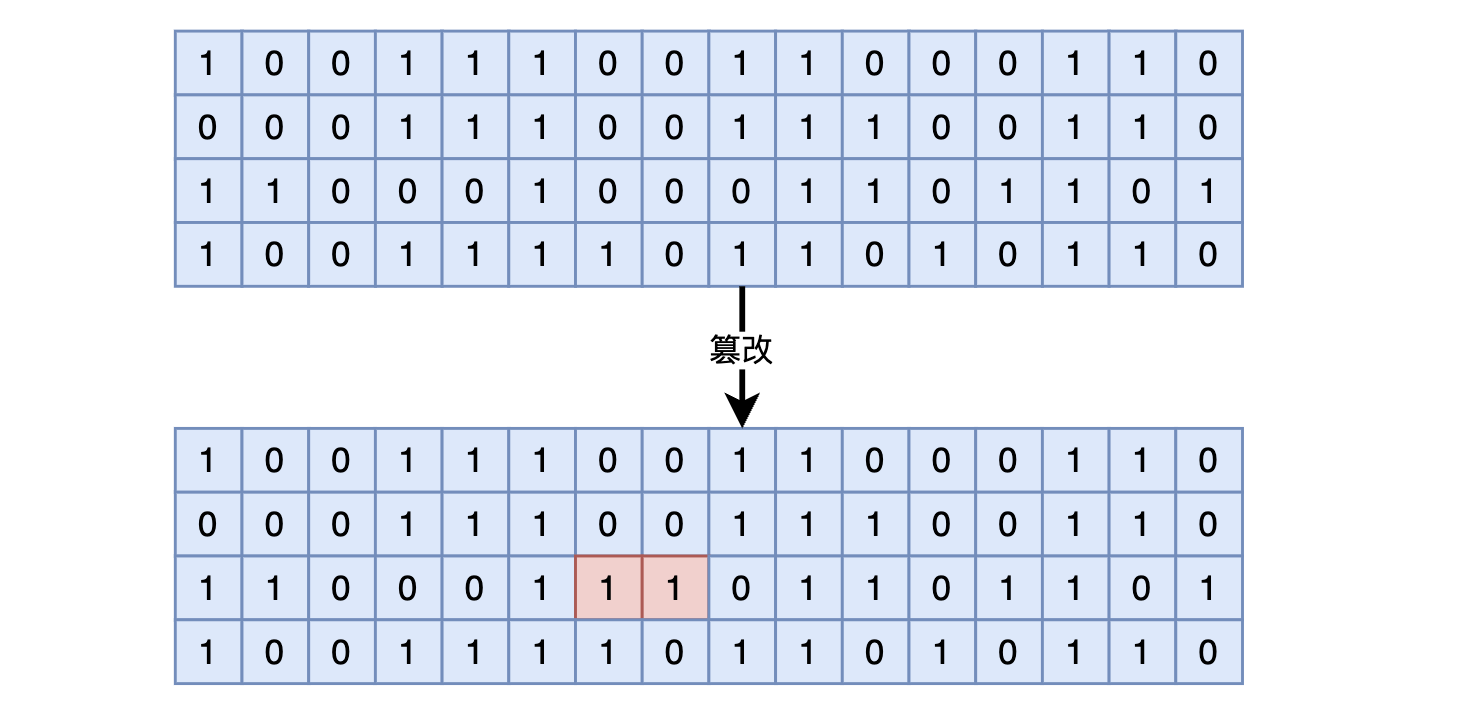
你分析了一下小美实际传给你的加密消息与你实际收到的加密消息,发现编码之后的数据有两位比特被改变了。改变虽然不大,但是对消息的可读性会造成相当大的影响。
你遇到中间人攻击了。
这种情况下,中间人不需要知道你俩聊得究竟是什么,只需要截取你们的消息,然后进行随意篡改,就能扰乱你俩之间的正常交流。
你不禁感叹:怎么传递个消息就这么难呢!
好在这个问题不难解决,你马上就想到了单向散列算法。
单向散列算法可以对任意长度的消息生成一个固定长度的一串数据(散列值),这串数据的长度远小于输入的消息长度,因此又被称为消息摘要,单向散列算法也因此被称为消息摘要算法。
摘要算法可以实现消息的完整性检查。
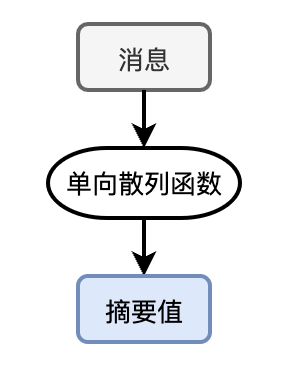
消息摘要算法的一个巨大好处是对消息的变化极为敏感,哪怕对消息仅修改了1个比特,生成的消息摘要也会有翻天覆地的变化。而且,即使中间人截获了摘要消息,他想自己伪造一个经过散列能够生成同样摘要的消息几乎是一件不可能的事情。
注:经常听到的
MD5、SHA-1、SHA2、SHA3算法都是消息摘要算法的具体实现
于是你在消息发送和解析过程中又添加了对消息摘要算法的支持。发送数据之前,先对混合算法加密之后的密文计算摘要值,然后将摘要值附在密文的最后,一起传输给小美。
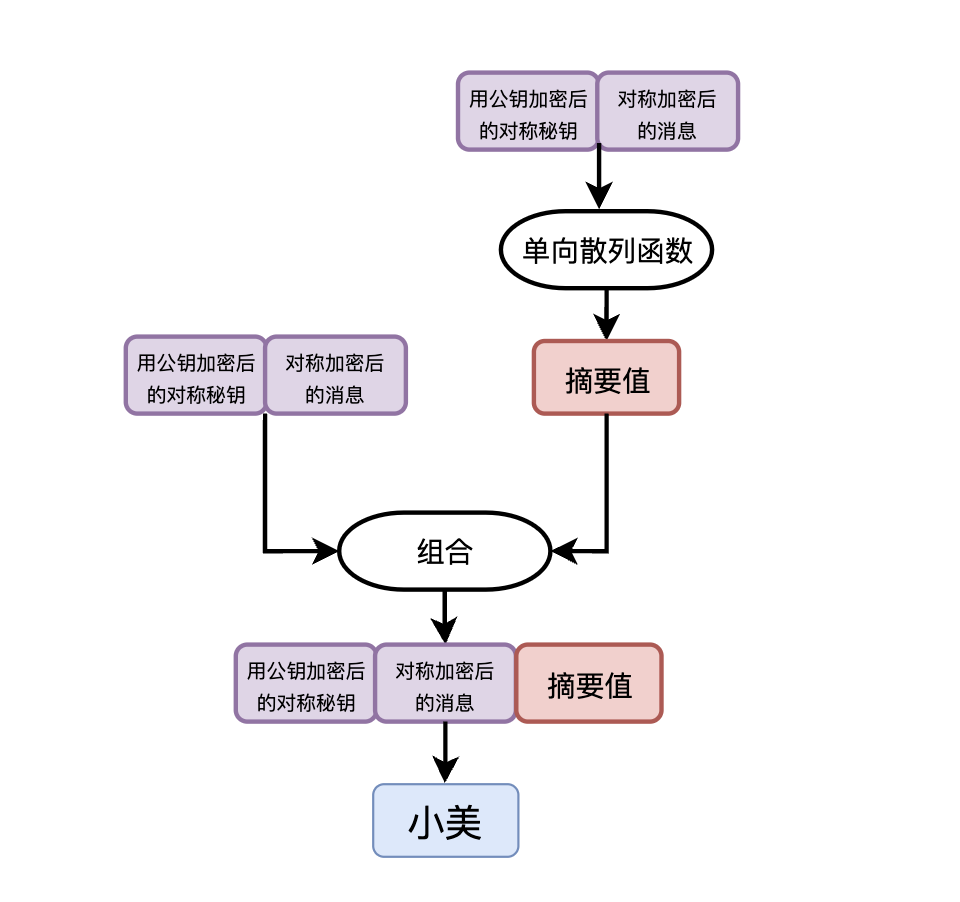
小美收到数据后,根据信息摘要的固定长度,首先分离摘要值和密文,然后使用相同的摘要算法计算出密文的摘要,与接收到的摘要进行对比,一致则表示信息没有被篡改,否则就说明被动了手脚,直接丢弃。
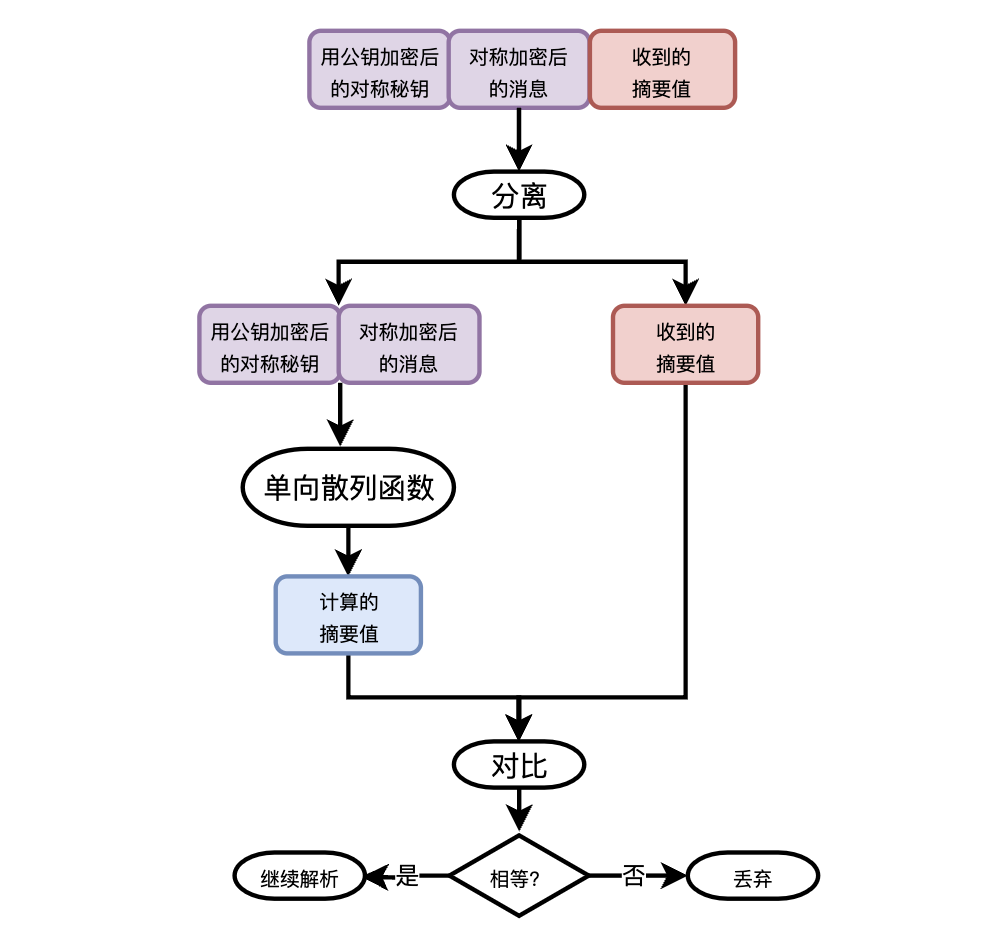
你认为事情到这终于结束了。但是软件更新之后,你发现还是会时不时收到莫名其妙的消息。
6、是谁在冒充
你思来想去,问题到底出在了哪里?
“会不会是我们的消息整个都被篡改了啊。”小美说道。“如果中间人监听到了整个消息,分离出了混合加密的密文和摘要值,然后篡改混合加密的密文,再重新对篡改之后的密文计算出一个新的摘要,附在篡改的密文之后再发送,我们根本无法识别出篡改。”
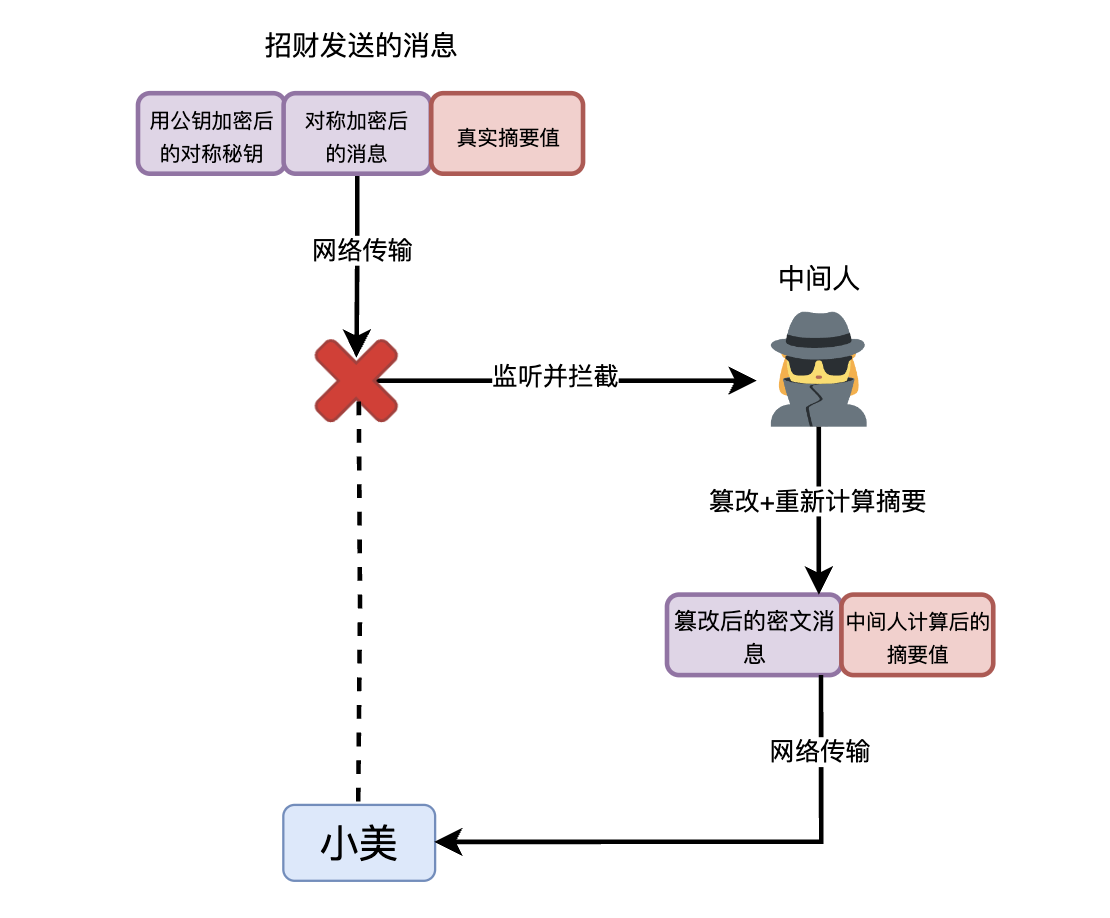
是啊,如果真的是这样,摘要值检查的实际上就是中间人发送的消息的完整性,这个检查就失去了意义。
现在中间人已经彻底挟持了通信线路,只要中间人想,他就能篡改你们之间的所有数据。换句话说,你现在根本不知道和你进行通信的是小美还是中间人。
这就是单向散列函数的缺陷,能够辨别出“篡改”,但是无法分辨出“伪装”。
你现在需要实现消息的认证功能。也就是说,你对小美发送的消息,需要向小美证明消息确实是你发的,并且没有被篡改。同样,小美对你发送的消息,也需要向你证明,消息确实是小美发的,并且没有被篡改。
7、确认对方身份
于是你跟小美商量,需要约定一个只有你们两人才知道的「信息」,并且通过接收到的消息可以判定,只有拥有这个共同信息的彼此才能发出这条消息。
小美立刻想到,“我们一直在使用的对称加密的秘钥不就是这个「共同信息」嘛!如果我发的消息你能解密出来,不就证明我就是我了吗?”
“你这么想从一定程度上是对的,但是有个前提条件,就是你发的消息一定是有意义的。如果你本身就是想给我发送一堆乱七八糟的文字,我无法确定这是你的本意,还是说消息已经被中间人篡改了。”
你俩陷入了短暂的沉默。
你思考了一下,摘要值目前无法发挥认证的作用是因为只要中间人获取到了密文,就能随便生成摘要值。那如果给摘要值的生成提高门槛,只有拥有「共同信息」的彼此才能够生成正确的摘要值,这样的话不就能认证了嘛。
这个摘要值就叫做消息认证码。
网上搜索了一番,还真有这种方法,叫HMAC(Hash Message Authentication Code,哈希消息认证码),是用单向散列函数来构造消息认证码的一种方法。
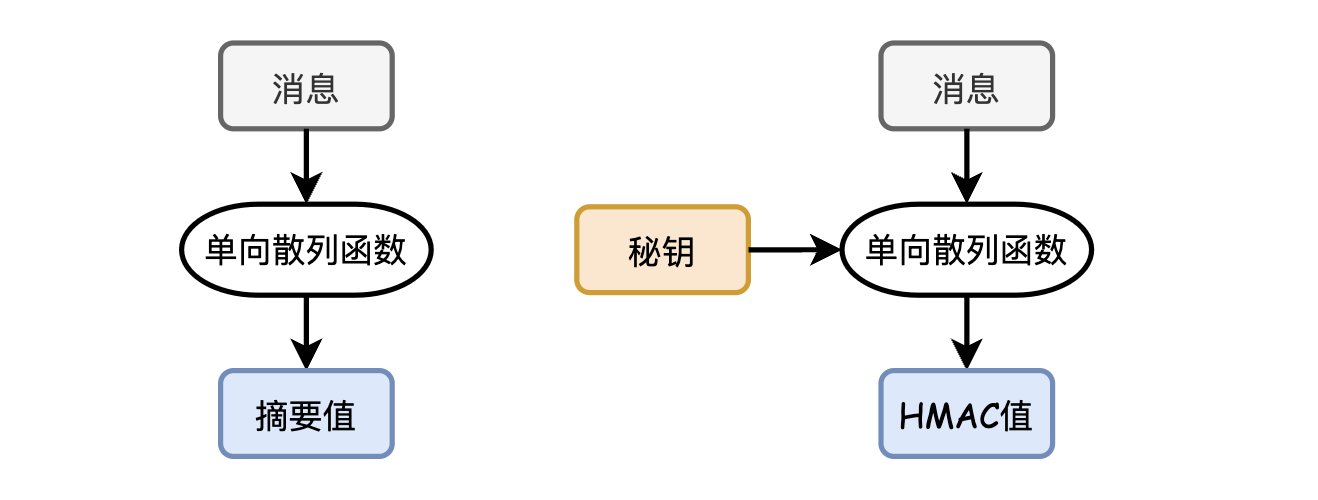
摘要值和HAMC值的最主要的区别就是后者在进行单向散列的时候,需要用到一个秘钥。因此这个可以简单理解为,消息认证码是一种与秘钥相关联的单向散列函数。
有了这个技术,再来看一下你给小美发送消息的过程。
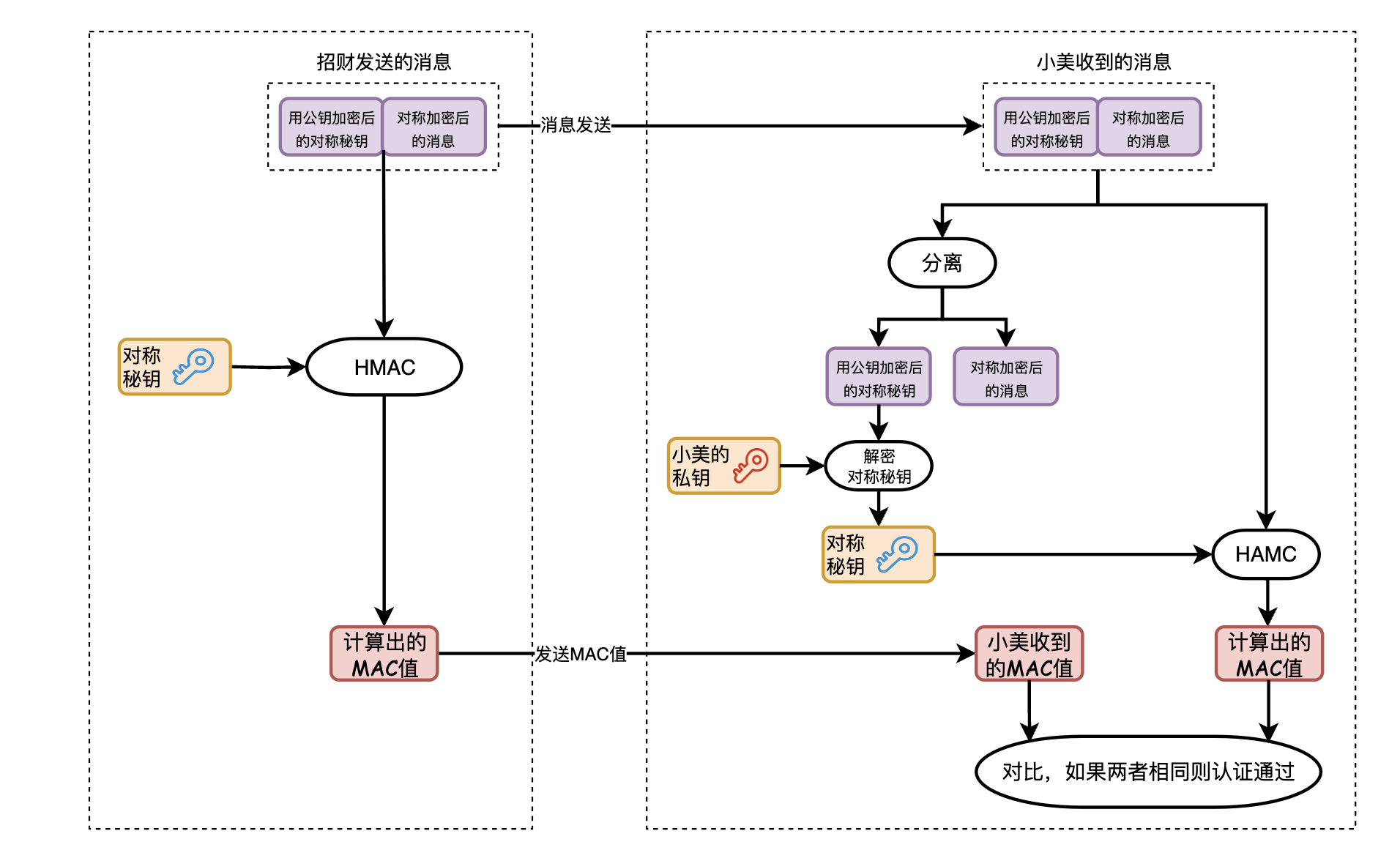
本来应该为HMAC单独生成一个随机秘钥,但是又会涉及到秘钥配送的问题。由于我们之前已经使用公钥解决了秘钥配送问题了,为了方便,就直接使用对称秘钥作为HMAC的秘钥了。
和原来不同的是,用计算出的MAC代替了原来的摘要值,小美接收到密文和摘要值之后。利用自己的私钥解密获得对称加密的秘钥,再利用这个秘钥对收到的密文计算MAC值,如果两个MAC一致,那么小美就可以确定这个消息是你发送的,没有经过中间人篡改。
如此一来,使用MAC值就实现了消息的完整性校验和身份认证的功能。
8、对方死不认账了
突然有一天,小美对你发来了一条消息。
“PHP是世界上最好的语言~”
你当场炸裂啊~说这话妥妥引战嘛,你刚要和小美理论一下,小美紧接着来了句:“我跟你玩个游戏啊。”然后又发送了一个调皮的表情。“你如何证明我对你说了这句话呢?”
“这还需要啥证明啊,我用咱俩共享的秘钥,生成了MAC值,然后和你发给我的MAC对比,是一致的。如果你的私钥没有泄露,我就敢绝对保证,这条消息就是你发的!”
“没错,在咱俩之间,是绝对能保证身份的认证的。但是我的问题是,你如何向其他人证明这个消息是我发送的呢?你想啊,你和我有相同的秘钥,也就是说,理论上这条消息你也能生成。我要是死不认账,你怎么办?当然咯,截图可不算哈~”
小美说得没错,按照现在的加密设计,的确没法向第三方证明她说过的话。
现在你俩之间能相互认证是由于拥有同一个秘钥,你确定不是自己发的,那必然就是对方发的。如果想向第三方证明消息是小美发的,那就必须使用小美独有的信息对消息做一下处理。
就好比古代的虎符,如果小美持有其中一半,并且保证私有,这样不管另一半在谁的手里,只要两部分能够合二为一,就能确认对方就是小美。

这不就是公钥和私钥嘛!
小美用自己的私钥对消息计算出一个「签名」,任何持有小美公钥的人都没办法用公钥复刻这个签名,但是可以对小美发送的签名用公钥进行解密,解开的内容如果恰好就是消息本身,那说明收到的消息一定属于小美!毕竟私钥是独一无二的,这下子小美就再也没办法否认了!
但是有个小问题,公钥加密的效率实在是太低了,如果对整个消息使用私钥进行加密,耗时太久。能不能找个比较短的数据来代替消息本身呢?
老朋友——单向散列函数,又该出马了。只要先用单向散列函数求出消息的散列值,然后使用私钥对散列值进行签名就可以了。散列值可比消息本身短得多,因此对其进行签名的时间代价就小得多了。
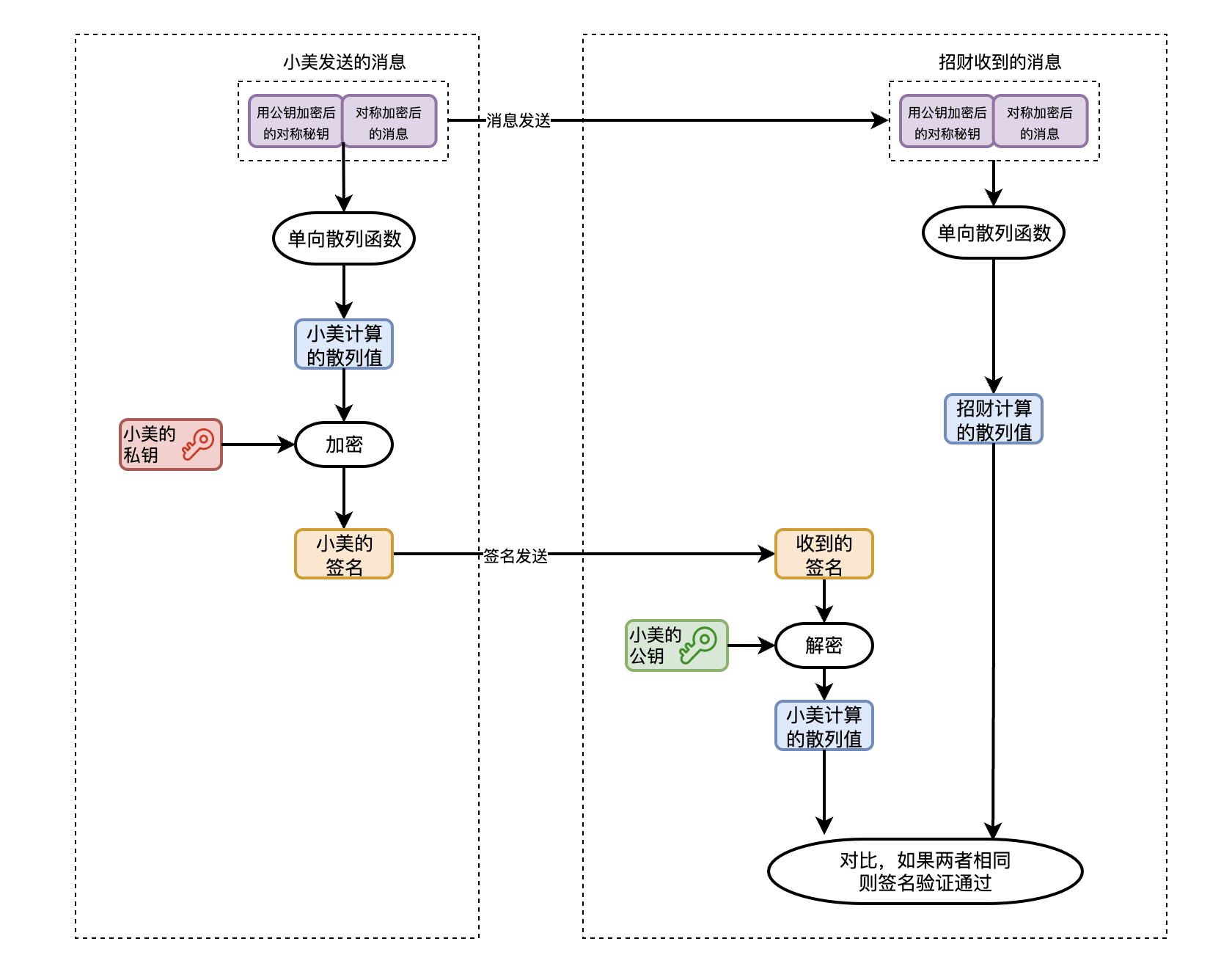
如果中间人篡改了小美发送的消息,那么你计算出来的散列值就会发生变化,导致签名验证失败,签名保证了消息的完整性和对方身份的认证。不仅如此,签名还能防止小美否认之前发的消息。
从图中可以看出,签名已经彻底替换掉了之前使用的消息验证码。
到此为止,你已经实现了消息的机密性、完整性、身份认证以及不可否认性。
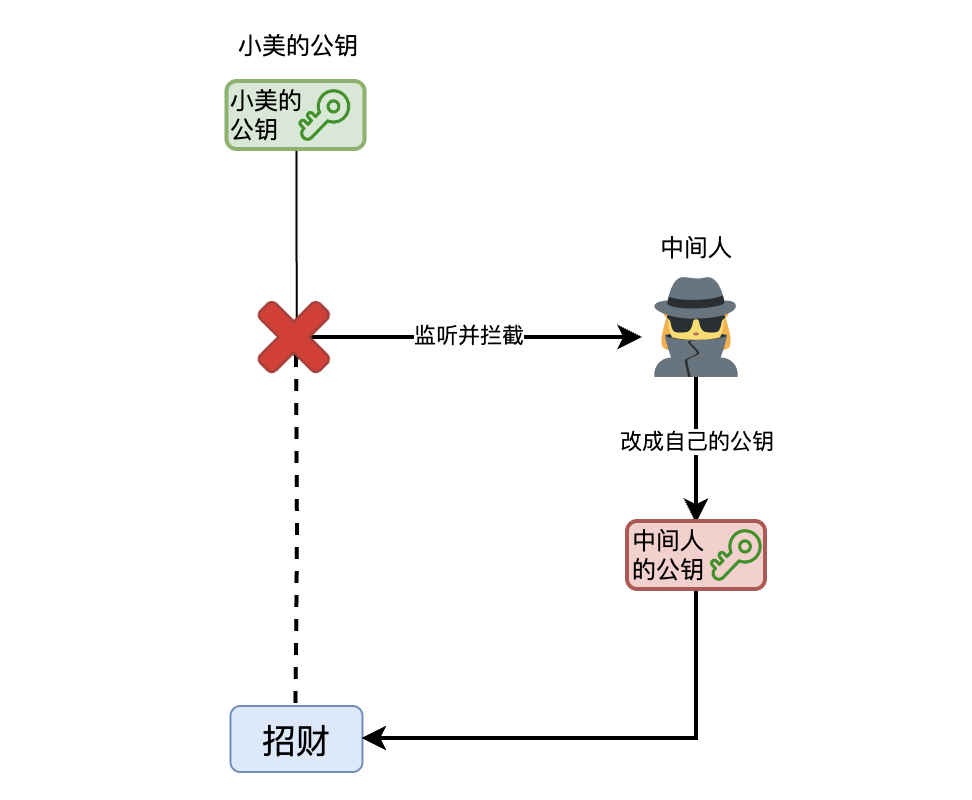
居然不知不觉已经走了这么多路,你不禁问自己,到签名这一步已经完美了吗?签名的验证依赖于消息发送者公开的公钥,那如果从一开始,这个公钥就被中间人劫持,换成了中间人自己的公钥了呢?我们又该如何确保收到的公钥没有被篡改呢?
9、CA机构与证书
你发现自己陷入了一个怪圈。数字签名是用来进行身份认证、防止篡改以及防止否认的,数字签名依赖公钥的传递,公钥的传递又需要进行身份认证以及防止篡改。。。
你把现在的设计告诉了小美,想看看她还有没有其他的主意。
“我觉得你现在设计地已经够好了,接下来已经不是单纯的软件设计能力能够解决的事情了,已经上升到社会学层次的高度了。”
“这是什么意思?”
小美解释道:“就是说,我们应该成立类似于公证处这样的专业机构,来认证公钥的合法性,叫做CA。认证机构也要生成自己的一组密钥对,分成公钥和私钥,私钥自己保管,公钥任何人都可知。”
“那这怎么进行认证呢?”
“还是用你数字签名的思路,比如我在分发我的公钥让你知道之前,我先把公钥发给认证机构,然后认证机构用自己的私钥对我的公钥添加数字签名,最后颁发一个包含我的公钥和认证机构数字签名的证书。这个证书就证明我的公钥是合法的。”小美补充道,然后画了个图。
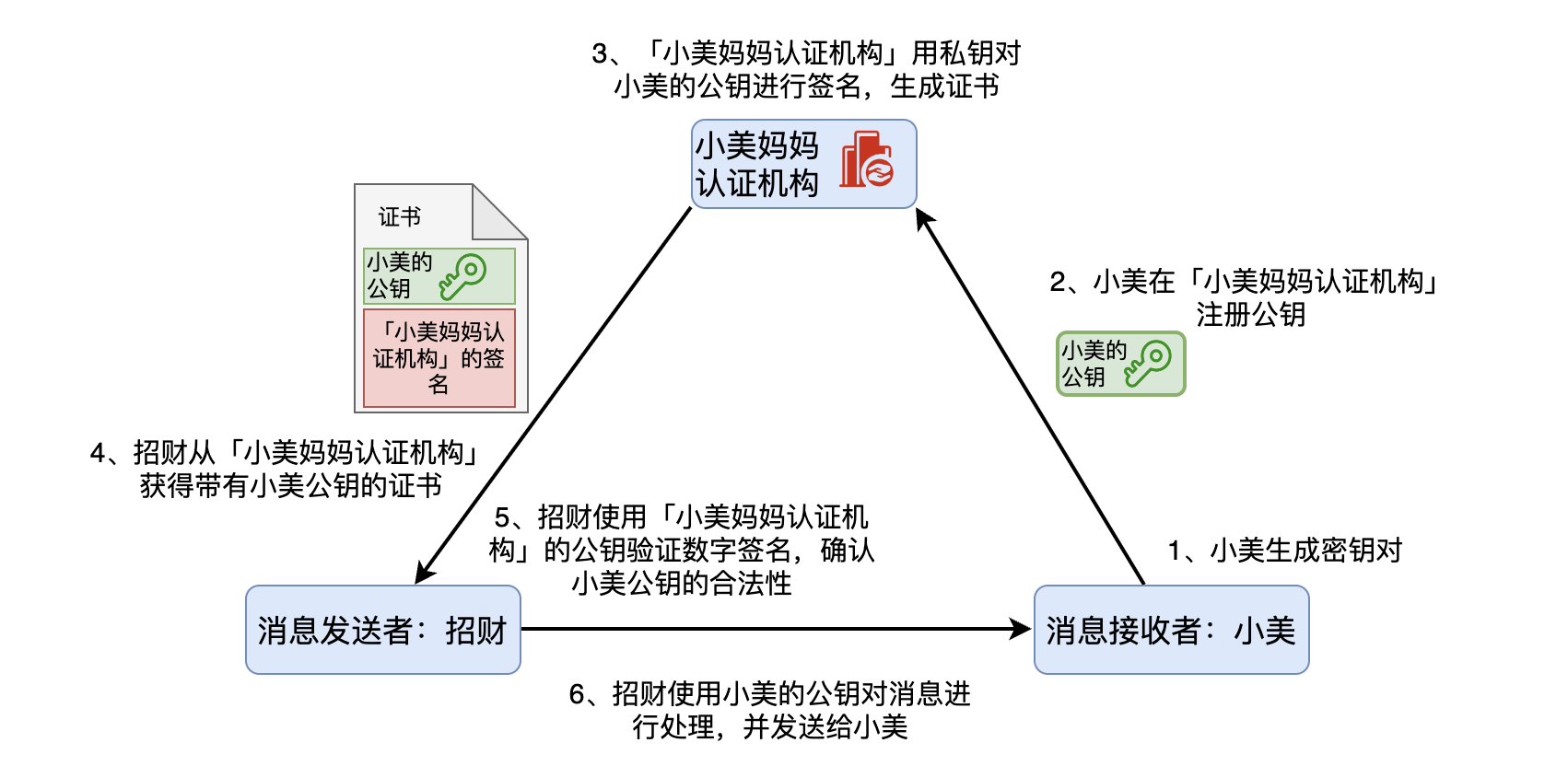
你一眼就看出了这个逻辑的漏洞,这个方案没有从根本上解决问题,只是把问题转移了而已。因为小美妈妈这个认证机构需要对小美的公钥施加数字签名,你势必需要用到小美妈妈这个认证机构的公钥。
“我现在不信任你的公钥,也对你妈妈这个认证机构的公钥有所怀疑,那认证机构对颁发的证书就没有任何意义!依旧是个死循环!“你对小美提出了自己的疑问。
”那取决于你怎么理解『信任』这个词儿了,如果你除了自己谁也不信,那对你来说永远不会有安全的通信,这个逻辑链条就是个死循环。实际上,『信任』这个词儿是比较出来的,在多个供选择的信任对象中只要有一个你最信任的就可以了“。
小美继续说:”我举个例子。你觉得银行愿意把钱借给你是因为信任你这个人本身吗?当然不是,银行相信的是你背后抵押的房子等所有值钱的东西。回到这个例子里,如果我妈妈的认证机构经过层层关系,最终找到了你妈妈的认证机构,你看看这个逻辑是不是就解释的通了。“
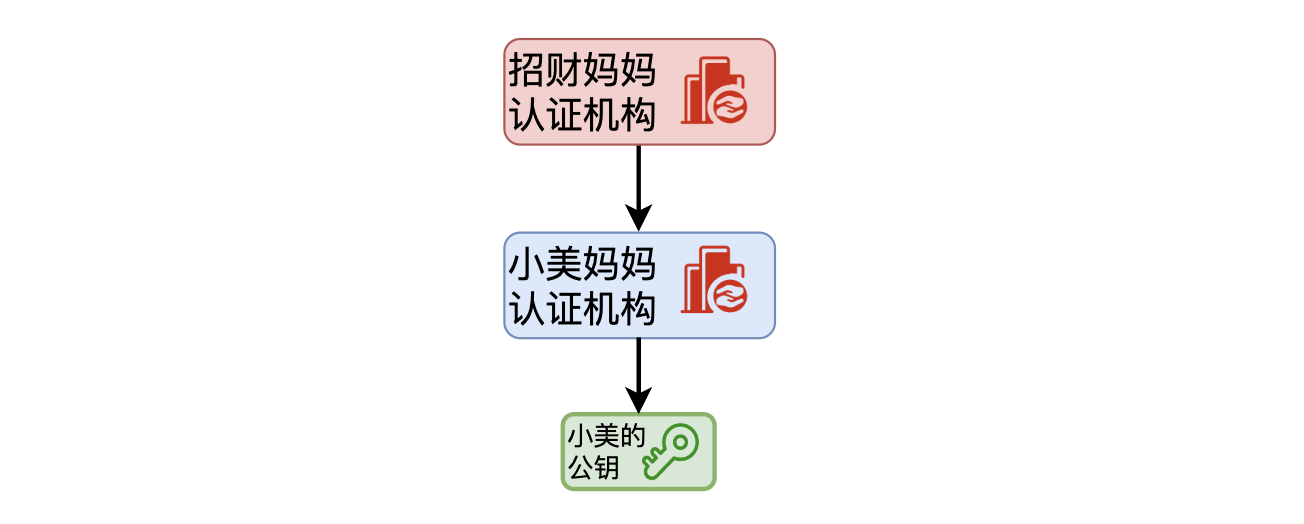
你看了一下这个层级,既然是你妈妈开的认证机构,你肯定选择信任,由于「招财妈妈认证机构」出具了「小美妈妈认证机构」公钥的证书,「小美妈妈认证机构」又出具了小美公钥的证书,根据这个信任链条,你自然就信任小美的公钥的合法性了。
到此,问题全部解决。
标签:小美,公钥,加密,摘要,秘钥,消息,设计 From: https://www.cnblogs.com/chanmufeng/p/17921392.html作者:蝉沐风,公众号:蝉沐风的码场