共轭梯度法
- 适应于求解非线性优化问题
- 线性共轭梯度法和非线性共轭梯度法
1 共轭方向
梯度下降法和共轭方向法优过程的区别:
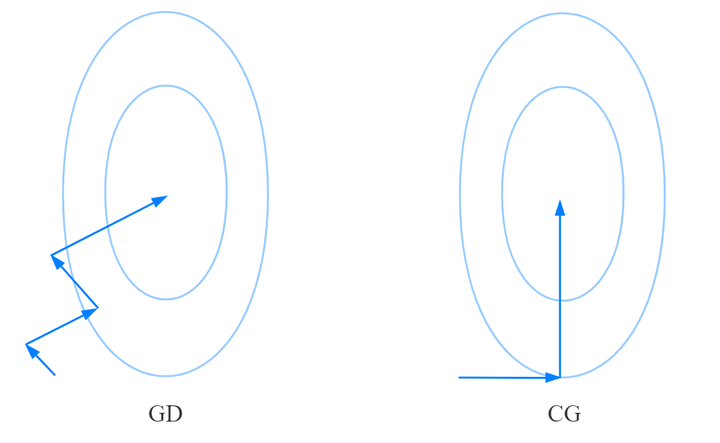
可以发现:
- 共轭方向法分别按两个轴的方向搜索(逐维搜索)
- 每次搜索只更新迭代点的一个维度
- 保证每次迭代的那个维度达最优
- 共轭方向法的两个搜索方向正交(特殊情况)
从正交推广到共轭
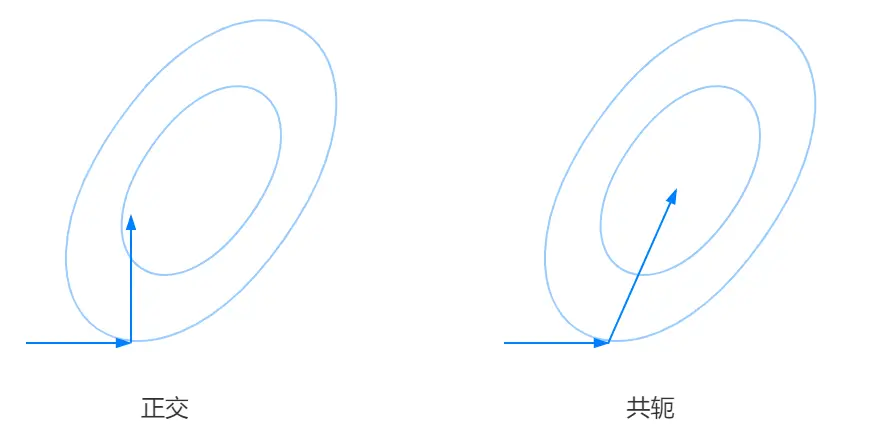
对比之前空间的 “椭圆” 可以直观的发现这里的 “椭圆” 倾斜了,如果按原来正方向的形式(特殊情况)选取搜索方向显然违背了共轭方向法的本意。
如果将原标准空间的 “椭圆” 的倾斜变换,视为其在空间的线性变换,同时让原来的搜索方向(正交)参与到这种空间的线性变换中,得到的结果可以如下图表示。
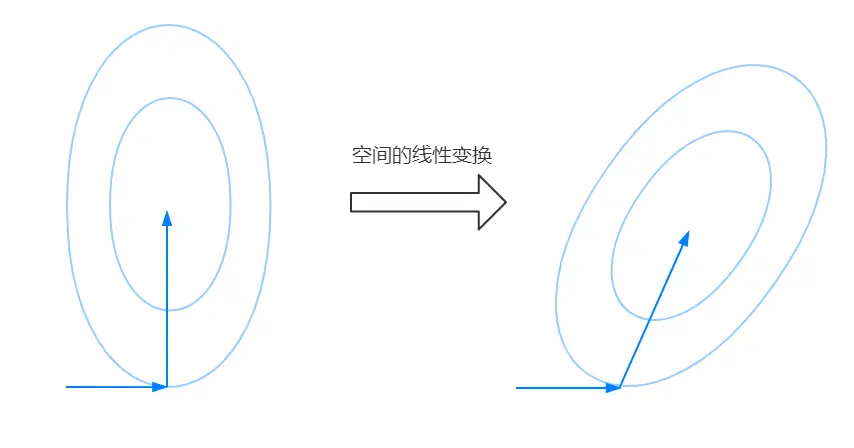
可以从上图发现原空间正交的两个搜索方向经过空间的线性变换后不再正交,但是和 “椭圆” (的轴)贴合的还是很好。如果将这种空间的线性变换描述为 \(Q\),那么可以说原度量空间 \(I\) 在线性变换后变成了 \(Q\),同时搜索方向 “沿轴搜索” 的性质依然存在。由于这种变换非仿射变换,所以原空间的 0 在 \(Q\) 度量的意义下还是 0 。
这时假设连个搜索方向为 \(d_1\) 和 \(d_2\),在原空间中 \(d_1\) 和 \(d_2\) 正交,即 \(d_1^T d_2 = 0\) 。经线性变换 \(Q\) 后 \(d_1^T d_2 = 0\) 变成 \(d_1^T Q d_2 = 0\) (这实际上就是共轭的表达式)
共轭的定义
设 \(Q\) 是正定矩阵,若对于两个不同的非零向量 \(d_i\) 和 \(d_j\) 满足:
\[d_i^T Q d_j = 0 \]则称 \(d_i\) 和 \(d_j\) 是共轭方向
共轭向量组
-
一组方向 \(d_0, d_1, \dots, d_{n-1}\) 中的任意两个向量 \(d_i\) 和 \(d_j\) 满足 \(d_i^T Q d_j = 0\)
-
共轭向量组中的向量一定线性无关
-
若 \(Q\) 是正定矩阵,则存在唯一的对称矩阵 \(A\) 使 \(Q = AA\),矩阵 \(A\) 也被称为矩阵 \(Q\) 的平方根
二次型的共轭方向
需要的共轭向量组就是目标二次型的 Hessian 矩阵的平方根逆矩阵的列向量组。
2 共轭方向法框架
① 给定迭代初值 \(x_0\) 和阈值 \(\epsilon > 0\),令 \(k = 0\)
② 计算 \(g_0 = \nabla f(x_0)\) 和初始下降方向,满足 \(d_0^Tg_0 < 0\)
③ Do while( 不满足 \(||g_k|| < \epsilon\) )
a. 线搜索确定步长:\(\alpha_k = \arg\min_\alpha f(x_k + \alpha d_k)\)
b. 更新迭代点:\(x_{k+1} = x_k + \alpha_k d_k\)
c. 采用某种共轭方法计算得到 \(d_{k+1}\),使得 \(d_{k+1}^T G d_j = 0, j = 0,1,\dots,k\)
d. 令 \(k = k + 1\)
end while
3 子空间扩展定理
- 第 \(k\) 次迭代时的方向与前面 \(k-1\) 次迭代得到的所有搜索方向正交
- 第 \(k\) 次得到的搜索方向正交于前面 \(k-1\) 次搜索方向张成的线性空间
- 每次迭代得到 \(d_k\) ,原子空间的维度便得到扩展,即 \(k-1\) 维的线性空间变成了 \(k\) 维
- \(G\) 是正定矩阵,\(d_i\) 和 \(d_j\) 关于 \(G\) 共轭,对于二次型 \(f(x) = \dfrac{1}{2} x^TGx - b^Tx\) :
- \(g_k = G x_k + b\)
- \(g_{k+1}^T d_j = 0, \;\; j = 0,1,\dots,k\)
- \(g_{k+1} - g_k = G(x_{k+1} - x_k) = \alpha_k G d_k\)
4 共轭梯度法
- 共轭梯度法是共轭方向法的一个方法
- 搜索方向的构造要求
- 所有的搜索方向相互共轭
- 搜索方向 \(d_k\) 仅仅是 \(-g_k\) 和 \(d_{k-1}\) 的线性组合
建立 \(d_k\) 和 \(d_{k-1}\) 的关系(共轭方向迭代公式):
\[d_k = -g_k + \beta_{k-1} d_{k-1} \]- \(g_k\) 是目标函数的梯度 \(\nabla f(x_{k})\)
- 注意上式无法得到第一个共轭方向,一般用 GD 获取,即梯度的反方向
确定 \(\beta_{k-1}\) 的算式
\(\beta_{k-1}\) 的确定可以使用共轭的性质,在上式两边同乘 \(d_{k-1}^T Q\),根据 \(d_{k-1}^T Q d_k = 0\) :
\[\beta_{k-1}^{HS} = \frac{g_k^T G d_{k-1}}{d_{k-1}^T G d_{k-1}} \quad \text{(Hestenes-Stiefel 公式)} \]\(\beta_{k-1}^{HS}\) 算式优化:由于 Hestenes-Stiefel 公式中有矩阵,因此可以进行优化让矩阵消失,目的是:
- 可以使共轭梯度法能适用于非二次型函数(形式上)
- 矩阵运算变成向量运算可以降低计算机计算的空间复杂度和时间复杂度
根据 \(g_{k+1} - g_k = G(x_{k+1} - x_k) = \alpha_k G d_k\) ,得:
\[\beta_{k-1}^{CW} = \frac{g_k^T(g_k-g_{k-1})}{d_{k-1}^T (g_k - g_{k-1})} \quad \text{(Crowder-Wolfe 公式)} \]\(\beta_{k-1}^{CW}\) 算式优化:让式中只出现梯度信息(常用的有 FR 和 PRP)
根据 \(g_{k+1}^T d_j = 0, \;\; j = 0,1,\dots,k\) ,有 \(g_{k+1} g_k = 0\) ,得:
\[\beta_{k-1}^{FR} = \frac{g_k^T g_k}{g_{k-1}^T g_{k-1}} \quad \text{(Fletcher-Reeves 公式)} \]共轭方向迭代公式(FR):
\[d_k = -g_k + \beta_{k-1} ^{FR} d_{k-1} \]计算步长 \(\alpha_k\):
根据之前推导 \(\beta_{k-1}\) 的结论可以得出:
\[\alpha_k = \frac{g_k^T g_k}{d_k^T G d_k} \]5 共轭梯度法算法(CG-FR)
- 适用于线性和非线性函数
① 给定迭代初始点 \(x_0\),迭代终止阈值 \(\epsilon\)
② 令初始梯度 \(g_0 = Gx_0 - b\),初始搜索方向 \(d_0 = -g_0\),迭代次数 \(k = 0\)
③ Do while( \(||g_k|| > \epsilon\) ) {
a. 计算步长:\(\alpha_k = \dfrac{g_k^T g_k}{d_k^T G d_k}\)
b. 更新迭代点:\(x_{k+1} = x_k + \alpha_k d_k\)
c. 计算新的梯度:\(g_{k+1} = g_k + \alpha_k G d_k\)
d. 计算组合系数:\(\beta_{k+1}^{FR} = \dfrac{g_{k+1}^T g_{k+1}}{g_k^T g_k}\)
e. 计算新的搜索方向:\(d_{k+1} = -g_{k+1} + \beta_{k+1}^{FR} d_k\)
f. 令 \(k = k + 1\) }
end while
5 线性共轭梯度法
- 一种求解具有正定系数矩阵的线性系统的迭代方法
- 是高斯消去法的一种替代方法,适合解决大型问题
- 性能取决于系数矩阵特征值的分布
- 线性系统进行预处理可以使这种分布更加有利
- 线性系统进行预处理可以提高方法的收敛性
6 非线性共轭梯度法
- 有多种变体
- 算法的主要特点
- 不需要矩阵存储
- 比最速下降法更快
标签:迭代,梯度,beta,搜索,方向,共轭 From: https://www.cnblogs.com/J-Chow/p/17905048.html