1.题目介绍

给你一个二叉树的根节点 \(root\) ， 检查它是否轴对称。

示例 1：

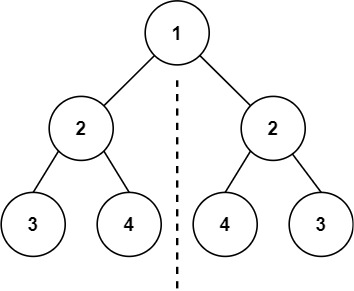
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

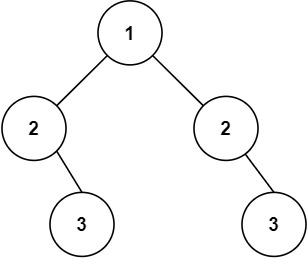
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 \([1, 1000]\) 内
• \(-100 <= Node.val <= 100\)

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

2.题解

2.1 递归

思路

这里的思路是进行递归搜索，p和q分别走左右两个子树。p向左走看当前节点左子树，q就向右走看当前节点右子树，反之同理。
如果当前节点值均相同说明二叉树对称。反之出现不等值，或者某一子树先行结束说明非对称二叉树

代码

class Solution {
public:
    bool check_mirror(TreeNode* p, TreeNode* q){
        if (!p && !q) return true;
        if (!p || !q) return false;
        return p->val == q->val && check_mirror(p->left, q->right) && check_mirror(p->right,q->left);
    }

    bool isSymmetric(TreeNode* root) {
        if (root == nullptr) return true;
        return check_mirror(root,root);
    }
};

2.2迭代

思路

使用队列存储每层节点，由于其先进先出的特性，每次定是先遍历完一层再进入下一层进行搜寻。
存储的时候采用交错存储来对应二叉树镜像，这边存储一节点的左子节点，接下来就存储对应镜像节点的右子节点（保证镜像性）
并进行结束条件和值是否相等的比较。

代码

class Solution {
public:
    bool check_mirror(TreeNode* root){
        queue<TreeNode*> q;
        q.push(root); q.push(root);
        while (!q.empty()){
            TreeNode* left = q.front(); q.pop();
            TreeNode* right = q.front(); q.pop();
            if (!left && !right) continue;
            if (!left || !right || (left->val != right ->val)) return false;
            q.push(left->left);
            q.push(right->right);
            q.push(left->right);
            q.push(right->left);
        }
        return true;
    }

    bool isSymmetric(TreeNode* root) {
        if (root == nullptr) return true;
        return check_mirror(root);
    }
};;