CF1737C Ela and Crickets

题意

给定一个 \(n\times n\) 的棋盘，棋盘上有且仅有三颗排成 \(\text{L}\) 形的棋子。

对于 \(\text{L}\) 形的定义，有且仅有以下四种情况：

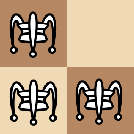
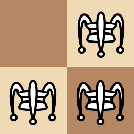
棋子的移动规则和跳棋相同。它可以水平、垂直或斜向移动。当且仅当一个棋子的某个方向紧随另一个棋子时，它能跳到另一个棋子之后的一个方格上。棋子不能跳出棋盘。

现在有 \(T\) 组询问，每组给出棋盘大小 \(n(n\le 10^5)\)，三颗棋子各自的位置 \(r_1,c_1,r_2,c_2,r_3,c_3(1\le r_1,c_1,r_2,c_2,r_3,c_3 \le n)\)，以及目标点 \(x,y(1 \le x,y \le n)\)，询问是否能使其中的一颗棋子跳到目标点。输出 YES 或 NO。

思路

不要想太复杂，这题其实就是个分支语句

现在有这种情况：

咱们进行若干次操作如图：（绿色是被操作的，黄色是操作后的）

可以发现，上图中我们通过若干次操作将原图形向左进行了平移。

那么，也可以用同样的方法向另外四个方向进行平移。

所以，我们可以得出结论：通过若干次操作，我们就可以将原图形进行平移，得到新的图形。将L形看作一个 \(2\times 2\) 的正方形，那么无法走到的就是L形的缺口，所以我们只需要判断一下目标点是不是平移若干次后L形的缺口即可。

具体的，如图，我们通过操作一定平移不到蓝色方块处：

更具体的，如果该 \(2 \times 2\) 的方块中空白的点坐标为 \((r,c)\) ，那么他就一定无法移动到 \((x,y)\) 满足 \(x \equiv r \bmod 2, y \equiv c \bmod 2\)

需要注意，如果L形是在四个角上，那么这种情况较为特殊，需要特判一下

代码

如果中间那段map查找换成直接判断的话，那这题就变成一道纯分支语句的1500了（）

#include<bits/stdc++.h>
using namespace std;
int r,c,r1,c1;
    //r表示L形的竖边所在的列，c表示L形横边所在的行
    //(r1,c1)表示L形缺口的坐标
int x,y,n;
void run()
{
    map<int,int>fr,fc;
    cin>>n;
    for(int i=1;i<=3;i++)
    {
        cin>>r>>c;
        fr[r]++;
        fc[c]++;
    }
    cin>>x>>y;
    for(auto it=fr.begin();it!=fr.end();it++) 
    {
        if(it->second==2) r=it->first;
        else if(it->second==1) r1=it->first;
    }
    for(auto it=fc.begin();it!=fc.end();it++)
    {
        if(it->second==2) c=it->first;
        else if(it->second==1) c1=it->first;
    }
    //L形缺口的坐标就是三组(r,c)中只出现一次的，而横竖遍则分别出现了两次，据此map查找即可
    //这里为了方便用了map，你手动分支语句也可以
    if(r==1 && c==1) 
    {
        if(x==1 || y==1) cout<<"Yes";
        else cout<<"No";
    }else if(r==1 && c==n) 
    {
        if(x==1 || y==n) cout<<"Yes";
        else cout<<"No";
    }else if(r==n && c==1) 
    {
        if(x==n || y==1) cout<<"Yes";
        else cout<<"No";
    }else if(r==n && c==n) 
    {
        if(x==n || y==n) cout<<"Yes";
        else cout<<"No";
    }else
    {
        if(x%2==r1%2 && y%2==c1%2) cout<<"No";
        else cout<<"Yes";
    }
    cout<<endl;
}
int main()
{
    int t;
    cin>>t;
    while(t--) run();
}