力扣2477. 到达首都的最少油耗(dfs+贪心）

给你一棵 n 个节点的树（一个无向、连通、无环图），每个节点表示一个城市，编号从 0 到 n - 1 ，且恰好有 n - 1 条路。0 是首都。给你一个二维整数数组 roads ，其中 roads[i] = [ai, bi] ，表示城市 ai 和 bi 之间有一条 双向路 。

每个城市里有一个代表，他们都要去首都参加一个会议。

每座城市里有一辆车。给你一个整数 seats 表示每辆车里面座位的数目。

城市里的代表可以选择乘坐所在城市的车，或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。

请你返回到达首都最少需要多少升汽油。

示例 1：

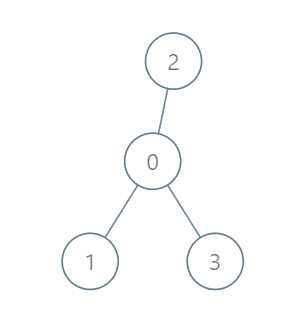
输入：roads = [[0,1],[0,2],[0,3]], seats = 5
输出：3
解释：
- 代表 1 直接到达首都，消耗 1 升汽油。
- 代表 2 直接到达首都，消耗 1 升汽油。
- 代表 3 直接到达首都，消耗 1 升汽油。
最少消耗 3 升汽油。

示例 2：

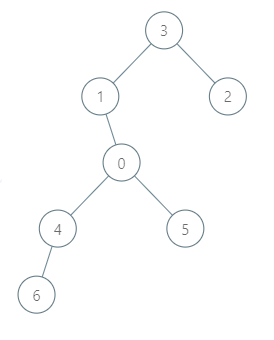
输入：roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
输出：7
解释：
- 代表 2 到达城市 3 ，消耗 1 升汽油。
- 代表 2 和代表 3 一起到达城市 1 ，消耗 1 升汽油。
- 代表 2 和代表 3 一起到达首都，消耗 1 升汽油。
- 代表 1 直接到达首都，消耗 1 升汽油。
- 代表 5 直接到达首都，消耗 1 升汽油。
- 代表 6 到达城市 4 ，消耗 1 升汽油。
- 代表 4 和代表 6 一起到达首都，消耗 1 升汽油。
最少消耗 7 升汽油。

示例 3：

输入：roads = [], seats = 1
输出：0
解释：没有代表需要从别的城市到达首都。

提示：

• 1 <= n <= 105
• roads.length == n - 1
• roads[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• roads 表示一棵合法的树。
• 1 <= seats <= 105

知道应该用贪心，但还是没有局部考虑，宏观考虑很难得想象出贪心策略，只有把模型抽象到：从一个站到下一站，一共有多少人，需要几辆车。每次仅计算两个相邻节点之间的用车数，就可以完美解决这个问题。我这个代码耗时比较长，应该是用了map的原因，比题解的vector慢非常多。

 1 class Solution {
 2 public:
 3     bool flag[100005];
 4     map<int,vector<int>> m;
 5     long long sum = 0;
 6     int dfs(int station, int seats){ //该dfs的目的在于求出经过station站的代表总数，即子节点总数
 7         if (!flag[station]){
 8             flag[station] = true;
 9             int childNumber = 1; //station站会经过的代表总数，每站有一名代表，初值为1.
10             for (auto i : m[station]){
11                 if (!flag[i]){
12                     int peopleNumber = dfs(i,seats);
13                     sum += (peopleNumber + seats - 1) / seats;//上一站到达该站需要的车辆数，向上取整
14                     childNumber += peopleNumber; 
15                 }
16             }
17             return childNumber;
18         }
19         return 0;
20     }
21     long long minimumFuelCost(vector<vector<int>>& roads, int seats) {
22         memset(flag, false, sizeof(flag));
23         for (auto i : roads){
24             m[i[0]].push_back(i[1]);
25             m[i[1]].push_back(i[0]);
26         }
27         dfs(0,seats);
28         return sum;
29     }
30 };