# Lab1_简单集群搭建
## 实验记录
实验环境:Vmware 下的 CentOS7.6 拟机
### 单机配置环境
参考资料:[上海大学计算机体系结构实验四 HPL安装和测试](https://blog.csdn.net/qq_51413628/article/details/130628390)
#### 1、安装、编译 BLAS、CBLAS
首先下载 gcc 和 gfortran ,完成后下载后先对 BLAS 进行编译,获得 blas_LINUX.a 文件并链接 *.o 文件生成 libblas.a;后使用此生成文件修改 CBLAS 的 Makefile 文件并编译 CBLAS。最后把库文件丢到 `/usr/local/lib` 中方便以后获取。

#### 2、安装 MPI
测试的时候发现使用 openmpi 一直会使 hpl 编译失败,还未开始找问题,先使用 mpich 进行实验。
使用 `./configure --prefix=/home/mpich-install` 修改安装路径,随后是时间比较长的安装过程。
安装完成后,在 PATH 参数中添加 bin 路径。
#### 3、安装 hpl
在 hpl 的 `/setup` 文件夹下选择一个 Make 文件,此处选择的是 `Make.Linux_PII_CBLAS` 。复制到 hpl 目录下进行参数配置并编译,在 `/bin/Linux_PII_CBLAS` 文件夹下生成 `xhpl` 文件用于运行。

### 搭建集群
参考资料:[基于VMWare虚拟机搭建Linux集群](https://blog.csdn.net/weixin_37957321/article/details/105478657)
这里使用四台虚拟机,分别取名 Serv ClinOne ClinTwo ClinThree;最终在 Serv 机上进行最终测试。
#### 1、配置 Serv 端、克隆 Clin 端
按照文章修改虚拟机网卡设置、在虚拟机和本机上添加 hosts 地址;之后对克隆出来的虚拟机依次进行修改,最后配置 ssh 并关掉防火墙。
#### 2、进行测试
配置 HPL.dat 文件:

主要修改进程组合方式 p q 、矩阵规格。
配置 hostfile 文件:

运行测试并记录数据:
| N | NB | P Q | Time | Gflops |
| ---- | ---- | ---- | ---- | ------ |
| 1960 | 60 | 1 4 | 1.08 | 4.6718 |
| 1960 | 80 | 1 4 | 1.16 | 4.3150 |
| 2048 | 60 | 1 4 | 1.24 | 4.6361 |
| 2048 | 80 | 1 4 | 1.41 | 4.0662 |
| 1960 | 60 | 2 2 | 1.50 | 3.3396 |
| 1960 | 80 | 2 2 | 1.52 | 3.3168 |
| 2048 | 60 | 2 2 | 1.47 | 3.9069 |
| 2048 | 80 | 2 2 | 1.55 | 3.7036 |
| 1960 | 60 | 4 1 | 2.98 | 1.6854 |
| 1960 | 80 | 4 1 | 3.04 | 1.6558 |
| 2048 | 60 | 4 1 | 3.33 | 1.7240 |
| 2048 | 80 | 4 1 | 3.33 | 1.7227 |
| N | NB | P Q | Time | Gflops |
| ---- | ---- | ---- | ---- | ------ |
| 1960 | 60 | 1 1 | 2.37 | 2.1227 |
| 1960 | 80 | 1 1 | 2.42 | 2.0787 |
| 2048 | 60 | 1 1 | 2.69 | 2.1318 |
| 2048 | 80 | 1 1 | 2.69 | 2.1328 |
| 1960 | 60 | 1 2 | 1.54 | 3.2631 |
| 1960 | 80 | 1 2 | 1.50 | 3.3553 |
| 2048 | 60 | 1 2 | 1.75 | 3.2733 |
| 2048 | 80 | 1 2 | 1.68 | 3.4156 |
| 1960 | 60 | 1 4 | 1.08 | 4.6718 |
| 1960 | 80 | 1 4 | 1.16 | 4.3150 |
| 2048 | 60 | 1 4 | 1.24 | 4.6361 |
| 2048 | 80 | 1 4 | 1.41 | 4.0662 |
发现运行速度和 CPU 数量成正比,且一般情况下 CPU 数量一定时,在 p 更小的时候能获得更优的性能。
搜索发现有两点原因,一是矩阵运算中行优先(P<Q)能增加内存块地连续性、更频繁地访问临近数据,从而优化缓存使用;二是在 HPL 计算过程中会频繁进行行通信和列通信,而 P<Q 能更多地使用进程数量更少的行通信。
为了观察网络通信对性能的影响,再尝试在单个虚拟机上测试:
| N | NB | P Q | Time | Gflops |
| ---- | ---- | ---- | ---- | ------ |
| 1960 | 60 | 4 1 | 1.06 | 4.7606 |
| 1960 | 80 | 4 1 | 1.15 | 4.3577 |
| 2048 | 60 | 4 1 | 1.04 | 5.5255 |
| 2048 | 80 | 4 1 | 1.05 | 5.4641 |
| 1960 | 60 | 2 2 | 0.77 | 6.5558 |
| 1960 | 80 | 2 2 | 0.78 | 6.4136 |
| 2048 | 60 | 2 2 | 0.90 | 6.3783 |
| 2048 | 80 | 2 2 | 0.87 | 6.5609 |
| 1960 | 60 | 4 1 | 0.75 | 6.6664 |
| 1960 | 80 | 1 4 | 0.83 | 6.0415 |
| 2048 | 60 | 1 4 | 0.87 | 6.5785 |
| 2048 | 80 | 1 4 | 0.91 | 6.3041 |
发现拓宽通信瓶颈之后性能明显提升且不再明显与 Q 成正比。在通信开销小、节点强大的场景中,更大的 P 可以得到更好的计算性能。
Lab2
代码
截取的 vectorized 函数部分:
def bilinear_interp_vectorized(a: np.ndarray, b: np.ndarray) -> np.ndarray:
"""
This is the vectorized implementation of bilinear interpolation.
- a is a ND array with shape [N, H1, W1, C], dtype = int64
- b is a ND array with shape [N, H2, W2, 2], dtype = float64
- return a ND array with shape [N, H2, W2, C], dtype = int64
"""
# get axis size from ndarray shape
N, H1, W1, C = a.shape
N1, H2, W2, _ = b.shape
assert N == N1
res = np.empty((N, H2, W2, C),dtype = int64)
# TODO: Implement vectorized bilinear interpolation
b_idx = np.floor(b).astype(int)
b_res = b - b_idx
res = a[np.arange(N)[:, None, None], b_idx[:, :, :, 0], b_idx[:, :, :, 1]] * (1 - b_res[:, :, :, 0, None]) * (1 - b_res[:, :, :, 1, None]) + \
a[np.arange(N)[:, None, None], b_idx[:, :, :, 0]+1, b_idx[:, :, :, 1]] * b_res[:, :, :, 0, None] * (1 - b_res[:, :, :, 1, None]) +\
a[np.arange(N)[:, None, None], b_idx[:, :, :, 0], b_idx[:, :, :, 1]]+1 * (1 - b_res[:, :, :, 0, None]) * b_res[:, :, :, 1, None] +\
a[np.arange(N)[:, None, None], b_idx[:, :, :, 0]+1, b_idx[:, :, :, 1]+1] * b_res[:, :, :, 0, None] * b_res[:, :, :, 1, None]
return res
实验报告
思路
主要是在代码的正确性上下功夫。
最开始想追求直接以长度为 \(C\) 的向量为基本单位进行运算,但是发现直接以单个数字运算基本不存在性能差异。
通过在 IDLE 中不断尝试,最终得到了正确的广播格式代码如上。
正确性 & 加速比
关于 Numpy 的广播
Lab2.5
代码片段
for(int i=0;i<MAXN;i+=8)
{
__m256 va = _mm256_loadu_ps(&a[i]);
__m256 vb = _mm256_loadu_ps(&b[i]);
__m256 result = _mm256_mul_ps(va, vb);
__m256 vc = _mm256_loadu_ps(&c[i]);
vc = _mm256_add_ps(vc, result);
_mm256_storeu_ps(&c[i], vc);
}
for(int i=MAXN-MAXN%8;i<MAXN;i++)
c[i] += a[i]*b[i];
运行结果
汇编程序阅读
SIMD 汇编程序部分代码:
0x00000000004018ba <+906>: vmovups ymm0,YMMWORD PTR [rax]
0x00000000004018be <+910>: vmovaps YMMWORD PTR [rbx+0xe0],ymm0
0x00000000004018c6 <+918>: vmovaps ymm0,YMMWORD PTR [rbx+0x100]
0x00000000004018ce <+926>: vmovaps YMMWORD PTR [rbx+0x80],ymm0
0x00000000004018d6 <+934>: vmovaps ymm0,YMMWORD PTR [rbx+0xe0]
0x00000000004018de <+942>: vmovaps YMMWORD PTR [rbx+0x60],ymm0
=> 0x00000000004018e3 <+947>: vmovaps ymm0,YMMWORD PTR [rbx+0x80]
0x00000000004018eb <+955>: vmulps ymm0,ymm0,YMMWORD PTR [rbx+0x60]
0x00000000004018f0 <+960>: vmovaps YMMWORD PTR [rbx+0xc0],ymm0
可以看到,这里使用了 YMMWORD 类型的指针。经过查阅发现 YMMWORD 的长度是 256 位,表明一条指令相比于普通程序可以同时操作多个数据进行运算。
向量化计算
Numpy 库
NumPy 是 Python 中科学计算的基础包。它是一个 Python 库,提供多维数组对象,各种派生对象(如掩码数组和矩阵),以及用于数组快速操作的各种 API,有包括数学、逻辑、形状操作、排序、选择、输入输出、离散傅立叶变换、基本线性代数,基本统计运算和随机模拟等等。
Numpy 代码一般采用向量化(矢量化)描述,这使得代码中没有任何显式的循环,索引等,这样的代码有以下好处:
- 向量化代码更简洁,更易于阅读
- 更少的代码行通常意味着更少的错误
- 代码更接近于标准的数学符号
另外,向量化的代码能够规避掉 Python 中缓慢的迭代循环,被底层的实现更好的调度,如接入 BLAS 矩阵运算库,从而实现更高的性能。
n-dimensional array
ndarray 是 Numpy 库中的核心概念,不管 n 是多少,对 ndarray 的操作在代码形式上基本相同。
Numpy Array 和 Python List 的区别
主要是在做计算。
>>> a = np.array([1,2,3])
>>> a * 2
array([2,4,6])
当维数超过 1 时,Numpy Array 的表现要更好;但需要注意 Array 中的元素类型需要相同。

使用
Numpy Array 不能像 list 那样进行 insert 操作,需要初始化时就做好规划。
1 dimensional
初始化
直接使用 python list 转化。注意元素类型一致。
b = np.zeros(3, int) # b.dtype == np.int32
c = np.zeros_like(a) # c.dtype == a.dtype, c.shape == a.shape
#事实上,_like 尾缀很常用。
np.ones(3) => np.ones_like(a)
np.empty(3) => np.empty_like(a)
np.full(3,7.) => np.full_like(a,7)
更多初始化方法:



数组索引
a = np.arange(1, 6)
a => ([1,2,3,4,5])
a[1] => ([2])
a[2:4] => ([3,4])
a[-2:] => ([4,5])
a[::2] => ([1,3,5])
a[[1,3,4]] => ([2,4,5]) #fancy indexing
注意取向量的一部分时指针是否指向原始数据!!!一般来说,只有 fancy indexing 会在某种情况下复制原始数据。
向量操作
最喜欢的一集。请欣赏。





可以看到对于具体实现操作,更多的是对每个数值进行操作。这与 for 循环类似,但是 Numpy 通过某些方法可以使得这些过程比一般的 for 循环要快。而且基本上所有操作都支持隐式 for 循环,如三角函数等。
除此之外,还有 sort、reverse 等。
2 dimensional
The axis argument
对于 sum 之类会操作某一行的函数,使用 a.sum(axis=0) , 其中 0 表示被操作的轴是 0。
双线性插值算法
\[x_1\leq x \leq x_2 \\ y_1\leq y \leq y_2 \\ 现知道\ f(x,y)\ 在 (x_1,y_1) (x_1,y_2) (x_2,y_1)(x_2,y_2) 的取值,要估计 f(x,y)。 \]\[\begin{aligned} f(x,y) &= \frac{x-x_1}{x_2-x_1} f(x_2,y)+\frac{x_2-x}{x_2-x_1}f(x_1,y) \\ &= \frac{x-x_1}{x_2-x_1}(\frac{y-y_1}{y_2-y_1}f(x_2,y_2)+\frac{y_2-y}{y_2-y_1}f(x_2,y_1)) + \frac{x_2-x}{x_2-x_1}(\frac{y-y_1}{y_2-y_1}f(x_1,y_2)+\frac{y_2-y}{y_2-y_1}f(x_1,y_1)) \\ &= \frac1{(x_2-x_1)(y_2-y_1)} (写不出来) \end{aligned} \]向量化计算
一份使用 for 循环的 python 代码:
def bilinear_interp_baseline(a: np.ndarray, b: np.ndarray) -> np.ndarray:
"""
This is the baseline implementation of bilinear interpolation without vectorization.
- a is a ND array with shape [N, H1, W1, C], dtype = int64
- b is a ND array with shape [N, H2, W2, 2], dtype = float64
- return a ND array with shape [N, H2, W2, C], dtype = int64
"""
# Get axis size from ndarray shape
N, H1, W1, C = a.shape
N1, H2, W2, _ = b.shape
assert N == N1
# Do iteration
res = np.empty((N, H2, W2, C), dtype=int64)
for n in range(N):
for i in range(H2):
for j in range(W2):
x, y = b[n, i, j]
x_idx, y_idx = int(np.floor(x)), int(np.floor(y))
_x, _y = x - x_idx, y - y_idx
# For simplicity, we assume:
# - all x are in [0, H1 - 1)
# - all y are in [0, W1 - 1)
res[n, i, j] = a[n, x_idx, y_idx] * (1 - _x) * (1 - _y) + \
a[n, x_idx + 1, y_idx] * _x * (1 - _y) + \
a[n, x_idx, y_idx + 1] * (1 - _x) * _y + \
a[n, x_idx + 1, y_idx + 1] * _x * _y
return res
这里对于 \(N\) 个数据分别进行 \(H_2\times W_2\) 次向量长度为 \(C\) 的插值运算,给出每次运算时需要的 \(x\) 和 \(y\) 。
\[\begin{aligned} res_{n,i,j} &= \begin{bmatrix} 1-x&x \end{bmatrix} \begin{bmatrix} a_{n,x_0,y_0}&a_{n,x_0,y_0+1}\\a_{n,x_0+1,y_0}&a_{n,x_0+1,y_0+1} \end{bmatrix} \begin{bmatrix}1-y\\y\end{bmatrix} \end{aligned} \]\[res_{n,i,j} = a_{n,b\_idx_{n,i,j}} \]Cuda
引入例子
现在我们在 C++ 中进行两个数列的加和操作:
void add(int n, float *x, float *y)
{
for (int i = 0; i < n; i++)
y[i] = x[i] + y[i];
}
现在,我想让这段代码运行在 GPU 上("kernel" in Cuda)。我们要做的就是给函数加一个 __global__ 标记。
__global__
void add(int n, float *x, float *y)
{
for (int i = 0; i < n; i++)
y[i] = x[i] + y[i];
}
这些 __global__ 函数叫做 kernels ,而在 GPU 上跑的代码叫做 kernel code,CPU 上跑的代码叫 host code。
内存分配
需要给 GPU 分配其可以使用的内存。
Unified Memory
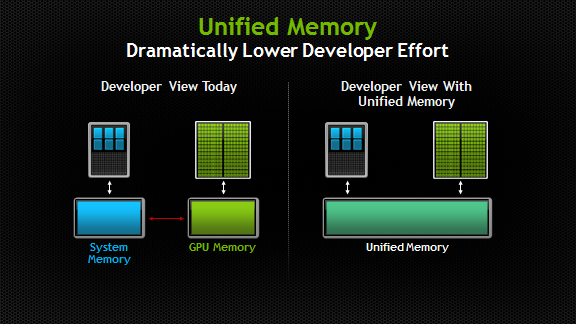
在代码中声明 Unified Memory 的方式:
float *x, *y;
cudaMallocManaged(&x, N*sizeof(float));
cudaMallocManaged(&y, N*sizeof(float));
// Free memory
cudaFree(x);
cudaFree(y);
同时,注意 CPU 还需要等 GPU 跑完才能获取结果,这需要使用 cudaDeviceSynchronize() 函数。
// Run kernel on 1M elements on the GPU
add<<<1, 1>>>(N, x, y);
// Wait for GPU to finish before accessing on host
cudaDeviceSynchronize();
并行运算
这里 add<<<i, j>>>(N, x, y) 中 \(i\) 和 \(j\) 表示的即为 GPU 上的并行规模。具体来说, GPU 的结构是 \(grid\ \rightarrow\ block\ \rightarrow\ thread\) 的模式。
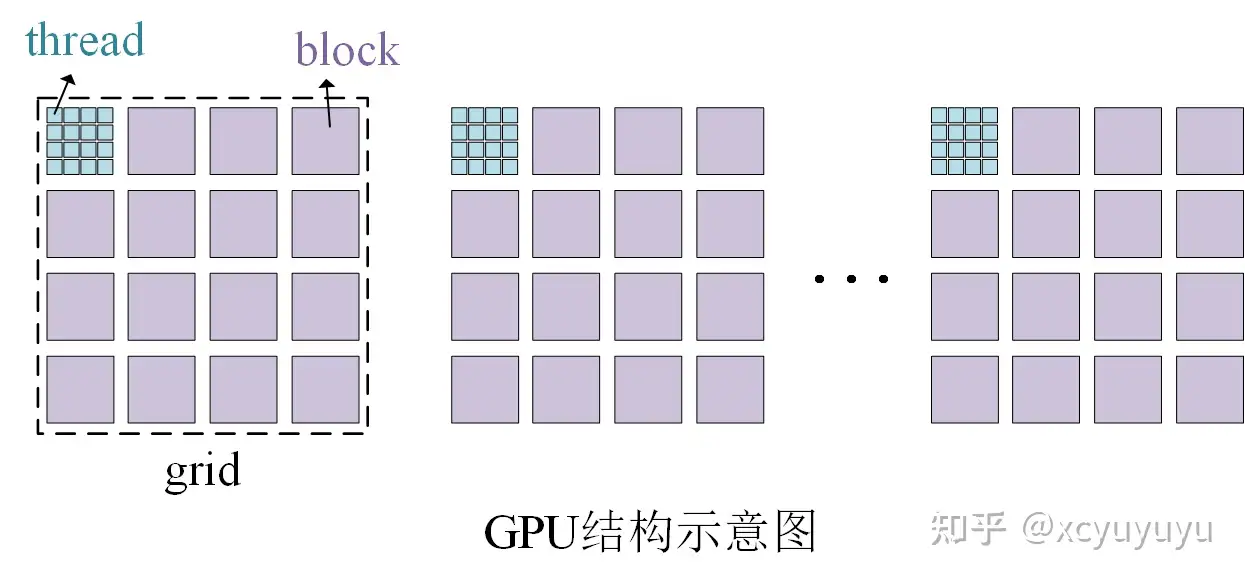
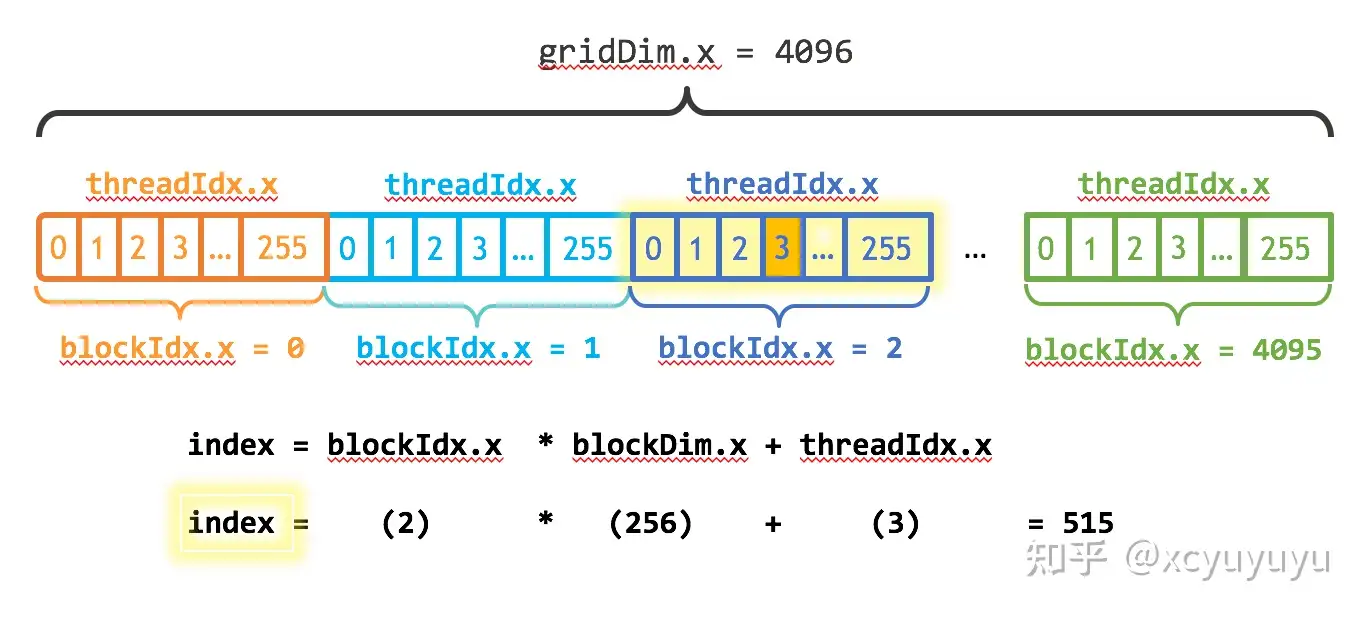
其中 \(i \leftarrow numBlocks\,,\ j \leftarrow blockSize\) 。同时,Cuda 的 GPU 使用大小为 32 的倍数的线程块运行内核,因此 \(blockSize\) 的大小应该设置为 32 的倍数。这之后,可以根据 for 循环的总个数来确定 \(numBlock\) 的大小:
int numBlocks = (N+blockSize-1) / blockSize;
此时,我们的 add 函数应该这样写:
void add( int n , float *x , float *y )
{
int index = blockIdx.x * blockDim.x + threadIdx.x;
int stride = blockDim.x * gridDim.x;
for(int i = index; i < n; i += stride)
y[i] = y[i] + x[i];
}
完整代码:
#include<iostream>
#include<math.h>
__global__
void add(int n, float *x, float *y)
{
int index = blockIdx.x * blockDim.x + threadIdx.x;
int stride = blockDim.x * gridDim.x;
for (int i = index; i < n; i+=stride)
y[i] = x[i] + y[i];
}
int main()
{
int N = 1<<25;
float *x, *y;
cudaMallocManaged(&x, N*sizeof(float));
cudaMallocManaged(&y, N*sizeof(float));
for(int i = 0; i < N; i++)
x[i] = 1.0f, y[i] =2.0f;
int blockSize = 256; //一个 block 中含有的 thread 数量。
int numBlock = (N + blockSize - 1) / blockSize;
add<<<blockSize,numBlock>>>(N,x,y);
cudaDeviceSynchronize();
float maxError = 0.0f;
for(int i = 0; i < N; i++)
maxError = fmax( maxError , fabs(y[i]-3.0f) );
printf("MAX error:%f\n", maxError);
cudaFree(x);
cudaFree(y);
return 0;
}
安装
GPU 总览
GPU 可以用来处理图形和并行计算。
一个 GPU (以 Nvidia Ampere 架构为例)包含:
- 8 GPC and 16 SM/GPC and 128 SMs per full GPU.
- 6 HBM2 stacks and 12 512-bit Memory Controllers.

Streaming Multiprocessor
简称 SM,其中有一些处理单元、内存缓存和一些控制逻辑。在深度学习中,SM 尤其重要,因为它可以同时处理大量矩阵运算,这对于神经网络训练等计算密集型任务非常关键。可以把其当作 GPU 的一个小引擎,负责执行并行任务。一个 SM 包含:
- 4 processing block/SM, 1 Warp scheduler/processing block.
- 64 INT32 CUDA Cores/SM, 64 FP32 CUDA Cores/SM, 32 FP64 CUDA Cores/SM.
- 192 KB of combined shared memory and L1 data cache.
- 4 Tensor Cores/SM

warp
一个 block 在一个 SM 上执行,并在执行时进一步被细分为 warp。每个 warp 一次可以处理 32 threads。为了提高利用率,推荐按照 warp 进行块的划分。
Shared Memory
注意其与 Unified Memory 的区分。
Bank
存储器并行访问:
一个具有4个 bank 的存储器:
Bank 0 Bank 1 Bank 2 Bank 3 Mem[0] Mem[1] Mem[2] Mem[3] Mem[4] Mem[5] Mem[6] Mem[7] Mem[8] Mem[9] Mem[10] Mem[11] \(\cdots\) \(\cdots\) \(\cdots\) \(\cdots\) 如果同一时间访问 Mem[0], Mem[9], Mem[6], Mem[3] 的存储空间;否则连续的访问序列位于同一 Bank,则效率就会降低。
但是如果存储器的 bank 进行过针对性优化,多个线程访问同一 bank 的同一位置可以通过同时向所有线程广播数据进行解决,则不会产生 bank conflict 的问题。
Tensor Core
高效浮点运算相关。
局部性
众所周知,由于缓存的存在,CPU 倾向于以更快的速度获取在时间上或者空间上距离我们较近的数据,这就是局部性。但是如何理解局部性?怎样使用局部性?我们考虑矩阵乘法。
朴素
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
c[i][j] += a[i][k] * b[k][j];
//time:5.101s for size=1024
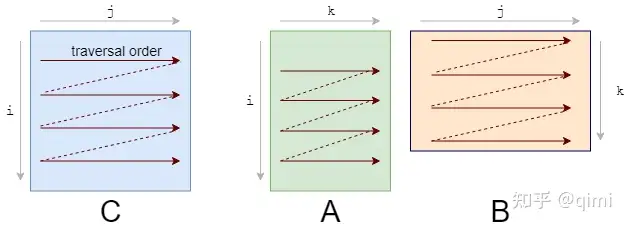
循环重排序
for (int i = 0; i < M; i++)
for (int k = 0; k < K; k++)
for (int j = 0; j < N; j++)
C[i][j] += A[i][k] * B[k][j]
//time:2.857s for size=1024
显然此时 A B C 的空间局部性都得到了保证。
分块
for(int I=0;I<block_num;I++)
for(int J=0;J<block_num;J++)
for(int K=0;K<block_num;K++)
for(int i=0;i<block_size;i++)
for(int k=0;k<block_size;k++)
for(int j=0;j<block_size;j++)
c(I*block_size+i,J*block_size+j) +=
a(I*block_size+i,K*block_size+k) *
b(K*block_size+k,J*block_size+j);
//time:5.298s for size=1024
转置
int *d = (int *)malloc((size*size+1)*sizeof(int));
for(int i=0;i<size;i++) for(int j=0;j<size;j++)
d(i,j) = b(j,i);
for(int i=0;i<size;i++)
for(int j=0;j<size;j++)
for(int k=0;k<size;k++)
c(i,j) += a(i,k) * d(j,k);
//time:2.833s for size=1024
//这里想体现的是转置比循环重排序的表现更加优秀一点。
实验记录
任务
输入 \(A,B,n\),计算:
\[\prod_{k=0}^nA+kB = A (A + B) (A+2B)\dots(A+nB) \]在本实验中,baseline.cu 代码中给出了实现的大部分,我们只需要修改函数 MultipleCudaKernel 和 MultipleCuda 即可。
阅读代码
//column 16 #define CUDA_CALL(func) \ { \ cudaError_t e = (func); \ if (!(e == cudaSuccess || e == cudaErrorCudartUnloading)) \ { \ fprintf(stderr, "CUDA: %s:%d: error: %s\n", __FILE__, __LINE__, \ cudaGetErrorString(e)); \ abort(); \ } \ }这一段代码定义了一个调用 Cuda 函数的方法,使得程序可以在函数出现问题时终止程序运行。
//column 26 #define CUBLAS_CALL(func) \ { \ cublasStatus_t e = (func); \ if (!(e == CUBLAS_STATUS_SUCCESS)) \ { \ fprintf(stderr, "CUBLAS: %s:%d: error: %d\n", __FILE__, __LINE__, \ e); \ abort(); \ } \ }同上,区别是调用的函数为 CUBLAS 函数。
//column 41 #pragma omp parallel for这是 OpenMP(Opem Multi-Processing)的一个指令,用于并行化一个 for 循环。它告诉编译器在执行这个 for 循环时使用多线程进行计算。其具体作用包括以下方面:
- 并行化for循环: 通常,for循环中的迭代是一个一个按顺序执行的。使用该指令告诉编译器,可以将for循环中的迭代任务分配给多个线程并行执行,从而加速循环的执行。
- 自动线程分配: OpenMP会自动确定并行化的线程数量,以充分利用计算机的多核处理器。这样,程序员无需显式指定线程数量,而是由OpenMP运行时系统自动管理。
- 线程同步: OpenMP会在for循环结束时自动同步线程,确保在循环执行结束后,程序的其他部分能够正常运行而不会发生数据竞争等问题。
dim3 grid((size + block_size - 1) / block_size, (size + block_size - 1) / block_size); dim3 block(block_size, block_size);这两句话将 grid 和 block 定义为了 cuda 中的 dim3 变量。不过只有前两维的变量被使用。
