基本情况
ABC秒了。
DE都给了我希望,但都做不下去。
两道题反复横跳,结果最后谁也没做出来。
E还是比D亲切的,先补E吧。
E. Add Modulo 10
做的时候想着说对每个个位数的变化找找规律,但是没有进一步的发现。
实际上就应该从这里下手。
首先共识:相同的两个数经过操作后必然相同。
分析每一个十进制末位,即数经过一次变换后末位会从啥变成啥:
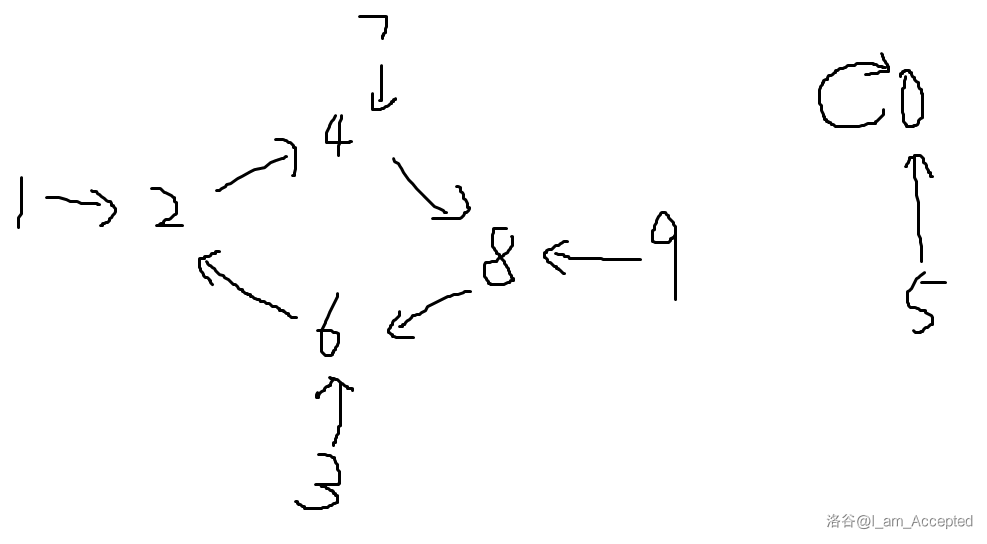
由图得 \(\{a\}\) 中不能同时存在 \(5\) 的倍数和非 \(5\) 的倍数。
若全为 \(5\) 的倍数,将她们的末尾全部操作为 \(0\),判断相等即可。
若全非 \(5\) 的倍数,将她们的末尾全部操作为 \(2\)。由于 \(2\to 4\to 8\to 6\to 2\) 绕一圈后原数会 \(+20\),所以我们判断这些数是否 \(\bmod\ 20\) 同余即可。
#include<iostream>
#include<algorithm>
#include<cstdio>
const int N = 2e5 + 10;
int n, a[N];
void calc(int& x) {while(x % 10 != 2 && x % 10 != 0) x += x % 10;}
void solve()
{
std::cin >> n;
for (int i = 1; i <= n; i++) std::cin >> a[i];
int cnt = 0;
for (int i = 1; i <= n; i++) if (a[i] % 5 == 0) cnt++;
if (cnt > 0 && cnt < n) {std::cout << "NO\n"; return ;}
for (int i = 1; i <= n; i++) calc(a[i]);
if(!cnt) for (int i = 1; i <= n; i++) a[i] %= 20;
for (int i = 2; i <= n; i++) if(a[i] != a[i - 1]) {std::cout << "NO\n"; return ;}
std::cout << "YES\n";
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int _; std::cin >> _;
while(_--)solve();
return 0;
}
D. Color with Occurrences
做的时候真的毫无想法。
没想到居然是DP,想必我知道了是DP也做不出来的。
由于同一段可以被染色多次,所以最小代价和顺序无关。
可以想到动态规划,设 \(dp[i]\) 为将 \(t\) 的前 \(i\) 个字符都染色的最小代价。
考虑如何进行转移,不妨预处理出 \(len_j\) 表示 \(s_j\) 的长度, \(match[i][j]\) 表示 \(s_j\) 能否匹配字符串 \(t\) 中以位置 \(i\) 结尾,长度为 \(len_{j}\) 的子串。这样就很好转移,对于每个位置 \(i\),考虑每个能够匹配的 \(s_j\),对于每个 \(s_j\),从 \([i-len_j,i]\) 区间内转移。注意:由于染色区间可以不交,所以左端点为 \(i-len_j\) 而不是 \(i-len_j+1\)。由此得到状态转移方程如下:
\[dp[i]=\min_{match[i][j]=1} \{\min_{k=i-len_j}^i dp[k]+1\} \]在转移的同时记录 \(from[i]\) 和 \(type[i]\) 数组,记录转移到 \(i\) 的状态的染色终点(即方程中的 \(k\))和染色时使用的模板串编号(即方程中的 \(j\))。
注意 \(dp\) 数组初值应为正无穷,若转移完后 \(dp[n]=\infty\),则报告无解,否则使用记录的 \(from[i]\) 和 \(type[i]\) 递归输出方案即可。单组数据时间复杂度 \(\mathcal O(|t|\sum|s_i|)\),可以通过。参考代码如下:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
const int N = 110;
int dp[N], from[N], ok[N][N];
int len[N], type[N];
std::string s;
void print(int n)
{
if (n == 0) return;
print(from[n]);
std::cout << type[n] << " " << n - len[type[n]] + 1 << std::endl;
return ;
}
void init()
{
std::cin >> s;
memset(dp, 0x3f, sizeof(dp));
memset(from, 0, sizeof(from));
memset(ok, 0, sizeof(ok));
dp[0] = 0;
}
void solve()
{
init();
int n = s.length(), m;
std::cin >> m;
s='0'+s;
for (int i = 1; i <= m; i++)
{
std::string temp; std::cin >> temp; len[i] = temp.length();
for (int j = len[i]; j <= n; j++)
{
if (s.substr(j - len[i] + 1, len[i]) == temp) ok[j][i] = 1;
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
if (!ok[i][j]) continue;
for (int k = i - len[j]; k < i; k++)
{
if (dp[k] + 1 < dp[i])
{
from[i] = k, type[i] = j;
dp[i] = dp[k] + 1;
}
}
}
}
if (dp[n] == 0x3f3f3f3f) std::cout << -1 << std::endl;
else std::cout << dp[n] << std::endl, print(n);
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int _; std::cin >> _;
while(_--) solve();
return 0;
}