CF1474F

传送门

description

用一下方式生成一个序列：

初始序列里有一个数，是什么无所谓。给定 \(n\) 个整数，对第 \(i\) 个整数 \(d_i\)，若 \(d_i\ge 0\)，重复 \(d_i\) 次加入一个值比序列里最后一个值大 1 的数；若 \(d_i<0\)，重复 \(-d_i\) 次加入一个值比序列里最后一个值小 1 的数。

求该序列的最长上升子序列和最长上升子序列（下称 LIS）个数。

• \(n\leq 50\)

• \(|d_i|\leq 10^9\)

hints

solution

如果生成的序列是单调不降的，答案为 \((1,L)\)，其中 \(L\) 是序列长度。

我们先判掉这种情况，下面讨论的都是 \(d_i\) 中至少有一个正数的情况。

先想第一问。

根据题意，生成的序列大概长这样：（每段线段斜率的绝对值都是 1）。

可以观察出以下性质：

• 每个位置结尾的 LIS 的长度是当前位置的值减去它前面（包含）的最小值 +1。

我们顺便可以找到更简单的 LIS 的 dp 的方式：

利用上面的性质就可以免去记录每个位置的 LIS 长度，转移的时候限制第 \(i\) 个位置从 \([lst_i,i-1]\) 中小于它的的位置转移，其中 \(lst_i\) 是 \(i\) 前面的最小值。

这样的 dp 方式还有转移上的性质：

• 转移点的值一定是当前位置的值 -1。否则答案一定不是最优的

这样我们得到了一个按值域从小到大的 dp 方式，对值域里的每个数转移的计算量是 \(O(n^2)\) 的。

这样就有了 \(O(n^2V)\) 的做法，不能接受。

不过我们感觉这个序列有某些连续的段中的位置性质比较相似。思考一下可以试试这样给原序列在值域上分个层：

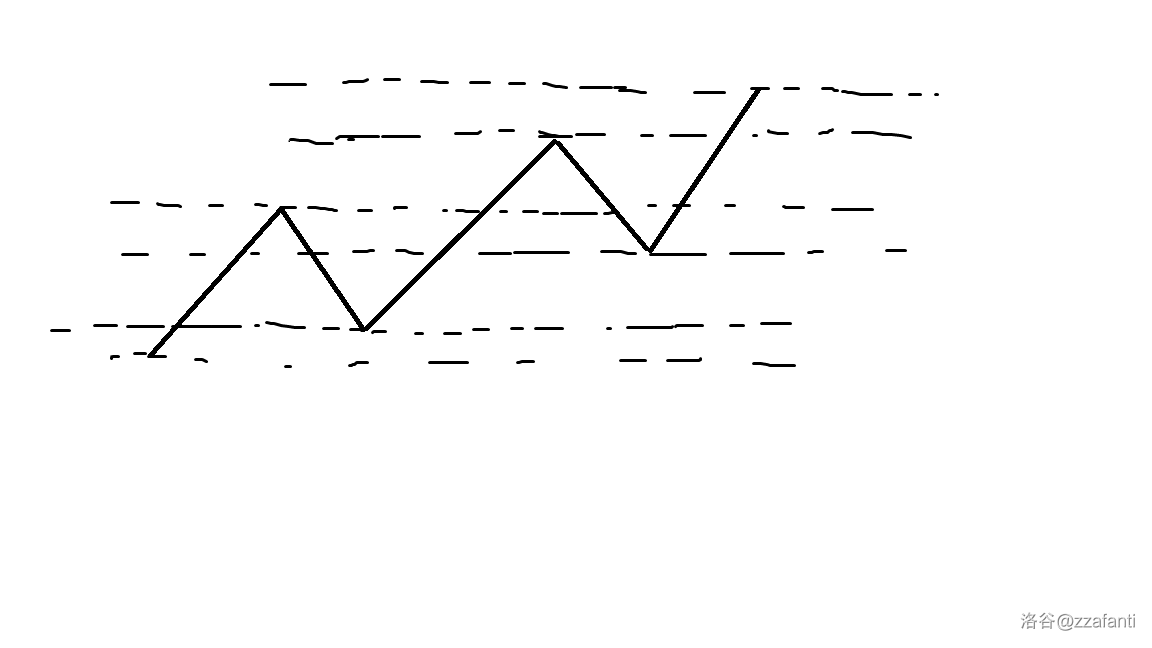
就是在每个拐点的纵坐标构成的集合划分割线。这样我们把原序列在值域上分成了大约 \(n\) 层。答案只可能在每层的上边界处被更新。

有没有发现每层内值域上每个数的转移似乎是一样的啊。

把转移塞到矩阵里，矩阵快速幂就做完了，\(O(n^4\log V)\)

实现上需要注意点细节：

原序列可以看成二维平面上横坐标为连续正整数的离散的点构成的集合，但是我们上面认为它是直线，实际处理的时候要注意拐点处的边界情况。

分层之后还需要注意怎么赋初值和更新答案，每层 dp 跑前跑后扫一扫统计一下就好。

具体地，拐点包含在两条上面画的折线段中，上凸的拐点处是要统计答案的位置；下凸的拐点处要赋初值，如果它是前缀最小值，那么初值赋 1，这里我把它赋给了右边（也就是递增的那个线段），因为左边递减的线段一定不会对答案产生影响。如果它不是前缀最小值，像普通的点一样转移出来初值就行了。

code

Submission #236338536 - Codeforces