Generative-Contrastive Graph Learning for Recommendation论文阅读笔记

Abstract

首先介绍了一下GCL的一些缺点，GCL是通过数据增强来构造对比视图，然后通过最大化对比视图之间的互信息来提供自监督信号。但是目前的数据增强技术都有着一定的缺点

• 结构增强随机退出节点或边，容易破坏用户项目的内在本质
• 特征增强对每个节点施加相同的尺度噪声增强，忽略的节点的独特特征
  所以这篇论文的主要创新贡献点就在改变GCL的数据增强方面，采用了变分图自编码器来进行数据增强
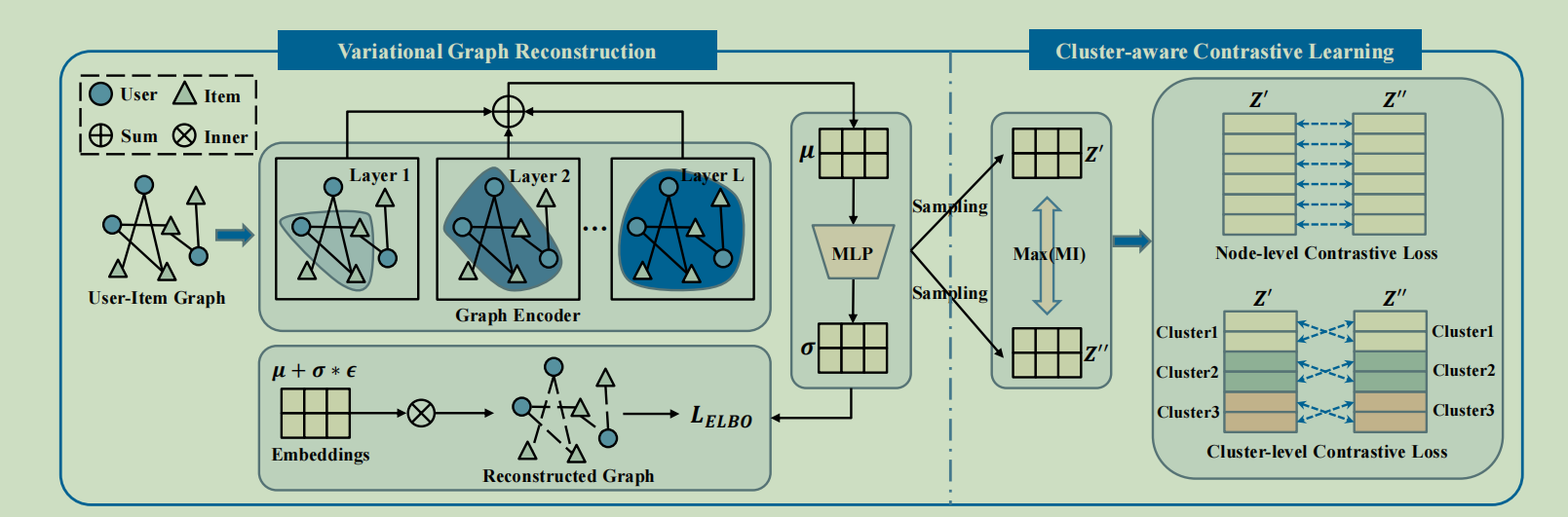
  为了解决上面的缺点，提出了一个新的变分图生成-对比学习（VGCL）框架的推荐，具体来说，就是利用变分图重建来估计每个节点的高斯分布，然后通过对估计分布的多个抽样，生成多个对比视图，生成的对比视图可以很好的重建输入图而不产生信息失真。考虑到估计分布的相似性，我们提出了一种集群感知的双重对比学习，节点级鼓励节点的对比视图的一致性，集群级鼓励集群中节点的一致性。

Introduction

基于图的CF模型在模型学习中存在稀疏监督问题，所以需要引入一种替代方案。自监督学习利用输入数据本身作为监督信号。然后就开始介绍GCL的缺点，数据增强是GCL的关键，但是当前的数据增强方案都有缺陷。所以在本文中，我们利用了生成模型的潜力来促进对比视图的生成，而不需要数据增强。具体来说，我们提出了一个变分图生成-对比学习框架的推荐，通过对估计分布的多个抽样生成多个对比视图，而不是利用数据来增强图。这样就将生成模型和对比模型之间建立起了联系。生成的对比视图可以很好的重建输入图而不产生信息失真。估计的方差也可以针对每个节点进行定制，可以自适应的调节每个节点的对比损失规模将进行优化，然后因为相似的节点在表示空间中更接近，提出了具有两个对比目标的聚类感知对比学习，第一个是节点级的对比损失，鼓励了每个节点的多个视图的一致性。第二种是集群级的对比损失，鼓励了集群中不同节点的一致性，并从节点的估计分布中学习到集群。
这里有点疑问，为啥鼓励集群中不同节点的一致性，以及怎么从节点的估计分布中学习到集群。
本文的主要贡献：

• 从更好的对比视图构建的角度，引入了一种新的生成-对比图学习范式，并提出了新的变分图生成对比学习框架进行推荐
• 利用变分图重建来生成对比视图，并设计了一个集群感知的双重对比学习模块，就可以在不同的尺度上更好的挖掘基于GCL的推荐的自监督信号

Preliminaries

这里介绍一下隐式反馈(implicit feedback)的概念。在推荐系统里，分为隐式数据和显式数据。比如用户对电影的评分，这是显示数据集。隐式数据就是用户的浏览，收藏，购买等行为。
然后介绍一下什么是Readout函数，我们有时候需要整个图的特征表示，但是只有每个节点的特征表示，此时Readout函数通过聚合节点特征的方式来得到整图的特征表示。
GCL通常作为辅助任务，补充自我监督信号，进行多任务学习。
最后简要介绍一下长尾分布，也就是市场中小而散的个性化需求的总和也能产生极为惊人的利益，通俗的说，也就是“小利润，大市场”

Methodology

这个是VGCL的整体的一个架构

变分图重建

图推断

VGCL由两个模块组成，一个变分图重构模块和一个聚类感知的对比学习模块。具体来说，我们首先使用变分图重建来估计每个节点的概率分布，然后设计聚类感知的两个对比学习目标，以鼓励从估计的分布中产生的多个抽样产生的对比视图的一致性。
VAE的部分就不详细介绍了，来介绍一下图推断（Graph Inference）
假设有一个用户-项目交互图\(\mathcal{G}=\{U\cup V,A\}\) ，和初始化的节点嵌入\(E_0\)，图推理的目的是学习概率分布Z，它可以重建输入图的结构 \(\hat{A}\sim p_{\theta}(A|Z)\)。与VAE相似，我们也采用变分推断\(q_{\phi}\{Z|A,E_0\}=\Pi_{i=0}^{M+N-1}q_{\phi}\{z_i|A,E_0\}\)来近似后验概率\(p_{\theta}(A|Z)\) 。具体的说，我们编码每一个节点到一个多元高斯分布\(q_{\phi}\{z_i|A,E_0\}=\mathcal{N}(z_i|\mu_{\phi}(i),diag(\sigma_{\phi}^2(i)))\)，其中\(\mu_{\phi}(i)\) 和\(\sigma_{\phi}^2(i)\)表示节点i分布的均值和方差。为了更好地利用高阶用户-项目图结构，我们采用GNN来估计节点分布的参数
\(\mu=GNN(A,E_0,\phi_{\mu}),\sigma=GNN(A,E_0,\phi_{\sigma})\)，其中\(\phi_{\mu},\phi_{\sigma}\)表示图推理的可学习参数。根据之前对基于图的协同过滤的研究，我们采用LightGCN作为编码器来部署上述图推理。对于每个节点i，评价值的更新过程如下：

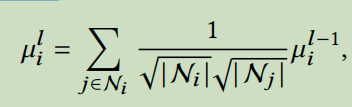
\(\mu_i^l\)和\(\mu_{i}^{l-1}\)是对应第l层和第l-1层的平均值，\(N_i\)和\(N_j\)是节点i和节点j的平均值，我们初始化平均值\(\mu^0=E^0\)，这样我们就可以得到L+1层的平均值输出，然后我们融合所有层的输出并且计算对应的平均值和方差
\(\mu=\frac{1}{L}\sum^{L}_{l=1}\mu^l,\sigma=MLP(\mu)\)
方差是由以平均值为输入的MLP生成的，我们发现单层的MLP达到了最好的表现，于是\(\sigma=exp(\mu W+b)\)，在得到均值和方差后，我们通过采样来生成潜在表示\(z_i\)，但是因为采样过程是不可微的，所以它不能进行定向优化，于是就采用重参数化的技巧：\(z_i=\mu_i+\sigma_i*\varepsilon\)

图生成

在估计了潜在变量Z的概率分布后，生成图的目标是重建原始的用户-项目图
\(p(A|Z)=\Pi_{i=0}^{M+N-1}\Pi_{j=0}^{M+N-1}p(A_{ij}|z_i,z_j)\)
有许多方法来实现图形生成过程，比如内积，因子分解机和神经网络，这里使用内积来计算节点i与节点j连接的倾向得分(个人的一点想法，为什么是用内积，没有说明，用其它的方法效果会不会好一些)
\(p(A_{ij}=1|z_i,z_j)=\sigma(z_i^Tz_j)\)

集群感知的对比学习

对比视图图重建

给出了潜在表示\(z\sim N(\mu,\sigma^2)\)的概率分布，我们引入了一种新的基于估计分布的对比学习范式，我们通过对估计分布的多次抽样来构建对比视图，而不是进行数据增强。对每个节点i，我们生成对比表示\(z_i'\)和\(z_i''\) 。
然后开始介绍这样做的优点，首先从估计的分布中采样，可以很好的重构输入图，其次将估计的方差对每个节点进行量身定制，可以自适应的调节对比损失的规模（这里怀疑一下，为什么可以调节）

节点级别的对比损失

在构建每个节点的对比视图后，我们最大化互信息，提供自监督信号以提高推荐性能。考虑到相似的节点在表示中更接近，我们提出了集群感知的两个优化对比目标，节点级对比损失和集群级对比损失，其中节点级对比损失促进了每个节点的对比视图的一致性，集群级对比损失促进了集群中节点的对比视图的一致性
节点级对比学习的目标函数是\(L_N=L_N^U+L_N^V\) ，分别代表了用户侧损失和项目侧损失。\(B_u,B_i\)表示batch训练数据里面的用户和项目

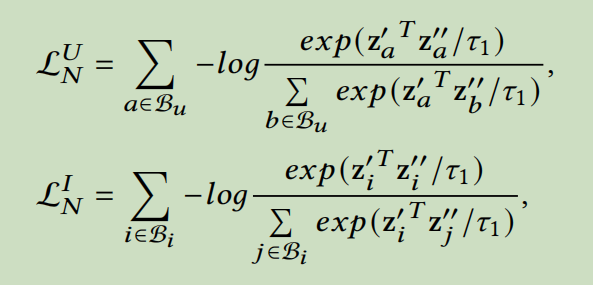
集群级对比损失

设计这个是为了进一步区分批量训练数据中的正、负比对。目标是最大化具有相同集群的节点对的一致性，并最小化具有不同集群的节点对的一致性
假设有\(K_u\)个用户原型\(C_u\)以及\(K_i\)个项目集群原型\(C_i\)，我们使用\(p(c_k^u|z_a)\)来表示用户a属于第k个用户集群的概率。给定估计的分布作为输入，我们采用K-Means算法实现了聚类过程，然后计算两个用户（项目）被分配给同一个原型的概率。（个人的一些想法，这篇文章使用的聚类方法真的好吗，可不可以采用其它的聚类方法，或者直接替换掉集群级对比损失变成其它方法呢）

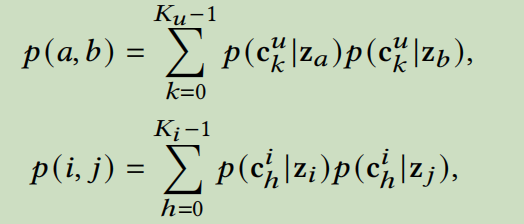
p(a,b)表示用户a和用户b被分配给同一个原型的概率。p(i,j)表示项目i和项目j属于同一个集群的概率。
然后这里定义了集群级别的对比损失\(L_C=L_C^U+L_C^I\)

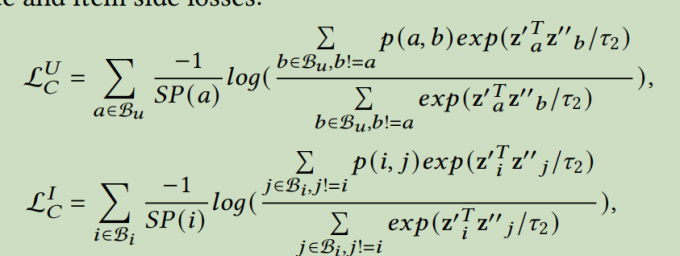
其中SP(a)=\(\sum_{b\in B_u,b!=a}p(a,b)\)
（个人不是很理解加上这个SP是为了什么）
最终的对比损失是节点级损失和集群级损失的加权和
\(L_{cl}=L_N+\gamma L_C\)

模型优化

对于变分图重建部分，我们使用ELBO优化图推理和图生成的参数
最后我们提出的VGCL的优化函数为
\(minL=L_{ELBO}+\alpha L_{cl}+\lambda||E^0||^2\)
模型的最终算法如下：

Conclusion

在本篇文章中，我们从更好的对比视图构建的角度研究了基于GCL的推荐，并且提出了一个新的变分图生成-对比学习框架。利用变分图重建技术而不是数据增强来生成对比视图。具体来说，就是先通过图的变分推理来估计每个节点的概率分布，然后从估计的分布中生成具有多个抽样的对比视图。这个方法的优点有两个方面。首先，生成的对比表示可以很好的重建原始图而不产生信息失真。其次，估计的方差来自不同的节点，这可以自适应的条件每个节点的对比损失的规模。然后提出了集群感知的双重对比学习，节点级鼓励节点对比视图的一致性，集群级鼓励集群中节点的一致性。