FPN特征金字塔

FPN特征金字塔

论文地址 https://arxiv.org/pdf/1612.03144.pdf

目标的多尺度一直是目标检测算法极为棘手的问题。像Fast R-CNN，YOLO这些只是利用深层网络进行检测的算法，是很难把小目标物体检测好的。因为小目标物体本身的像素就比较少，随着降采样的累积，它的特征更容易被丢失。为了解决多尺度检测的问题，传统的方法是使用图像金字塔进行数据扩充。虽然图像金字塔可以一定程度解决小尺度目标检测的问题，但是它最大的问题是带来计算量的极大的增加，而且还有很多冗余的计算。

低层的特征语义信息比较少，但是目标位置准确；高层的特征语义信息比较丰富，但是目标位置比较粗略。利用浅层的特征就可以将简单的目标的区分开来；利用深层的特征可以将复杂的目标区分开来

提出了 FPN 结构如下图：这个金字塔结构包括一个自底向上的线路，一个自顶向下的线路和横向连接（lateral connections）。

背景知识

在FPN之前，目标检测不同的卷积结构类型

图（a）特征图像金字塔，它通过将输入图像缩放到不同尺度的大小构成了图像金字塔。然后将这些不同尺度的特征输入到网络中（可以共享参数也可以独立参数），得到每个尺度的检测结果，然后通过NMS等后处理手段进行预测结果的处理。

对每一种尺度的图像进行特征提取，能够产生多尺度的特征表示，并且所有等级的特征图都具有较强的语义信息。
推理时间大幅度增加；
内存占用巨大，端到端训练比较麻烦

图（b）利用单个高层特征图进行预测。浅层的网络更关注于细节和位置信息，高层的网络更关注于语义信息，而高层的语义信息能够帮助我们准确的检测出目标，因此我们可以利用最后一个卷积层上的feature map来进行预测。

是Fast R-CNN ，Faster R-CNN，YOLO等算法的网络结构，它只使用卷积网络的最后一层作为输出层。
主要问题就是对小尺寸的目标检测效果非常不理想。因为小尺寸目标的特征会随着逐层的降采样快速损失，到最后一层已经有很少的特征支持小目标的精准检测。

图（c）同时利用低层特征和高层特征，分别在不同的层同时进行预测

对于简单目标，我们视同低层特征，对于复杂目标，我们利用复杂特征。
是SSD采用的结构，它首先提出了使用不同层的Feature Map进行检测的思想。对于简单的目标我们仅仅需要浅层的特征就可以检测到它，对于复杂的目标我们就需要利用复杂的特征来检测它。
SSD只是单纯的从每一层导出一个预测结果，没有进行特征融合。
没有特征融合和特征复用，没有给高层特征赋予浅层特征擅长检测小目标的能力，也没有给浅层的特征赋予高层捕捉到的语义信息，提升结果有限。

图（d）（FPN网络）

首先我们在输入的图像上进行深度卷积，然后对Layer2上面的特征进行降维操作（即添加一层1x1的卷积层），对Layer4上面的特征就行上采样操作，使得它们具有相应的尺寸，然后对处理后的Layer2和处理后的Layer4执行加法操作（对应元素相加），将获得的结果输入到Layer5中去。其背后的思路是为了获得一个强语义信息，这样可以提高检测性能。其实看下面的代码就可以明白，把卷积之后的{Ck}层和上采样之后的{Pk}层进行相加，目的是把低层次高分辨率的信息和高层次强语义的信息结合起来，提高检测性能和小目标识别。

FPN网络结构

通过 ResNet50 网络，通过自底向上路径，FPN得到了四组Feature Map，最后利用 C2，C3，C4，C5 建立特征图金字塔结构：

为了将这四组倾向不同特征的Feature Map组合起来，FPN使用了自顶向下及横向连接的策略，最终得到P2，P3，P4，P5四个输出。

1、将 C5 经过 256 个 1x1 的卷积核操作得到：32x32x256，记为 P5；

2、将 P5 进行步长为 2 的上采样得到 64x64x256，再与 C4 经过的 256 个 1x1 卷积核操作得到的结果相加，得到 64x64x256，记为 P4；

3、将 P4 进行步长为 2 的上采样得到 128x128x256，再与 C3 经过的 256 个 1x1 卷积核操作得到的结果相加，得到 128x128x256，记为 P3；

4、将 P3 进行步长为 2 的上采样得到 256x256x256，再与 C2 经过的 256 个 1x1 卷积核操作得到的结果相加，得到 256x256x256，记为 P2；

结合从 P2 到 P5 特征图的大小，如果原图大小 1024x1024, 那各个特征图对应到原图的步长依次为 [P2,P3,P4,P5,P6]=>[4,8,16,32]。

5、FPN 在 P2，P3，P4，P5 之后均接了一个 3×3 卷积操作，该卷积操作是为了减轻上采样的混叠效应（aliasing effect）。

FPN结构特点

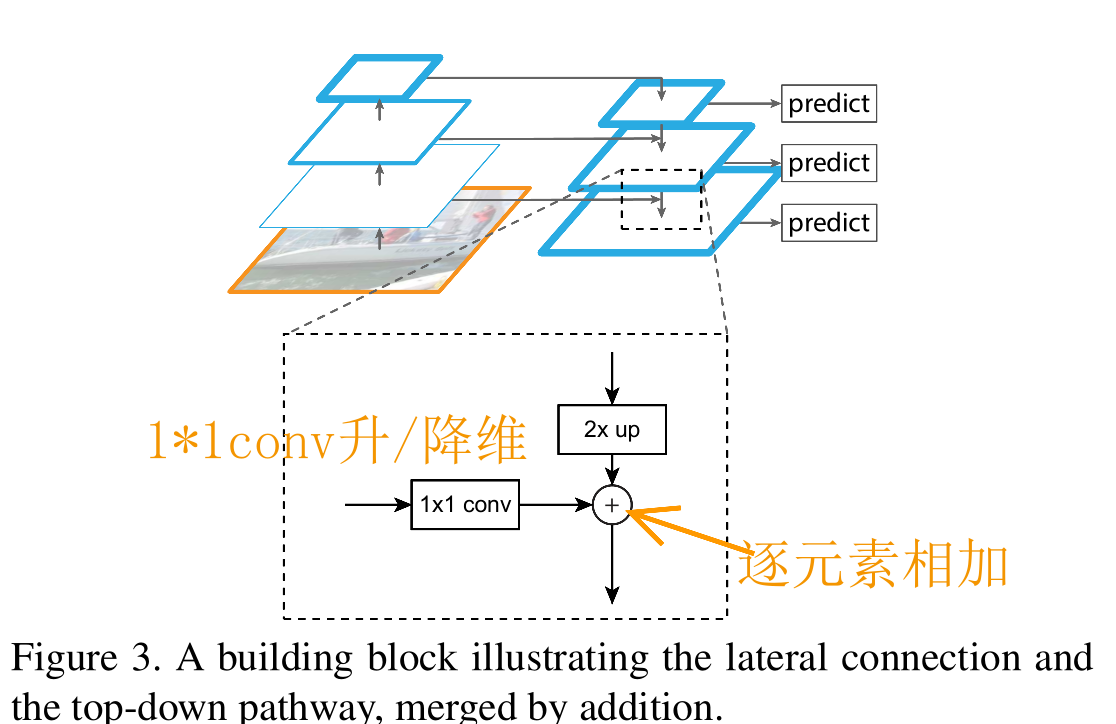
自下而上: 最左侧为backbone，默认使用ResNet结构,每一级往上用 step=2 的降采样

自上而下: 首先对C5进行1×1卷积降低通道数得到P5，然后依次进行上采样（最近邻插值）得到P4、P3和P2，目的是得到与C4、C3与C2长宽相同的特征，以便进行逐元素相加。

横向连接: 将上采样后的高语义特征与浅层的定位细节特征进行融合，采用1×1卷积使其通道数变为256，解决维度不一致问题，然后元素相加。

卷积融合: 在得到相加后的特征后，利用3×3卷积对生成的P2至P4再进行融合，目的是消除上采样过程带来的重叠效应，以生成最终的特征图。

结构总结

FPN是最早在目标检测方向上提出特征融合的算法，开辟了特征融合的先河，为之后PANet，NAS-FPN等算法的提出打下了基础。

FPN是一个特征金字塔的结构。FPN的这种特征金字塔的结构是非常符合CNN的结构特征的，通过将深层语义信息和浅层纹理信息进行融合，为每一层的Feature Map都赋予了更强的捕捉语义信息的能力。

FPN能够很好地处理小目标的主要原因是：

FPN可以利用经过top-down模型后的那些上下文信息（高层语义信息）；
对于小目标而言，FPN增加了特征映射的分辨率（即在更大的feature map上面进行操作，这样可以获得更多关于小目标的有用信息）

代码实现

lass FPN(nn.Module):
    def __init__(self, block, layers):
        super(FPN, self).__init__()
        self.inplanes = 64

        self.conv1 = nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3, bias=False)
        self.bn1 = nn.BatchNorm2d(64)

        self.relu = nn.ReLU(inplace=True)
        self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
        # Bottom-up layers
        self.layer1 = self._make_layer(block,  64, layers[0])
        self.layer2 = self._make_layer(block, 128, layers[1], stride=2)
        self.layer3 = self._make_layer(block, 256, layers[2], stride=2)
        self.layer4 = self._make_layer(block, 512, layers[3], stride=2)

        # Top layer
        self.toplayer = nn.Conv2d(2048, 256, kernel_size=1, stride=1, padding=0)  # Reduce channels

        # Smooth layers
        self.smooth1 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)
        self.smooth2 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)
        self.smooth3 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)

        # Lateral layers
        self.latlayer1 = nn.Conv2d(1024, 256, kernel_size=1, stride=1, padding=0)
        self.latlayer2 = nn.Conv2d( 512, 256, kernel_size=1, stride=1, padding=0)
        self.latlayer3 = nn.Conv2d( 256, 256, kernel_size=1, stride=1, padding=0)
        
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
                m.weight.data.normal_(0, math.sqrt(2. / n))
            elif isinstance(m, nn.BatchNorm2d):
                m.weight.data.fill_(1)
                m.bias.data.zero_()

    def _make_layer(self, block, planes, blocks, stride=1):
        downsample  = None
        if stride != 1 or self.inplanes != block.expansion * planes:
            downsample  = nn.Sequential(
                nn.Conv2d(self.inplanes, block.expansion * planes, kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(block.expansion * planes)
            )
        layers = []
        layers.append(block(self.inplanes, planes, stride, downsample))
        self.inplanes = planes * block.expansion
        for i in range(1, blocks):
            layers.append(block(self.inplanes, planes))

        return nn.Sequential(*layers)


    def _upsample_add(self, x, y):
        _,_,H,W = y.size()
        return F.upsample(x, size=(H,W), mode='bilinear') + y

    def forward(self, x):
        # Bottom-up
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.relu(x)
        c1 = self.maxpool(x)
        
        c2 = self.layer1(c1)
        c3 = self.layer2(c2)
        c4 = self.layer3(c3)
        c5 = self.layer4(c4)
        # Top-down
        p5 = self.toplayer(c5)
        p4 = self._upsample_add(p5, self.latlayer1(c4))
        p3 = self._upsample_add(p4, self.latlayer2(c3))
        p2 = self._upsample_add(p3, self.latlayer3(c2))
        # Smooth
        p4 = self.smooth1(p4)
        p3 = self.smooth2(p3)
        p2 = self.smooth3(p2)
        return p2, p3, p4, p5

参考资料

https://zhuanlan.zhihu.com/p/460738972 详细

https://zhuanlan.zhihu.com/p/125749758

https://zhuanlan.zhihu.com/p/397293649

标签：nn,特征,self,FPN,stride,金字塔,256
From： https://www.cnblogs.com/tian777/p/17864990.html

FPN特征金字塔