有点意思的简单题。
答案有可二分性。合并两段,显然仍然合法。
考虑如何 check。因为答案可以被二分,我们尝试求恰好 \(x\) 段就行了。
恰好,这是 wqs 二分的内容。如何设计一个与 \(x\) 有关的凸函数呢?
这个函数大概是 \(\sum_{i=1}^x w(l_i, r_i)\) 的形式,每一个 \([l, r]\) 都是合法的一段,且互相不重叠。这样就能记录段数了,也就可以为每一段附加权值了。
假如分成了 \(x\) 段,只需要这 \(x\) 段的长度和 \(\leq n-(k-x)\) 就行了。但是这样不行,因为右侧与 \(x\) 有关,这样需要对每个 \(x\) 求值。移项,变成每一段的长度减去一不超过 \(n-k\),这就把状态变成了 \(O(n)\) 个。
因此 \(w(l, r) = r - l\),合法等价于 \(\sum w(l, r) \leq n-k\),要求每一段 \([l, r]\) 都合法。
设 \(f(x)\) 为:划分出 \(x\) 个合法段 \([l_i, r_i]\),\(w(l_i, r_i)\) 之和。下面搬运官方题解对这个函数具有凸性的证明。(它是一个下凸壳,因为取一段的代价是越来越高的。)
假设 \(B_1 \sim B_m\) 是 \(m\) 个极短合法段。因为极短,两两不具有包含关系。因此我们假定这 \(m\) 段右端点、左端点均递增。
设 \(f(p)\) 对应的方案的极短合法段的编号是 \(x_1 \sim x_{p}\),\(f(p+2)\) 对应的方案的极短合法段的编号是 \(y_1 \sim y_{p+2}\)。先延长每一段左端点让它们两两相接,假设没有一个 \(y\) 被完整包含到 \(x\) 中,\(y\) 最多只能有 \(p+1\) 个,矛盾。因此设 \(y_{i+1}\) 被包含于 \(x_i\) 中,取 \(x_1 \sim x_{i-1}, y_{i+1} \sim y_{p+2}\) 和 \(x_1 \sim y_i, x_i \sim x_{p}\) 构成两个长度为 \(p+1\) 的合法解,因此有 \(2f(p+1) \leq f(p) + f(p+2)\),凸性得证。
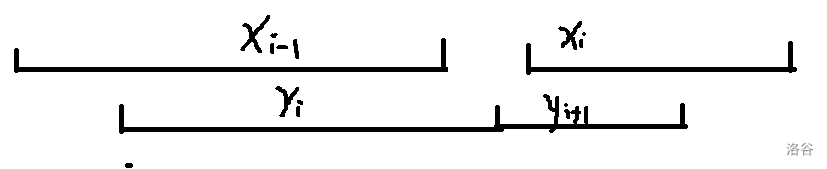
(延长左端点前的图,可以证明延长后存在一个 \(y_{i}\) 被包含于 \(x_i\) 中,\(y_i\) 与 \(y_{i+1}\) 不一定相接,但这不影响。)
因此,我们得到了一个 \(O(n \log^2 n)\) 的做法,代码。
- 二分是否分为恰好 \(x\) 段是可以的。注意这里的上界是 \(k\)。
- 设 \(f(x)\) 为:分成恰好 \(x\) 段的 \(\sum w(l, r)\) 的最小值。这是一个下凸壳,因此对其进行 wqs 二分找到 \(f(x)\)。如果这个最小值不超过 \(n-k\) 就认为可以分成 \(x\) 段。
对于 \((x, f(x))\) 组成的下凸壳,第二个二分对其单点求值。但是,因为我们只能用一条斜线切凸包并得到切到的点的坐标,在求一个点的坐标时获得了额外的其它点的坐标。能不能只做一次二分呢?
注意到我们需要的是 \(y\) 坐标不超过 \(n-k\) 的点的横坐标的最大值,当切线的斜率单调变化时,切到的点是否合法也是单调的,因此直接二分切线的斜率就够了。
因此我们得到了一个 \(O(n \log n)\) 做法,代码(官方代码)。
标签:二分,极短,Subsegments,Sums,合法,Large,端点,一段,sim From: https://www.cnblogs.com/purplevine/p/solution-arc168e.html