计算几何

Link

UVA 11178 Morley's Theorem

Question

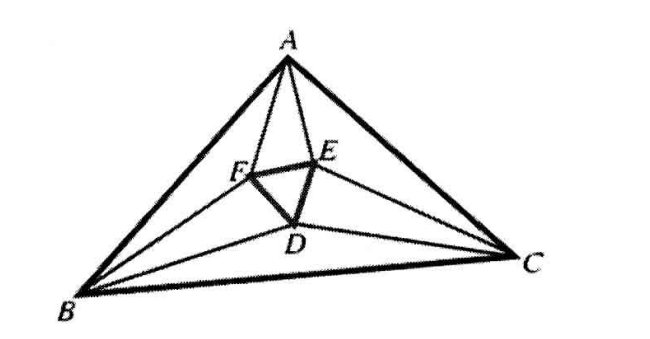
Morley 定理是这样的，作三角形 ABC 每个内角的三等分线，相交成三角形 DEF，则 DEF 是等边三角形

给出 \(A,B,C\) 坐标，求 \(D,E,F\) 坐标

Solution

其实是一道计算几何板子题只需要计算 \(\angle ABC\) 的值 \(a\)，然后把 \(BC\) 逆时针旋转 \(a/3\) 就能得到 \(BD\) 同理能得到直线 \(CD\) 就能求得交点 \(D\)

Code

#include<bits/stdc++.h>
using namespace std;

struct Point{
    double x,y;
    Point(double x=0,double y=0):x(x),y(y){};
};
typedef Point Vector;

Vector read_point(){
    Point ret;
    cin>>ret.x>>ret.y;
    return ret;
}

Vector operator + (Vector A,Vector B) {return Vector{A.x+B.x,A.y+B.y};} //向量+向量=向量
Vector operator - (Point A,Point B) {return Vector{A.x-B.x,A.y-B.y};} //点-点=向量
Vector operator * (Vector A,double p) {return Vector{A.x*p,A.y*p};} //向量*数=向量
Vector operator / (Vector A,double p) {return Vector{A.x/p,A.y/p};} //向量/数=向量


const double eps=1e-9;
int dcmp(double x){if(fabs(x)<eps) return 0;else return x<0?-1:1;}
bool operator ==(const Point &a,const Point &b){
    return dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0;
}

double Dot(Vector A,Vector B) {return A.x*B.x+A.y*B.y;}
double Length(Vector A) {return sqrt(Dot(A,A));}
double Angle(Vector A,Vector B) {return acos(Dot(A,B)/Length(A)/Length(B));}
double Cross(Vector A,Vector B) {return A.x*B.y-A.y*B.x;}

//向量逆时针旋转 rad
Vector Rotate(Vector A,double rad){return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));} //rad是弧度

//求两条直线的交点
Point GetLineInersection(Point P,Vector v,Point Q,Vector w){
    Vector u=P-Q;
    double t=Cross(w,u)/Cross(v,w);
    return P+v*t;
}


Point getD(Point A,Point B,Point C){
    Vector v1=C-B;
    double a1=Angle(A-B,v1);
    v1=Rotate(v1,a1/3);
    
    Vector v2=B-C;
    double a2=Angle(A-C,v2);
    v2=Rotate(v2,-a2/3);

    return GetLineInersection(B,v1,C,v2);
}

int main(){
    // freopen("11178.in","r",stdin);
    // freopen("11178.out","w",stdout);
    Point A,B,C,D,E,F;
    int T;
    scanf("%d",&T);
    while(T--){
        A=read_point();
        B=read_point();
        C=read_point();
        D=getD(A,B,C);
        E=getD(B,C,A);
        F=getD(C,A,B);

        printf("%.6lf %.6lf %.6lf %.6lf %.6lf %.6lf\n",D.x,D.y,E.x,E.y,F.x,F.y);
    }
    return 0;
}