首页 > 其他分享 >锦城 Week0 Blog 对拍 Debug 复杂度

锦城 Week0 Blog 对拍 Debug 复杂度

时间：2023-11-14 11:24:20浏览次数：28  
标签：std int 复杂度 Blog cpp Debug Week0 include 我们

Blog

我们在学习的时候，需要些一些笔记，把所学记录和整理下来，作为计算机专业的学生，不太可能用纸笔来记笔记，所以我们需要写博客(Blog)

众多大佬都有自己的博客

美团技术团队

Martian148的博客

写博客可以帮助我们更好的吸收，消化知识，把自己所学的东西用简单的话语讲出来(费曼学习法) 并且，方便查找，复习

作为博客可以写的东西很多，技术的文章，非技术的随想等等

就算法学习而言，我们的博客需要包括以下几个部分

  • 算法学习笔记
    image.png
  • 题解
    image.png
    现在，开始从零开始写博客

首先，创建一个自己博客，创建博客的方式有很多

  • 洛谷博客
  • 博客园/CSDN/知乎
  • GitHub静态部署
  • 租服务器+框架/手写

难度由高到低，喜欢折腾的或者有前端基础的可以去试试后面两项，搭建和维护需要花费的时间比较多

接下来，以洛谷博客为例

打开洛谷博客后台管理网站

文章->新建文章

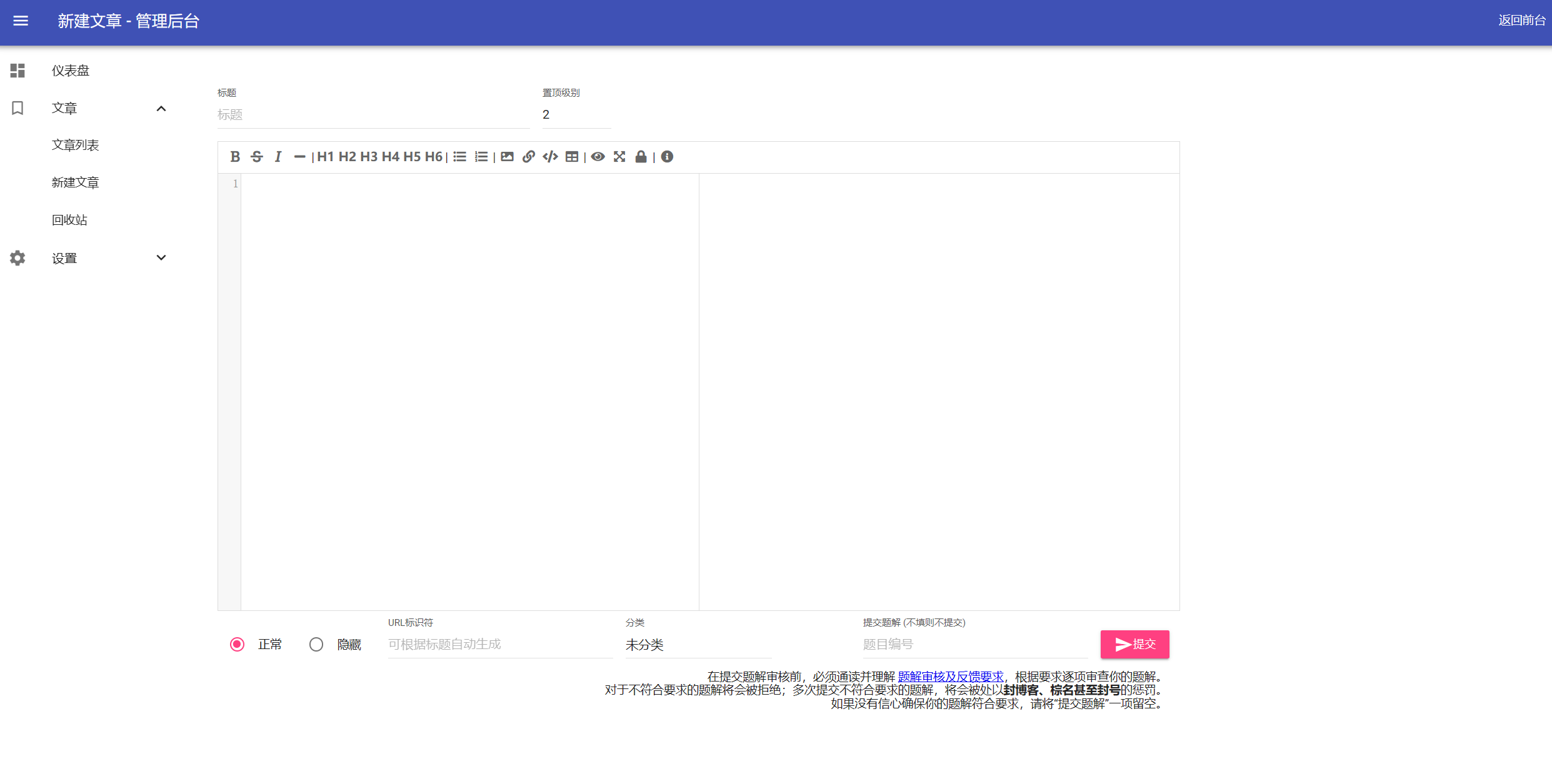
image.png

按照页面上的提示，写下内容

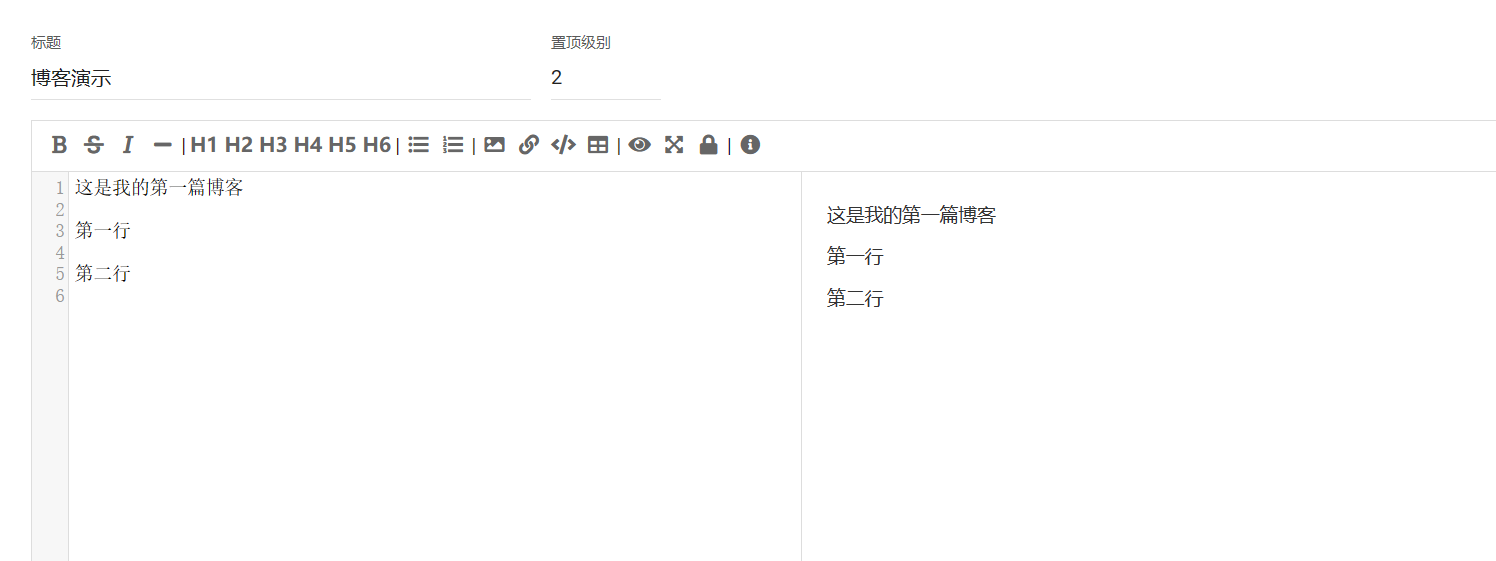
image.png

我们在左边书写内容的时候，会自动同步到右边

可以理解为，左边是书写去，右边是阅读区，因为我们博客的内容可能不止文字，还包括图片，代码，链接，等等

Markdown

Markdown语言不是一种编程语言，可以把他理解成一种标记语言，他用非常简单的语法告诉浏览器如何渲染文章

Markdown语言基础语法：

  • 换行需要两个换行(有些博客平台可能不同)

例如上面的例子

  • 标题

Markdown有 6 级标题，用 # 表示， # 的个数越少，标题级数越高

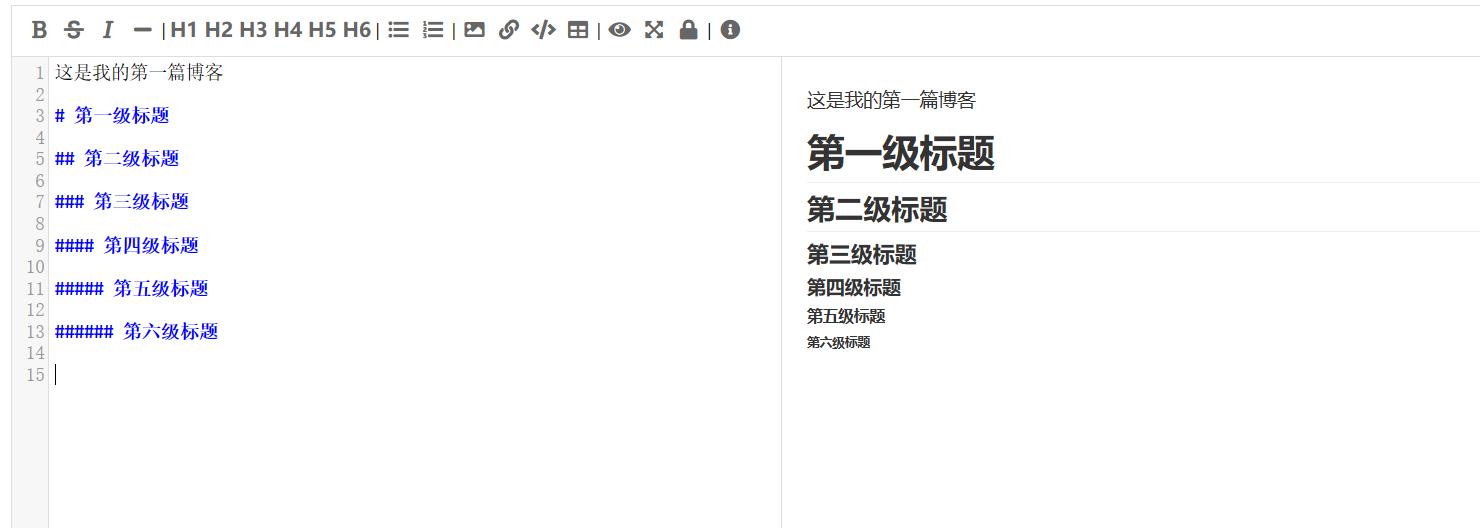
image.png

字体大小从大到小，但是不建议用 # 来控制字体大小

  • 加粗

在字两边加 *

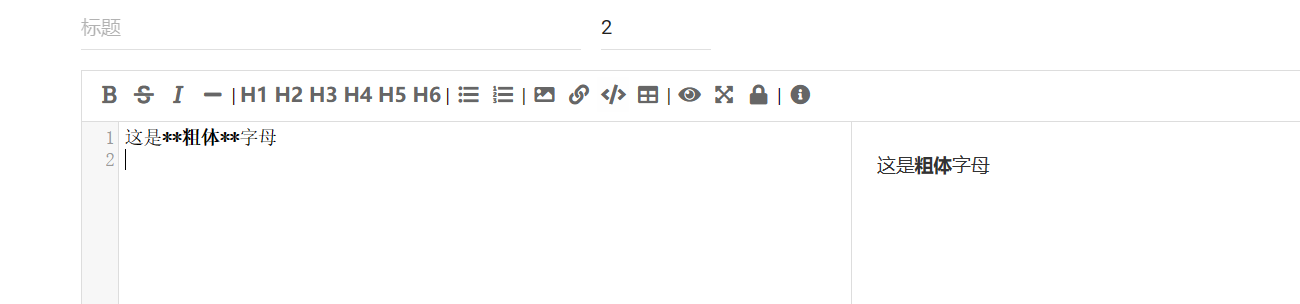
image.png

  • 插入代码

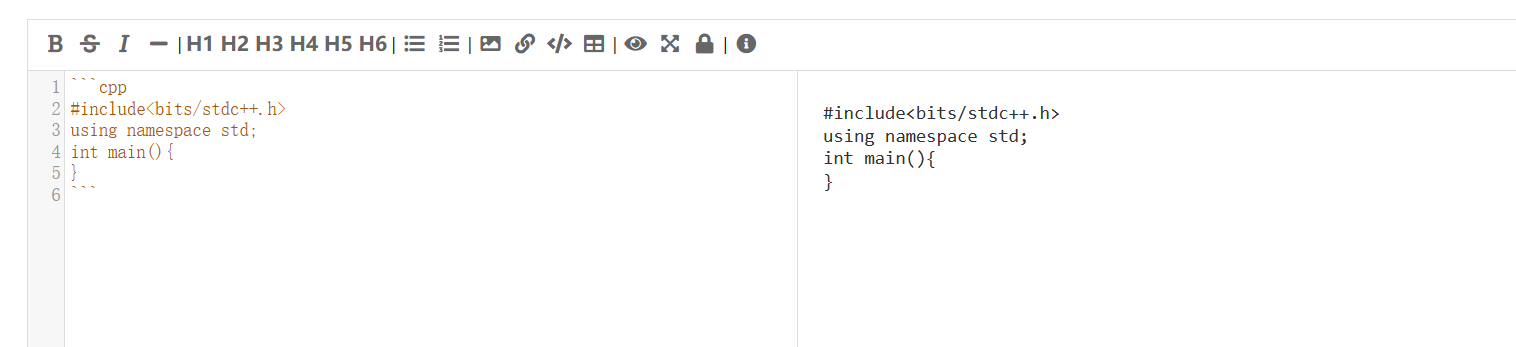
image.png

如果不写 C++ 写别的语言把 cpp 改成别的，比如 java，python

浏览器会根据语言来渲染出色彩

image.png

  • 插入图片

我们使用 ![图片名字](图片链接) 的格式来插入图片

图片名字可以不写(不建议)

那么图片链接是什么呢，可以是本地的图片，但是我们要将文章发布到网上时，无法访问本地的图片，需要把图片也一起传到网上，这个时候就需要图床帮忙了

常见的图床有很多

  • sm.ms
  • 路过图床
  • 洛谷图床(有水印)

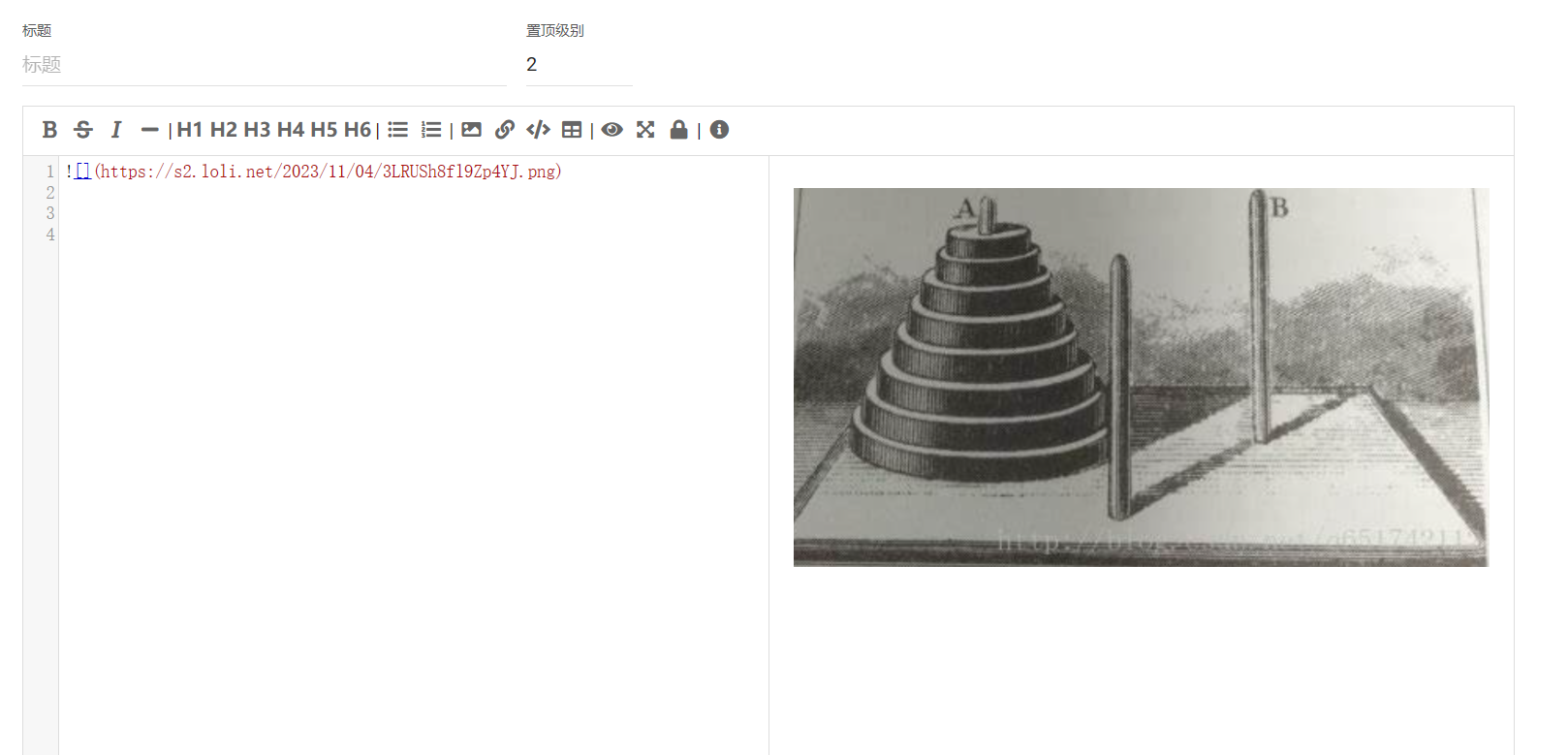
打开[sm.ms] (https://sm.ms/)

image.png

登录后，点击上传，选中本地的一个图片

image.png

上传成功后，需要得到图片的URL也就是图片的链接

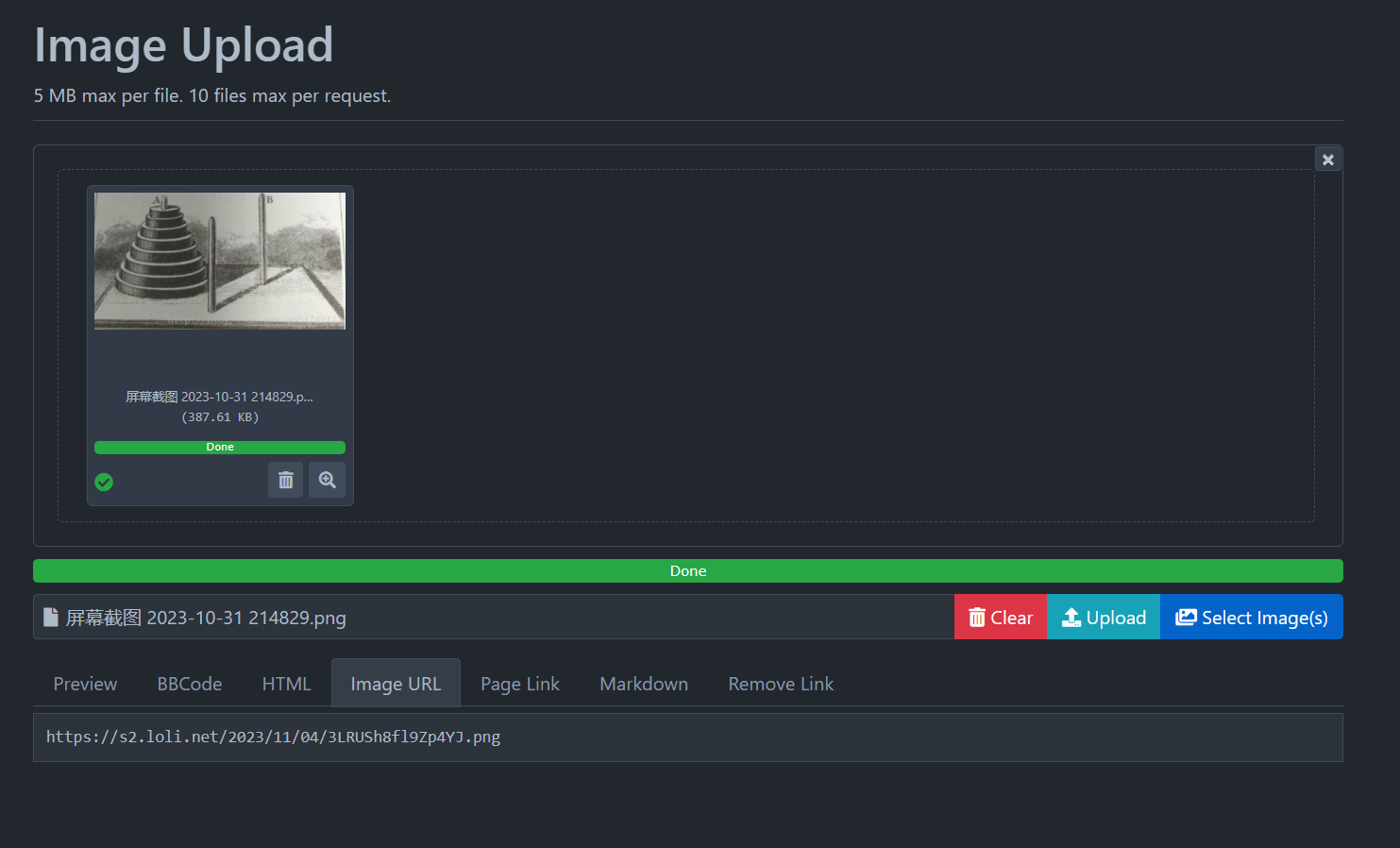
image.png

我们把这个链接复制到Markdown中就可以插入博客了

image.png

  • 链接

我们需要点击一个链接，然后跳转到别的网站

链接的语法非常简单，就是图片去掉一个感叹号

[显示的文字](链接)

image.png

假设我们要书写一篇题解，可以用 # 把题解分成几部分

  • Link 题目链接
  • Question 题目简述
  • Solution 题目解法
  • Code 代码

当然，这个框架仅供参考

对拍

一道题目，往往有一种比较优的解法，能满足所有的数据范围，有一种比较劣的解法(暴力)，能满足部分数据范围

当我们遇到一个代码调不出来时，我们可以考虑对拍

对拍就是用一个暴力来验证我们答案未知的代码

我们通过对拍就可以找到一组小的错误数据，然后用Debug调试排查错误

我们以 A+B problem 为例

假设现在我们有两份代码

正解代码: A.cpp

#include <cstdio>
using namespace std;
int main()
{
    int a, b;
    scanf("%d%d", &a, &b);
    printf("%d\n", a + b);
    return 0;
}

暴力代码: A0.cpp

#include <cstdio>
using namespace std;
int main()
{
    int a, b;
    scanf("%d%d", &a, &b);
    int ans = 0;
    int i;
    for (i = 1; i <= a; i++)
        ans++;
    for (i = 1; i <= b; i++)
        ans++;
    printf("%d\n", ans);
    return 0;
}

显然，下面的代码时间复杂度要大一些(laugh)

我们不能每次都手动打开Devc++，然后手动输入一组数据，所以需要加入文件读写

文件读入 freopen("A.in","r",stdin);

文件输出 freopen("A.out","w",stdout);

freopen(文件名,输入/输出,输入输出流)

我们在 int main() 之后加上这条语句

A.cpp

#include <cstdio>
using namespace std;
int main()
{
	freopen("A.in","r",stdin);
	freopen("A.out","w",stdout); 
    int a, b;
    scanf("%d%d", &a, &b);
    printf("%d\n", a + b);
    return 0;
}

A0.cpp

#include <cstdio>
using namespace std;
int main()
{
	freopen("A.in","r",stdin);
	freopen("A0.out","w",stdout); 
    int a, b;
    scanf("%d%d", &a, &b);
    int ans = 0;
    int i;
    for (i = 1; i <= a; i++)
        ans++;
    for (i = 1; i <= b; i++)
        ans++;
    printf("%d\n", ans);
    return 0;
}

之后我们新建一个输入文件 A.in ，输入数据，并且运行两段代码

image.png

image.png

运行后发现多出了两个 out 文件，分别是两个代码的输出文件

image.png

打开两个文件，发现一样，说明两个代码对于这个输入有着相同的输出

我们需要继续检测其他的输入，但是我们不可能每次手动输入数据，所以需要写一个代码来帮助我们随机生成数据

新建一个 make_data.cpp 用于生成数据

由于要随机生成，所以我们要使用一个函数 rand()

这个函数能生成一个 \([0,32767]\) 的数，\(32767=2^{15}-1\)

一般我们需要生成一个 在 \(int\) 类型范围内的数，所以要把 rand() 的范围扩大

观察 rand() 能生成一个 15 位二进制的数，但是 int 类型有 32 位，所以至少需要用 3 次 rand() 才能把 int 的32 位填满

int brand(){
	return (rand()<<16)+(rand()<<1)+(rand()&1);
}

brand() 函数就能生成一个 \([0,2147483647]\) 的数了

假设我们需要生成一个 \([0,10]\) 的数，我们就 brand()%11 就可以了

假设我们需要生成一个 \([1,10]\) 的数，我们 brand()%10+1

总结如下，如果生成的数的范围在 \([L,R]\) 那么就 brand()%(R-L+1)+L

接下来就可以写 make_data.cpp 了

#include<cstdio>
#include<cstdlib>
#include<windows.h>
using namespace std;
int brand(){
	return (rand()<<16)+(rand()<<1)+(rand()&1);
}
int main(){
	freopen("A.in","w",stdout);
	srand(GetTickCount());
	int a=brand()%10,b=brand()%10;
	printf("%d %d\n",a,b);
	return 0;
}

每运行一次 make_data.exe 就会生成一组新的数据

  • 由于 rand() 是基于秒数的伪随机数，当一秒钟运行两次 make_data.exe 输出的数据是一样的，所以使用 srand(GetTickCount()) 来改成毫秒级

之后，我们的流程应该是这样

  • 点击 make_data.exe 生成一个新的 A.in
  • 分别点击 A.exe 和 A0.exe 来得到两个代码的答案 A.out 和 A0.out
  • 对比 A.out 和 A0.out ，如果相同就重复第一步，如果不同，那就说明这组数据是一组错的样例

每次重复这样的过程太繁琐，能不能写一个代码帮助我们完成这个过程，答案是可以的

我们新建一个 check.bat

@echo off
:loop
A.exe
A0.exe
fc A.out A0.out
if errorlevel==1 pause
goto loop
  • @echo off 关闭多余信息
  • :loop 为一个标记
  • A.exe A0.exe 运行两个 exe
  • fc 为比较函数
  • 返回值在 errorlevel 中，如果相同，errorlevel为 \(0\) 不同为 \(1\)
  • pause 暂停
  • goto loop 跳到 loop 标记

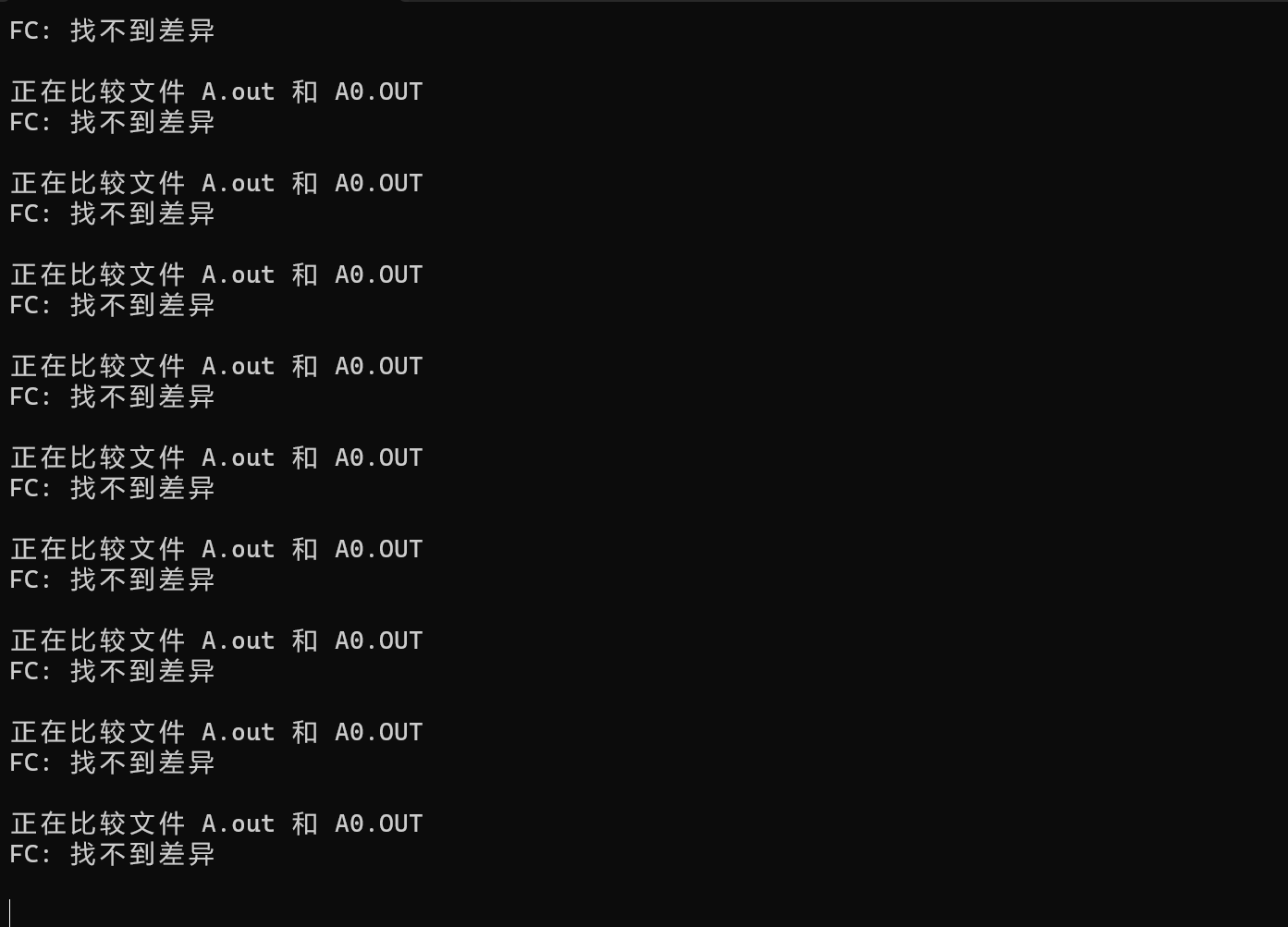
image.png

如果一直不停，说明两个代码几乎没有区别，可以把数据范围放大

如果还是不停，那么可以考虑特殊的边界情况有没有考虑到

我们把 A.cpp 进行一些改动，让他和 A0.cpp 不一样

#include <cstdio>
using namespace std;
int main()
{
	freopen("A.in","r",stdin);
	freopen("A.out","w",stdout); 
    int a, b;
    scanf("%d%d", &a, &b);
    if(a<5&&b<5) printf("11");
    printf("%d\n", a + b);
    return 0;
}

当 \(a<5\) 且 \(b<5\) 时程序会出错

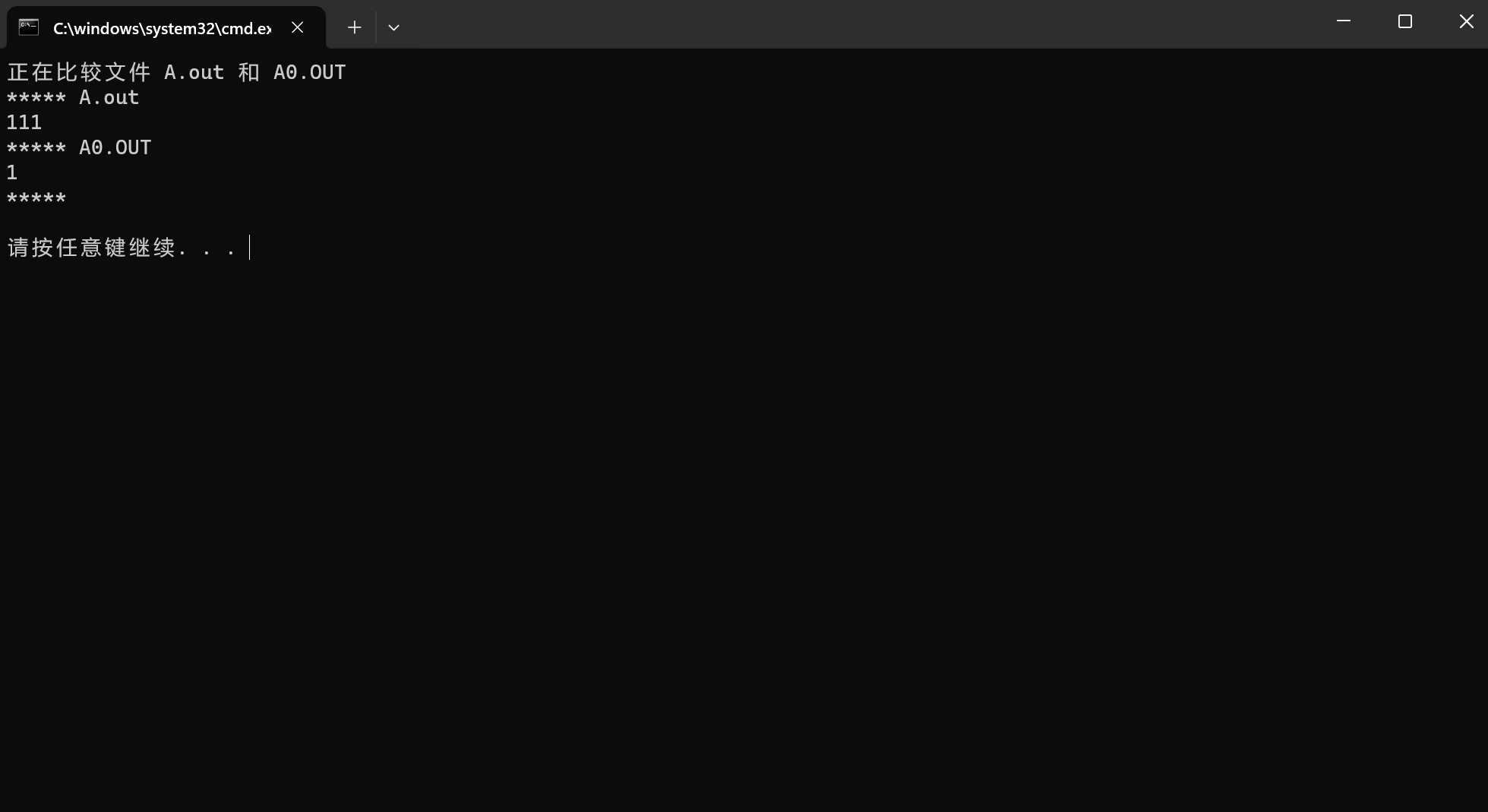
image.png

就会停下来了

之后，就可以利用这个代码进行调试，查错了

补充：

  • 随机也可以采用其他随机生成类，例如 std::mt19937

Debug

在运行程序的时候，总是莫名其妙就结束了，我们也不知道哪里出问题了，有一种方法，能够帮助我们一步一步的运行程序，并且监视变量

接下来以 Dev-C++ 和一个计算阶乘的代码来演示

#include<bits/stdc++.h>
using namespace std;

int Fac(int x){
	int ret=1;
	for(int i=1;i<=x;i++)
		ret*=i;
	return ret;
}
int main(){
	int N;
	cin>>N;
	for(int i=1;i<=N;i++){
		int now;
		cin>>now;
		cout<<Fac(now)<<endl;
	}
	return 0;
}

新建一个断点，代码运行到断点的时候就会停下

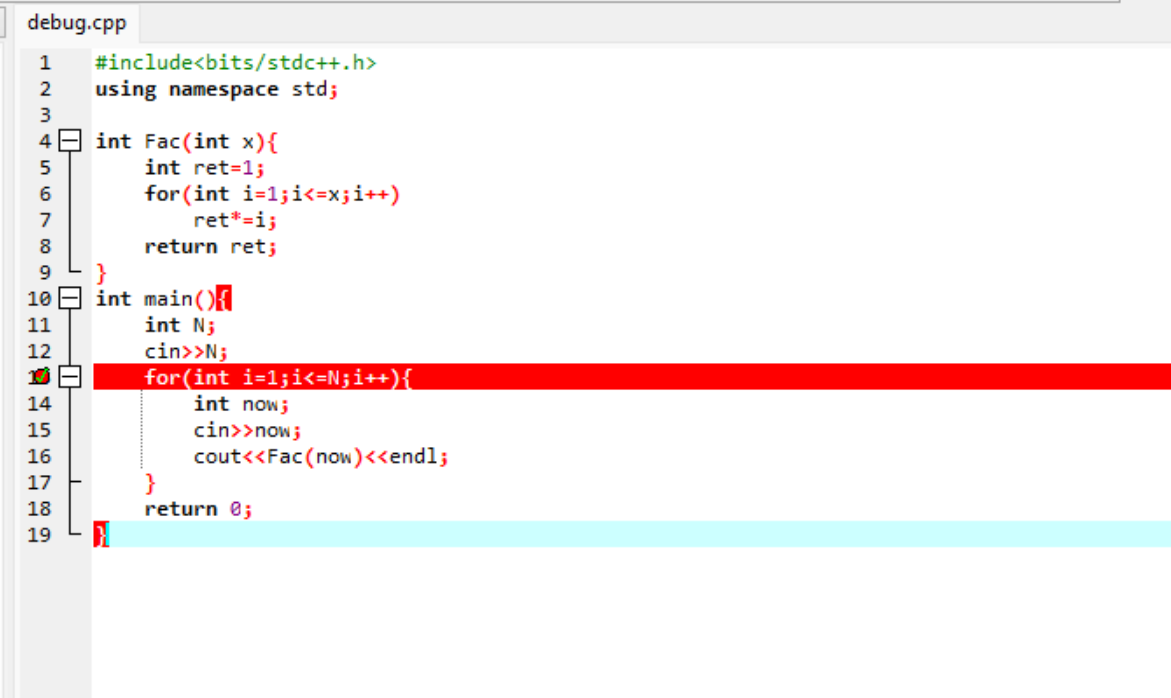
image.png

添加查看就是查看我们需要监视的变量

image.png

输入 5 ,可以观察到 \(N\) 的值已经变成 \(5\) 了

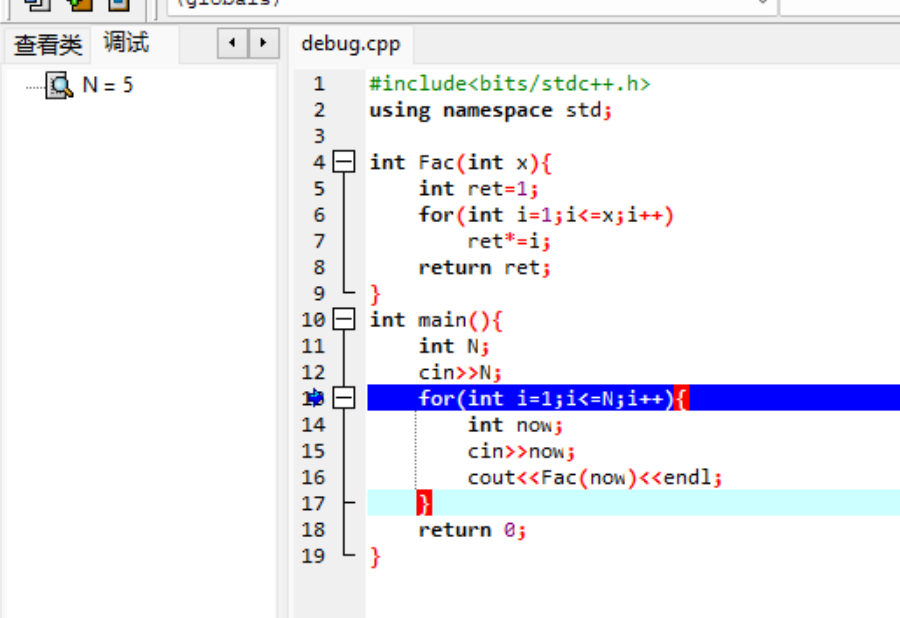
image.png

发现每次调试都需要手动输入数据，所以建议加上文件输入

image.png

然后进入调试就可以不用每次输入了，调试往下进行有两种方式

  • 下一步：更可以理解成下一行（不进入函数）
  • 单步调试：需要进入函数

已知 Fac(x) 返回的是 x 的阶乘，所以我们运行下一步，就可以得到输出的答案

如果我们想要进入 Fac(x) 函数一探究竟，就使用 单步调试

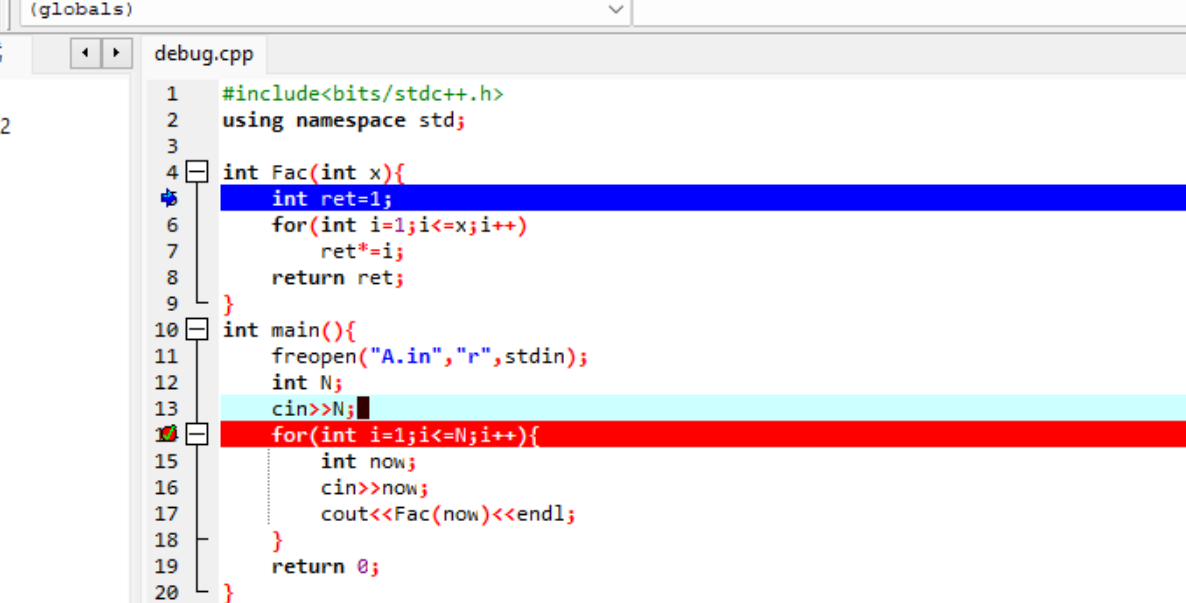
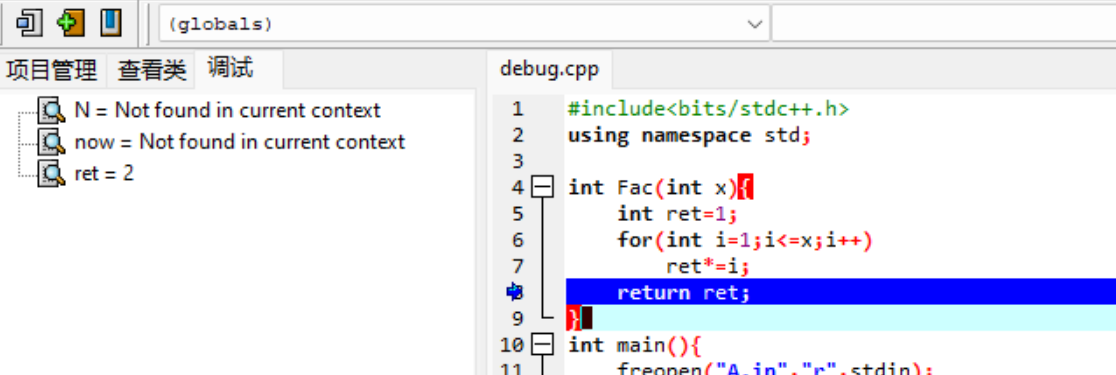
image.png

image.png

通过添加查看，就可以观察到阶乘运行的过程了

可以通过观察程序运行的过程和变量，就可以查出错误了

注意：

  • Dev-C++ 在stl，string等函数会出现问题，建议 使用 vscode ，visual stdio 等其他编译器，或尽量使用静态数组
  • 当数组过大的时候，调试会变得很卡，调试时可以把数组大小减小
  • 添加查看不仅仅可以查看变量，也可以查看表达式，例如 (a+b)/2

时间复杂度

我们把加，减，乘，除，访问变量，这样的基本操作定义为一次基本操作

不同计算机由于硬件的差距，每秒钟可以运行的基本操作的次数是不一样的，一般来说，计算机一秒钟运行次数在 \(3\times 10^8\) 此左右

对于一个代码，我们可以通过计算它执行基本操作的次数来大概估计出代码的运行的时间

题目中，我们常常需要读入一个 \(N\) ，然后进行一系列操作给出答案，其中 \(N\) 就叫数据规模，我们需要给出一个包含于 \(N\) 的式子来表示基本操作的次数，这个过程就叫做估计时间复杂度

例如
C1.cpp

#include<bits/stdc++.h>
using namespace std;
int main(){
    int N;
    cin>>N;
    int a=0;
    for(int i=1;i<=N;i++){
        a++;
    }
    return 0;
}

我们很容易可以知道 基本操作数\(=N\)

C2.cpp

#include<bits/stdc++.h>
using namespace std;
int main(){
    int N;
    cin>>N;
    int a=0;
    for(int i=1;i<=N;i++){
        for(int j=1;j<=N;j++){
            a++;
        }
    }
    return 0;
}

这个也很简单，\(a\) 被加了 \(N^2\) 次，所以基本操作数\(=N^2\)

因为程序中存在 if 语句等分支结构，所以即使 \(N\) 相同，不同数据的时间复杂度也是不一样的

算法竞赛中，如果有一组数据超时了，那么整道题就会被判为超时，所以我们要求对于 \(N\) 的最大复杂度，用符号 \(O()\) 表示

例如，上面的例子就可以被表示为 \(O(N),O(N^2)\)

题目中，\(N\) 常常非常大

所以，一些常数和系数可以忽略不记 \(O(N+100)\) 可以看成和 \(O(N)\) 一样的，\(O(10N)\) 看成和 \(O(N)\) 是一样的

这里要注意，一道题目中往往不是由一个量来决定时间复杂度的

例如
C3.cpp

#include<bits/stdc++.h>
using namespace std;
int main(){
    int N,M;
    cin>>N>>M;
    int a=0;
    for(int i=1;i<=N;i++){
        for(int j=1;j<=M;j++){
            a++;
        }
    }
    return 0;
}

这里的时间复杂度就是 \(O(N\times M)\)

有些时间复杂度往往不是那么显然，需要多做题积累

C4.cpp

#include<bits/stdc++.h>
using namespace std;
int main(){
    int N;
    cin>>N;
    int a=0;
    for(int i=1;i<=N;i*=2){
        a++;
    }
    return 0;
}

这个代码中 \(i\) 每次都变成自己的两倍，所以时间复杂度就是 \(log_2N\)

求这个式子可以利用换底公式 \(log_2N=\frac{lgN}{lg2}\) 使用系统自带的计算器就可以计算出这个答案了

再看一个例子 C5.cpp

#include<bits/stdc++.h>
using namespace std;
int main(){
    int N;
    cin>>N;
    int a=0;
    for(int i=1;i<=N;i++){
        for(int j=1;j<=N;j+=i){
            a++;
        }
    }
    return 0;
}

观察到内循环每次需要执行 \(N/i\) 次

所以，我们能用式子算出循环次数

\[\frac{N}{1}+\frac{N}{2}+\frac{N}{3}+\cdots+\frac{N}{N}=N(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{N})=N\times H_N \]

其中 \(H_N\) 为调和级数的和，当 \(N\) 特别大的时候 \(H_N \sim ln(n)\)

所以这个的时间复杂度就是 \(O(NlnN)\)

其中有一些比较常见的时间复杂度

\[O(n),O(n^2),O(n^3),O(nlogn),O(nlog^2n),O(2^n),O(n!) \]

这些时间复杂度所对应的 \(N\) 的最大值都应该熟记

空间复杂度

与时间复杂度类似的，也有空间复杂度

题目中往往都会给出

image.png

那么我们如何计算我们程序所消耗的空间，也就是空间复杂度呢

已知一个 int 类型占 4 个字节， long long 8 个字节， double 8 个字节，char 1 个字节

一个数组所占的大小就是 数组长度 \(\times\) 单个字节所占字节

例如 int a[1000000] 所占空间 就是 \(1000000 \times 4 = 4000000 Byte\)

\(4000000Byte = 4000000/1024/1024 MB = 3.8MB\)

一般我们都需要把数组开大一点点，防止访问到没有定义的内存，一般我们多开 \(5\) 个单位

如果 \(N\) 的最大值为 \(1e6\) 我们就可以定义一个常量 maxn 的值，为 1e6+5

const int maxn=1e6+5

然后在定义数组的时候使用 maxn

int a[maxn]={0};

如果是多维数组的话，就把每一维乘起来就好了

char c[105][2005]所占的内存就是

\(105 \times 2005\times 1 /1024/1024 \ MB\)

如果要开动态数组和其他动态开内存的容器，如 vector，map，set，他们的空间复杂度往往与时间复杂度有关，怕爆内存的可以使用 vector 来代替静态数组

注意：

  • 头文件也占一定的内存，大数组不能开的太满
  • 递归的时候所占的内存与系统栈的深度有关，所以也要保留一定的空间

标签：std,int,复杂度,Blog,cpp,Debug,Week0,include,我们
From： https://www.cnblogs.com/martian148/p/17831185.html

相关文章

  • 博客园cnblogs的代码折叠
    实现折叠的代码如下：<details><summary>查看代码</summary><pre><code>这里写需要被折叠的代码</code></pre></details>效果如下：查看代码这里写需要被折叠的代码参考链接：https://www.cnblogs.c......
  • 无涯教程-Dart - 调试(Debug)
    开发人员时不时地在编码时犯错误，程序中的错误称为错误，查找和修复错误的过程称为调试，并且是开发过程中的正常部分，本节介绍可帮助您完成调试任务的工具和技术。添加断点考虑以下代码片段。(TestString.dart)voidmain(){inta=10,b=20,c=5;c=c*c*c;p......
  • Debug
    error：error:Couldn'tapplyexpressionsideeffects:Couldn'tdematerializearesultvariable:couldn'treaditsmemoryreason：variablegotoptimizedouthowtosolveituseoption-O0toavoidoptimizingReference......
  • dsBlog前后台博客系统
    博客简介：本博客采用SpringBoot+LayUI做为基础，进行的博客系统开发，与boot+vue相比，更为适合开发简单的系统，并且更容易上手，简单！高效！更易上手！SpringBoot+LayUI:快速开发：LayUI是一个简单的UI框架，它提供了易于使用的组件，可以快速构建界面。搭配SpringBoot，你可以迅速开发出后台......
  • idea中的 debug 中小功能按钮都代表的意思
    1.stepover步过----->一行一行的往下走,如果这一行中有方法那么不会进入该方法,直接一行一行往下走,除非你在该方法中打入断点2.stepinto步入--->可以进入方法内部,但是只能进入自己写的方法内部,而不会进入方法的类库中3.Forcestepinto强制步入---->可以步入任何方法,包括......
  • scrapy解析数据，配置文件，整站爬取cnblogs，持久化
    1scrapy解析数据......
  • vscode python remote debug极速入门
    本文适用范围主要适用于debugpython程序，尤其是深度学习刚入门需要使用remote连接到linux进行程序运行，想调试一下的同学。当然非深度学习也可以参考食用本文哈哈哈。极速入门版提前准备：代码仓库已经拉取到linux上面，且已经知道运行的方式。比如：项目的启动命令为：pythonpret......
  • cnblogs 侧边栏
    <scripttype="text/javascript">window.cnblogsConfig={info:{name:'Martian148',//用户名||不配置默认取博客园名称startDate:'2018-10-13',//入园时间，年-月-日。入园时间查看方法：鼠标停留园龄时间上，会显示入园时间......
  • JVM系列-第7章-对象的实例化内存布局与访问定位-cnblog
    title:JVM系列-第7章-对象的实例化内存布局与访问定位tags:-JVM-虚拟机categories:-JVM-1.内存与垃圾回收篇keywords:JVM，虚拟机。description:JVM系列-第7章-对象的实例化内存布局与访问定位。cover:'https://gitee.com/youthlql/randombg/raw/master/lo......
  • JVM系列-第9章-StringTable(字符串常量池)-cnblog
    title:JVM系列-第9章-StringTable(字符串常量池)tags:-JVM-虚拟机categories:-JVM-1.内存与垃圾回收篇keywords:JVM，虚拟机。description:JVM系列-第9章-StringTable(字符串常量池)。cover:'https://gitee.com/youthlql/randombg/raw/master/logo/jvm.png......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99