231110练习赛总结

T1 Alchemy

几点反思：

1. 对 最大 不敏感，确定了题目涉及 \(DAG\) 之后只知道盲目用 \(topsort\) 处理，而没有想到二分, 积累经验。
2. 想复杂了，其实根本不用 \(topsort\), 因为限制了边的起点一定小于终点，且制造每个金属只有一种方案，也就是说所有指向该点的边同属于一种方案，可以直接倒序（线性）处理流量，更新时用一下邻接表就可以）
3. 做得很好的一点是早早就反映出来正着考虑传递关系不好做，要倒过来从终点开始流。
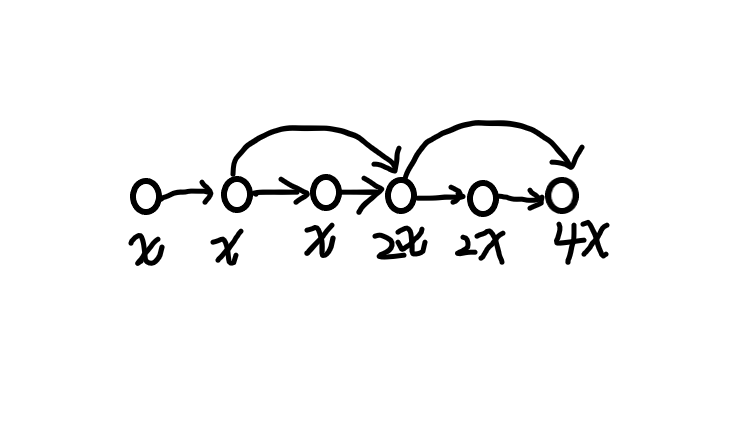
4. 要特判剩余总需求已经远远大于总的可支配流量的情况(可能会爆long long)，因为剩余需求可能回成指数级增长，如图：

#include<bits/stdc++.h>
#define F(i,l,r) for(int i=l;i<=r;++i)
#define G(i,r,l) for(int i=r;i>=l;--i)
#define int long long 
using namespace std;
const int N=110;
int a[N],s[N],b[N],n,m;
vector<int> g[N];
inline bool chk(int x){
	F(i,1,n) b[i]=(i==n)?x:0;//初始化每个点还未处理的流量 
	G(i,n,1){
		if(b[i]<=a[i]) continue;//需求<拥有,一定满足
		if(b[i]>a[i] && g[i].empty()) return 0;//需求>拥有,且传不出去了,必死无疑 
//		if(b[i]-a[i]>s[i-1]) return 0;//剩余总需求>剩下总拥有,必死无疑
		for(auto j:g[i]) {
			b[j]+=b[i]-a[i];//更新流量
			if(b[j]>s[n]) return 0;//剩余总需求>总拥有,必死无疑(两种写法任选其一来特判即可,因为流量需求可能会成指数级增长)
		}
	} return 1;//bi:到节点i时还有多少流量没有处理(所以若上一步处理出来是负流量,不需要更新过去,之前的步骤与步骤之间是相互独立的) 
}
signed main(){
    freopen("alchemy.in", "r", stdin);
    freopen("alchemy.out", "w", stdout);
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin>>n;
	F(i,1,n) cin>>a[i],s[i]=s[i-1]+a[i];//2.预处理前缀和 
	cin>>m; int x,y,z;
	F(i,1,m){
		cin>>x>>y;
		while(y--){
			cin>>z;
			g[x].push_back(z);//连边(反向)
		}
	}
	int l=a[n]-1,r=s[n]+1,mid;//1.  l&r 的设置
	while(l+1<r){
		mid=l+r>>1;
		if(chk(mid)) l=mid;
		else r=mid;
	}
	cout<<l;
	return 0; 
} 

T2 Visits

反思：没有意识到其实每个点的出度只有 \(1\).

对于每个$ 1\le i\le N$，伙伴 \(i\) 想要访问伙伴 \(a_i(a_i\neq i)\)。

这样一来整张图就变成了一堆环，环周围挂了一堆树。

所以根本没有非环非树的一般情况出现。

认清楚这一点之后就好做了。

最优的访问顺序是：树上的点自底向上的话就都能访问到，环上就删去权值最小的那条边即可。

可以用“最大生成树”实现环上避开最小边的过程。

#include<cstdio>
#include<algorithm>
#define F(i,l,r) for(int i=l;i<=r;++i)
#define G(i,r,l) for(int i=r;i>=l;--i)
#define ll long long
using namespace std;
const int N=1e5+5;
struct node{ int u,v,w; bool operator < (const node &other) const{ return w>other.w; } }e[N];
int n,fa[N];
ll sum=0;
inline int get(int x){ return (fa[x]!=x)?fa[x]=get(fa[x]):x; }
int main(){
	freopen("visits.in","r",stdin);
	freopen("visits.out","w",stdout);
	scanf("%d",&n);
	int x,y;
	F(i,1,n) fa[i]=i,scanf("%d %d",&x,&y),e[i]=node{i,x,y};
	std::sort(e+1,e+n+1);
	F(i,1,n){
		int u=e[i].u,v=e[i].v,w=e[i].w;
		int fx=get(u),fy=get(v);
		if(fx==fy) continue;
		fa[fx]=fy,sum+=w;		
	}
	printf("%lld",sum);
	return 0;
}

T3 COW Operations

思考后发现以下性质：

1.因为操作2，所以

（1）任意两种相邻字符可以交换顺序，比如：OW --> WCW --> WO

（2）操作2的逆操作可以通过一次操作1+一次操作2来实现，比如：OW--> CWW --> C

2.由1.（1）进一步发现：对于一段区间中的 C,W,O 来说，无论相对位置如何，都是可以消掉的。

到这里就已经可以做了：一段区间能不能消成单个C，取决于三种字符的个数，再进一步地，取决于个数的奇偶性。

#include<bits/stdc++.h>
#define F(i,l,r) for(int i=l;i<=r;++i)
#define G(i,r,l) for(int i=r;i>=l;--i)
using namespace std;
const int N=2e5+5;
int w[N],o[N],c[N],q,l,r;
char s[N];
int main(){
	freopen("cowoper.in","r",stdin);
	freopen("cowoper.out","w",stdout);
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin>>(s+1); int n=strlen(s+1);
	F(i,1,n){
		w[i]=w[i-1],c[i]=c[i-1],o[i]=o[i-1];
		if(s[i]=='W') ++w[i];
		else if(s[i]=='C') ++c[i];
		else ++o[i];
	}
	cin>>q;
	while(q--){
		cin>>l>>r;
		int A=(w[r]-w[l-1])&1,B=(o[r]-o[l-1])&1,C=(c[r]-c[l-1])&1;
		if((!A) && (!B) && C) cout<<'Y';
		else if(A && B && (!C)) cout<<'Y';
		else cout<<'N';
	}
	return 0;
}

3. 还有另一种方法，进一步推导：
   将CWO分别映射成123，再求前缀异或和，可以很好地实现操作1的”消“和操作2的”替换“。

“消除相邻字符”，这很像是异或可以完成的事情，比如 \(1 \oplus 1=0\)

"将一个字符换成另外两种字符",这也很像是异或，比如 \(1 \oplus 2 =3\)

区间异或是可以通过前缀异或和得到的，因此问题就变成了区间异或和是不是 \(1\).

#include<bits/stdc++.h>
#define F(i,l,r) for(int i=l;i<=r;++i)
#define G(i,r,l) for(int i=r;i>=l;--i)
using namespace std;
const int N=2e5+5;
char s[N];
int sum[N],q,l,r;
int main(){
	//1 2 3
	//C O W
	freopen("cowoper.in","r",stdin);
	freopen("cowoper.out","w",stdout);
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin>>(s+1); int n=strlen(s+1); 
	F(i,1,n) {
		int x=(s[i]=='C')?1:((s[i]=='O')?2:3);
		sum[i]=sum[i-1]^x;		
	}
	cin>>q;
	while(q--){
		cin>>l>>r;
		if((sum[r]^sum[l-1])==1) cout<<'Y';
		else cout<<'N';
	}
	return 0;
}

最后还有一种 [@逆行伐仙]( 逆行伐仙 - 博客园 (cnblogs.com) ) 大佬的写法，是上面第二种的变形：（不映射，直接对三种字符进行异或判断，主要多了一个空字符，稍微不好写一点）

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+20;
int n;
char c[N],tt='C'^'O'^'W',sum[N];
inline char suan(char x,char y){
	if(x==y) return ' ';
	else if(x==' ') return y;
	else if(y==' ') return x;
	return tt^x^y;
}
int main(){
	freopen("cowoper.in","r",stdin);freopen("cowoper.out","w",stdout);
	scanf("%s",&c);
	sum[0]=' ',sum[1]=c[0];
	int len=strlen(c);
	for(int i=2;i<=len;i++) sum[i]=suan(sum[i-1],c[i-1]);
	scanf("%d",&n);
	for(int i=1,l,r;i<=n;i++){
		scanf("%d%d",&l,&r);
		if(suan(sum[r],sum[l-1])=='C') putchar('Y');
		else putchar('N');
	}
}

总结：此题主要首先得分析出字符可互换（这个我做到了），紧接着要分析出对操作后，一段区间结果的求解来说，字符位置不重要，只关心个数（这一点我没有意识到）

要积累经验,特别是一道题有哪些信息影响求解，哪些信息看似影响，实则与结果无关。

还有异或的应用场景：消除，替换。

“在动中寻找不变量”——PF

练习赛总结

真的明显感觉思维太不行了，遇到这种码量不大，稍微变一点形，考一点思维的题就和同学们拉开很大差距了。

要多刷题，多积累经验，训练思维！尽量一题多解全部吃透！

提高效率！合理安排时间，做好计划！