队列介绍
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。队列中没有元素时,称为空队列。
队列的特点是先进先出(FIFO),下面是队列的结构图:

常用方法
既然是队列,那么入队和出队操作是必不可少的,除此之外,还需要其他api,下面是Queue的接口:
/**
* 队列接口
* @author mingshan
*
* @param <E>
*/
public interface Queue<E> {
/**
* 添加元素, 如果没有可用的空间,抛出IllegalStateException异常
* @param e 将要添加的元素
* @return
*/
boolean add(E e);
/**
* 添加元素。成功时返回 true,如果当前没有可用的空间,则返回 false,不会抛异常
* @param e 将要添加的元素
* @return
*/
boolean offer(E e);
/**
* 获取并移除此队列的头部,如果队列为空,则返回null
* @return 头部元素
*/
E poll();
/**
* 获取队列头部元素, 不移除头部元素
* @return 头部元素
*/
E peek();
/**
* 判断队列是否为空
* @return
*/
boolean isEmpty();
/**
* 获取队列的长度
* @return 队列的长度
*/
int size();
/**
* 清空队列
*/
void clear();
}
下面来看看这些方法如何实现,现在还不考虑锁的问题,java.util.concurrent.ArrayBlockingQueue这个类有具体的实现,有空分析分析这个类的源码。
构造函数和成员变量
顺序队列默认把元素存到数组里,所以这里用数组来保存队列里的元素,代码如下:
// 队列内部数组默认容量
private static final int DEFAULT_SIZE = 10;
// 队列内部数组的容量
private int capacity;
// 保存元素的数组
private Object[] elements;
// 指向队列头部
private int head;
// 指向队列尾部
private int tail;
在构造函数里面初始化队列的大小
/**
* 默认构造函数初始化
*/
public ArrayQueue() {
capacity = DEFAULT_SIZE;
elements = new Object[capacity];
}
/**
* 指定队列内部数组容量进行初始化
* @param capacity 指定容量
*/
public ArrayQueue(int capacity) {
this.capacity = capacity;
elements = new Object[capacity];
}
/**
* 指定队列的第一个元素进行初始化
* @param e 队列的第一个元素
*/
public ArrayQueue(E e) {
this.capacity = DEFAULT_SIZE;
elements = new Object[capacity];
elements[0] = e;
tail++;
}
/**
* 指定队列的第一个元素和容量进行初始化
* @param e 队列的第一个元素
* @param capacity 队列内部数组容量
*/
public ArrayQueue(E e, int capacity) {
this.capacity = capacity;
elements = new Object[capacity];
elements[0] = e;
tail++;
}
入队
在入队的时候,其实有两种选择,如果队列满的话,抛出异常,或者等待其他元素出队后再进行入队。
add(E e)
add方法就是实现第一种,如果没有可用的空间,抛出IllegalStateException异常,代码如下:
@Override
public boolean add(E e) {
if (e != null) {
// 获取当前的数组的长度
int oldLength = elements.length;
// 如果原来数组的长度小于当前需要的长度,那么直接抛异常IllegalStateException
if (oldLength < tail + 1) {
throw new IllegalStateException("Queue full");
} else {
elements[tail++] = e;
}
} else {
throw new NullPointerException();
}
return true;
}
先获取队列的大小,如果队列的大小小于当前需要的空间,那么直接抛异常IllegalStateException,否则正常入队。
假溢出
我们在利用数组实现队列的时候,发现数组队列会出现假溢出问题,即队列还没有满,但不能再往队列中放入元素了,如下图所示:
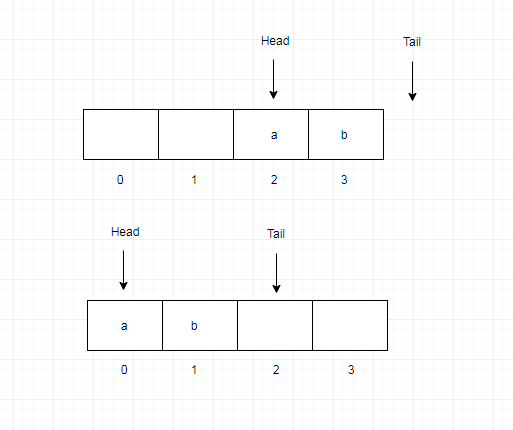
在数据进行出队的时候,每一个元素出队,指向队列头元素的head就会向后移动,导致head之前的元素被“遗忘”了,无法再次利用。
当然,我们可以对数组队列进行一些优化。在插入元素的时候,我们检查一下tail是否已经指向了队尾,如果指向了队尾并且head不等于0的情况下,说明发生了假溢出,需要进行元素迁移工作,将head和tail之间的元素整体移动到 0 到 tail - head 的位置,这样就可以避免假溢出问题了(还是上面的图),优化后的代码如下:
/**
* 由于数组队列存在假溢出问题,所谓要进行数据搬运
*/
@Override
public boolean add(E e) {
Objects.requireNonNull(e);
if (tail == capacity) {
if (head == 0) {
// 证明队列是满的
throw new IllegalStateException("Queue full");
}
// 如果head 不等于0,证明head之前的空间是空着的,所以需要进行数据搬运
for (int i = head; i < tail; i++) {
elements[i - head] = elements[i];
}
// 搬运完更新head 和 tail
head = 0;
tail -= head; // tail = tail - head
}
// 正常操作
elements[tail++] = e;
return true;
}
offer(E e)
入队操作。成功时返回 true,如果当前没有可用的空间,则返回 false,不会抛异常,由于这里没有用到锁,也就暂时不考虑等待入队了,代码如下:
@Override
public boolean add(E e) {
if (e != null) {
// 获取当前的数组的长度
int oldLength = elements.length;
// 如果原来数组的长度小于当前需要的长度,那么直接抛异常IllegalStateException
if (oldLength < tail + 1) {
throw new IllegalStateException("Queue full");
} else {
elements[tail++] = e;
}
} else {
throw new NullPointerException();
}
return true;
}
根据前面的假溢出问题分析,优化后的代码如下:
@Override
public boolean offer(E e) {
Objects.requireNonNull(e);
if (tail == capacity) {
if (head == 0) {
// 证明队列是满的
return false;
}
// 如果head 不等于0,证明head之前的空间是空着的,所以需要进行数据搬运
for (int i = head; i < tail; i++) {
elements[i - head] = elements[i];
}
// 搬运完更新head 和 tail
head = 0;
tail = elements.length;
}
// 正常操作
elements[tail++] = e;
return true;
}
出队
poll()
获取并移除此队列的头部,如果队列为空,则返回null,代码如下:
@SuppressWarnings("unchecked")
@Override
public E poll() {
if (!isEmpty()) {
E value = (E) elements[head];
// 移除头部元素
elements[head] = null;
head++;
return value;
}
return null;
}
peek()
获取队列头部元素, 不移除头部元素,代码如下:
@SuppressWarnings("unchecked")
@Override
public E peek() {
if (!isEmpty()) {
return (E) elements[head];
}
return null;
}
清空队列
由于用数组存储队列元素,所以需要将底层数组清空
@Override
public void clear() {
//将底层数组所有元素赋为null
Arrays.fill(elements, null);
head = 0;
tail = 0;
}