已经知道坑点的情况下暴力+正解 想+写还是用了 2h……调试速度太慢了。
所以场上如果想多肝出一道题的话,简单题必须在 10min~40min 结束战斗啊!
以及对于这种数据范围小到一眼就需要分类讨论的题目,一定要多思考不同数据下的差异。
\(k\le 2\) 时不难想到对于每次询问朴素 dp,此时我们选择的传输主机一定不会出链,故可以把询问 \((s,t)\) 从 \(lca\) 拆成两段,对于每一段,设 \(dp_{i,0/1}\) 表示上一个选择的主机为当前节点/当前节点儿子,朴素转移后,最终合并两段答案即可。
显然可以用矩阵描述这个过程,故将树重链剖分后,用线段树维护矩阵乘积即可做到 2log。
\(k=3\) 时,会存在一种情况使得我们选择的主机不在链上:
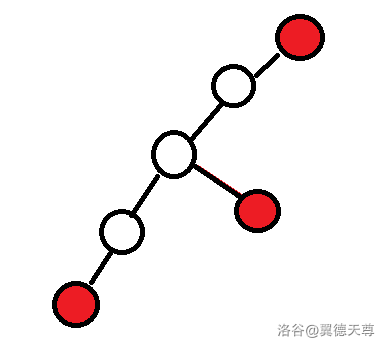
即,我们可能会从离当前节点两格的位置,直接跳到一个离当前节点一格的位置,再跳出去。
不过好在我们可以证明,只有这种情况会选择链外节点,其它情况选择链外节点一定不优。
于是我们可以预处理出对于每个节点 \(i\),儿子内的最小权值 \(s_i\),转移加上可以从距儿子一格的位置,花费 \(s_i\) 的代价到达距当前节点一格的位置即可。注意将两部分答案合并时,我们还可能跳到 \(lca\) 的父亲上,故合并时我们可以修改下 \(lca\) 的转移矩阵,把父亲也考虑进 \(s_{lca}\) 中,合并完再改回去即可。
总时间复杂度 \(O(n\log^2 n)\),且拥有转移矩阵高贵的 \(3^3=27\) 的常数。不过好在树剖常数小,过得还是很轻松的。
标签:P8820,当前,矩阵,节点,即可,2022,lca,CSP,一格 From: https://www.cnblogs.com/ydtz/p/17793948.html