力扣1444.切割后面积最大的蛋糕（贪心）

矩形蛋糕的高度为 h 且宽度为 w，给你两个整数数组 horizontalCuts 和 verticalCuts，其中：

•  horizontalCuts[i] 是从矩形蛋糕顶部到第  i 个水平切口的距离
• verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离

请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后，请你找出 面积最大 的那份蛋糕，并返回其 面积 。由于答案可能是一个很大的数字，因此需要将结果 对 109 + 7 取余 后返回。

示例 1：

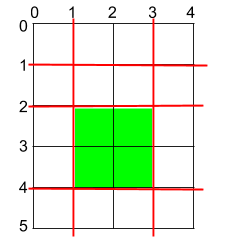
输入：h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
输出：4 
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色的那份蛋糕面积最大。

示例 2：

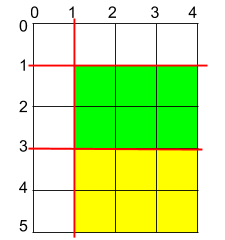
输入：h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
输出：6
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色和黄色的两份蛋糕面积最大。

示例 3：

输入：h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
输出：9

提示：

• 2 <= h, w <= 109
• 1 <= horizontalCuts.length <= min(h - 1, 105)
• 1 <= verticalCuts.length <= min(w - 1, 105)
• 1 <= horizontalCuts[i] < h
• 1 <= verticalCuts[i] < w
• 题目数据保证 horizontalCuts 中的所有元素各不相同
• 题目数据保证 verticalCuts 中的所有元素各不相同

1.分治法：每次切割都将原来的图分割成两部分，然后对于被分割出来的两部分再进行分割，直到不能分割为止。剪枝：先对分割序列进行排序，这样就可以实现：先从上往下横着切，再从左到右竖着切。这样一来，对于横切部分，划分成上下两半，（若升序排序）上半边已经不会再被切割了，所以对上半边进行递归的时候可以把水平切割队列置空；对于竖切部分同理。

 1 class Solution
 2 {
 3 public:
 4     vector<int> none;
 5     long long max_area = 0;
 6     long long mod = 1e9 + 7;
 7     void divideArea(long long bx, long long by, long long ex, long long ey, vector<int> horizontalCuts, vector<int> verticalCuts)
 8     { // bx、by为区域左上角坐标，ex、ey为区域右下角坐标
 9 
10         if (!horizontalCuts.empty())
11         {
12             int row = horizontalCuts.front();
13             horizontalCuts.erase(horizontalCuts.begin());
14             divideArea(bx, by, row, ey, none, verticalCuts);           // 上部
15             divideArea(row, by, ex, ey, horizontalCuts, verticalCuts); // 下部
16         }
17         else if (!verticalCuts.empty())
18         {
19             int column = verticalCuts.front();
20             verticalCuts.erase(verticalCuts.begin());
21             divideArea(bx, by, ex, column, none, none);         // 左部
22             divideArea(bx, column, ex, ey, none, verticalCuts); // 右部
23         }
24         else
25         { // 切割完毕，更新最大面积
26             max_area = max(max_area, (ey - by) * (ex - bx));
27         }
28     }
29     int maxArea(int h, int w, vector<int> &horizontalCuts, vector<int> &verticalCuts)
30     {
31         sort(horizontalCuts.begin(), horizontalCuts.end());
32         sort(verticalCuts.begin(), verticalCuts.end());
33         divideArea(0, 0, h, w, horizontalCuts, verticalCuts);
34         return max_area % mod;
35     }
36 };

该代码不能通过最后一组用例，因为空间复杂度爆了，暂时没找到优化的点，仅供思路参考。

2.贪心法：我们注意到他的每次切割都是水平或垂直的完全切割，也就是说每次不同方向切割都能相互影响（例如横切过2刀之后，蛋糕被分成了三块，此时竖切一刀，这时的三块蛋糕都会同时受到影响），所以我们只需考虑横切完后的最大间距和竖切完后的最大间距，他们围成的面积就是最大的。

 1 class Solution
 2 {
 3 public:
 4     long long mod = 1e9 + 7;
 5 
 6     long long maxInterval(vector<int> arr, int border)
 7     {
 8         int mmax = border - *arr.rbegin(); //初值为最后一块的长度
 9         int pre = 0;
10         for (int i : arr)
11         {
12             mmax = max(i - pre, mmax);
13             pre = i;
14         }
15         return mmax;
16     }
17     int maxArea(int h, int w, vector<int> &horizontalCuts, vector<int> &verticalCuts)
18     {
19         sort(horizontalCuts.begin(), horizontalCuts.end());
20         sort(verticalCuts.begin(), verticalCuts.end());
21         return maxInterval(horizontalCuts, h) * maxInterval(verticalCuts, w) % mod;
22     }
23 };