原始题目：DeepAR: Probabilistic forecasting with autoregressive recurrent networks
中文翻译：DeepAR:自回归递归网络的概率预测
发表时间：2020年07月
平台：International Journal of Forecasting
文章链接：https://www.sciencedirect.com/science/article/pii/S0169207019301888
开源代码：https://github.com/zhykoties/TimeSeries

摘要

概率预测，即在给定时间序列过去的情况下估计其未来的概率分布，是优化业务流程的关键因素。例如，在零售企业中，预测需求对于在正确的时间、正确的地点获得正确的库存至关重要。在本文中，我们提出了DeepAR，这是一种生成准确概率预测的方法，基于在大量相关时间序列上训练自回归递归网络模型。我们展示了如何将深度学习技术应用于预测，可以克服广泛使用的经典方法所面临的许多挑战。我们通过对几个真实世界预测数据集的广泛实证评估表明，与最先进的方法相比，准确率提高了约15%。

1. 引言

在现实世界的预测问题中，当试图从多个时间序列中联合学习时，经常遇到的一个挑战是不同时间序列的幅度大小差异很大，并且幅度的分布严重偏斜。

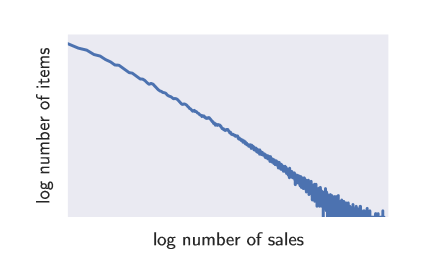
图1：电子商务500K时间序列的商品数量与销售额的对数柱状图，显示电子商务数据集中存在的无标度性质（近似直线）（由于数据的非公开性质，省略了轴标签）。

本文的主要贡献有两方面：

（1）我们提出了一种用于概率预测的RNN架构，对计数数据采用负二项式似然，并对时间序列幅度变化较大的情况进行了特殊处理；（2） 我们在几个真实世界的数据集上实证证明，该模型在一系列输入特征上产生了准确的概率预测，从而表明基于现代深度学习的方法可以有效地解决概率预测问题，这与该领域的普遍看法和[24，17]中报道的混合结果形成了鲜明对比。

2. 相关工作

3. 模型

图2：模型摘要。训练（左）：在每个时间步长t，网络的输入是协变量xi，t，前一时间步长zi，t−1的目标值，以及前一网络输出hi，t−1。然后使用网络输出hi，t=h（hi，t−1，zi，t−2，xi，t，θ）来计算用于训练模型参数的似然性（z|θ）的参数θi，t=θ（hi，t，θ）。对于预测，时间序列zi，t的历史在t＜t0时被输入，然后在t≥t0的预测范围（右）中，绘制一个样本ξzi，t～（·|θi，t）并反馈下一点，直到预测范围t=t0+t结束，生成一个样本轨迹。重复该预测过程产生表示联合预测分布的许多迹线。

3.1 似然模型

似然性\(l(z|θ）\)决定了“噪声模型”，并且应该选择它来匹配数据的统计特性。在我们的方法中，网络直接预测下一个时间点的概率分布的所有参数θ（例如均值和方差）。

网络预测概率分布的参数，比如高斯分布的均值\(\mu\)和方差\(\theta\)

对于本文中的实验，我们考虑两种选择，实数数据的高斯似然和正计数数据的负二项式似然。也可以很容易地使用其他似然模型，例如单位区间数据的贝塔似然、二进制数据的伯努利似然或者它们的混合以处理复杂的边际分布，只要可以廉价地获得分布中的样本，并且可以评估对数似然及其梯度wrt.参数。

我们使用高斯似然的均值和标准差θ=（μ，σ）对其进行参数化，其中均值由网络输出的仿射函数给出，标准差通过应用仿射变换和softplus激活来获得，以确保σ>0：

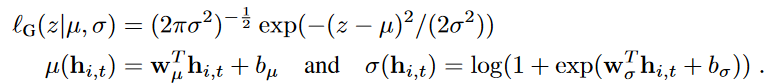
3.2 训练

给定时间序列的数据集\(\{z_{i,1:T}\},i=1,...,N\)和相关协变量\(x_{i,1:T}\)，通过选择预测范围中的已知的时间范围获得\(z_{i,t}\)，模型的参数\(\Theta\)，包括RNN \(h(·)\)的参数和\(θ(·)\)参数，可以通过最大化对数似然来学习。

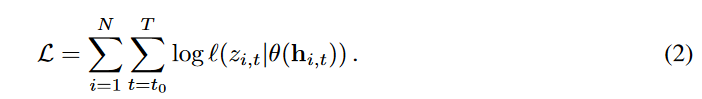
3.3 幅度控制

将该模型应用于显示如图1所示的尺度幂律的数据提出了两个挑战。

首先，由于模型的自回归性质，自回归输入zi，t−1以及网络的输出（例如μ）都直接与观测值zi，t成比例，但其间网络的非线性具有有限的操作范围。因此，在没有进一步修改的情况下，网络必须学会将输入缩放到输入层中的适当范围，然后在输出处反转这种缩放。我们通过将自回归输入zi，t（或ξzi，t）除以项目相关的标度因子\(\nu_i\)来解决这个问题，并反过来将标度相关的似然参数乘以相同的因子。例如，对于负二项式似然，我们使用\(μ=\nu_ilog(1+exp(o_μ))\)和\(α=log(1+exp(o_α))/\sqrt{\nu_i}\)，其中\(o_μ\)，\(o_α\)是这些参数的网络输出。注意，虽然对于实值数据，可以在预处理步骤中对输入进行缩放，但这对于计数分布是不可能的。选择一个合适的比例因子本身可能很有挑战性（尤其是在数据缺失或内部方差较大的情况下）。然而，正如我们在实验中所做的那样，按平均值\(\nu_i=1+\frac{1}{t_0}\sum_{t=1}^{t_0}z_{i,t}\)缩放是一种在实践中效果良好的启发式方法。

其次，由于数据的不平衡性，随机挑选训练实例的随机优化过程会非常不频繁地访问具有大规模的少量时间序列，这导致这些时间序列的拟合不足。为了抵消这种影响，我们在训练过程中对示例进行非均匀采样。特别是，在我们的加权采样方案中，从标度为\(\nu_i\)的示例中选择窗口的概率与\(\nu_i\)成比例。

3.4 特征

协变量\(x_{i,t}\)可以是与项目相关的、与时间相关的或两者都有。2它们可以用于向模型提供关于项目或时间点（例如一年中的星期）的附加信息。它们还可以用于包括预期影响结果的协变量（例如，需求预测设置中的价格或促销状态），只要特征值也在预测范围内可用。在所有实验中，我们都使用“年龄”特征，即到该时间序列中第一次观测的距离。我们还为每小时数据添加了星期几和一天中的小时，为每周数据添加了一周，为每月数据添加了年中的月份。3此外，我们还包括了一个单一分类项目特征，通过模型学习嵌入。在零售需求预测数据集中，商品特征对应于（粗略的）产品类别（例如“服装”），而在较小的数据集中，它对应于商品的身份，允许模型学习特定商品的行为。我们将所有协变量标准化为零均值和单位方差。

4. 应用和实验

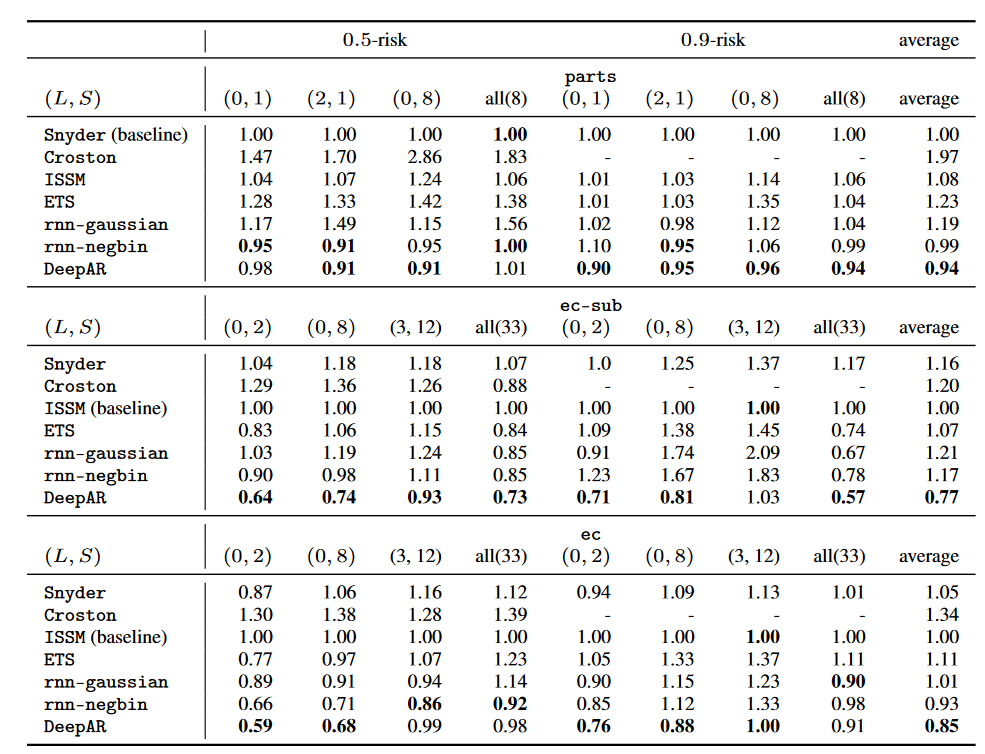
表1：相对于先前公布的最强方法（基线）的准确度指标。最佳结果用粗体标记（越低越好）。

5. 结论

我们已经证明，在各种数据集上，基于现代深度学习技术的预测方法可以大大提高预测精度，而不是现有的预测方法。我们提出的DeepAR模型有效地从相关的时间序列中学习全局模型，通过重新缩放和基于序列数据的大小采样处理广泛变化的尺度，生成高精度的校准概率预测，并能够从数据中学习复杂的模式，如季节性和不确定性随时间的增长。有趣的是，该方法在各种数据集上几乎不进行超参数调整，并且适用于仅包含几百个时间序列的中型数据集。

阅读总结：

该论文的主要工作如下：

1. 多序列概率预测DeepAR模型
2. 针对计数类数据使用负二项类概率分布
3. 引入缩放因子
4. 基于缩放因子的加权采样