点分类任务
Cora dataset(数据集描述:Yang et al. (2016))
- 论文引用数据集,每一个点有1433维向量
- 最终要对每个点进行7分类任务(每个类别只有20个点有标注)
# 点分类任务
import torch.nn
from torch import nn
from torch.nn import Linear
from torch_geometric.datasets import Planetoid #下载数据集用的
from torch_geometric.nn import GCNConv
from torch_geometric.transforms import NormalizeFeatures
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
import torch.nn.functional as F
# 导入了 Planetoid 数据集类和 NormalizeFeatures 转换。
# Planetoid 用于下载和加载常用的图数据集,而 NormalizeFeatures 用于规范化节点特征。
# 创建一个 Planetoid 数据集对象,指定了数据集的存储路径 root 和名称 Cora,同时应用了特征规范化的转换。
dataset = Planetoid(root='data/Planetoid', name='Cora', transform=NormalizeFeatures())#transform预处理
# 这部分代码用于打印有关数据集的基本信息,包括数据集的名称、图的数量、节点特征的数量以及类别的数量。
print()
print(f'Dataset: {dataset}:')
print('======================')
print(f'Number of graphs: {len(dataset)}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')
# 获取数据集中的第一个图对象,存储在变量 data 中。
data = dataset[0] # Get the first graph object.
print()
print(data)
print('===========================================================================================================')
# Gather some statistics about the graph.
print(f'Number of nodes: {data.num_nodes}') # 打印节点数量
print(f'Number of edges: {data.num_edges}') # 边的数量
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}') # 平均节点的度,即每个节点平均连接的边数
print(f'Number of training nodes: {data.train_mask.sum()}') # 训练节点数量,表示用于训练的节点数。
# b = data.train_mask.sum()
# print(b.item())
print(f'Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}') # 训练节点标签率,表示在训练集中有标签的节点占总节点数的比例。
print(f'Has isolated nodes: {data.has_isolated_nodes()}') # 是否存在孤立节点,即没有连接到其他节点的节点。
print(f'Has self-loops: {data.has_self_loops()}') # 是否存在自环边,即连接到自己的边。
print(f'Is undirected: {data.is_undirected()}') # 图是否是无向图,如果是无向图,则边没有方向性。
# val_mask和test_mask分别表示这个点需要被用到哪个数据集中
# 可视化函数:用于可视化节点特征的降维表示。
"""
当处理高维数据时,很难直观地理解数据的结构和模式。为了解决这个问题,降维技术可以帮助我们将高维数据映射到低维空间,
从而使数据更容易可视化和理解。T-SNE(t-distributed Stochastic Neighbor Embedding)是一种常用的降维方法,
通常用于可视化高维数据。
"""
# 定义了一个可视化函数 visualize(h, color),用于可视化节点特征的降维表示。
def visualize(h, color):
# 将节点特征h转换为numpy数组,并运用t-SNE算法,将高维特征映射到二维平面,并将结果存储在z中
z = TSNE(n_components=2).fit_transform(h.detach().cpu().numpy())
# 指定可视化图形窗口为10x10
plt.figure(figsize=(10, 10))
# 禁用可视化图中的x轴和y轴刻度标签
plt.xticks([])
plt.yticks([])
# z[:, 0]和z[:, 1]:这部分代码从降维后的z中提取出二维坐标,分别表示x轴和y轴上的位置。
# s = 70:这个参数指定了绘制的点的大小,s为点的大小,这里设置为70。
# c = color:这个参数指定了每个点的颜色,color是一个与节点相关的颜色信息,通常用于区分不同的节点类别或属性。
# cmap = "Set2":这个参数指定了使用的颜色映射,用于将节点的颜色与其属性关联起来。"Set2"是一个常用的颜色映射。
plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="Set2")
plt.show()
# 演示直接用传统的全连接层会怎么样?
# 自定义多层感知器(MLP)模型,用于图分类任务
class MLP(torch.nn.Module): # MLP类继承自torch.nn.Module,这是PyTorch中构建神经网络模型的基类。
def __init__(self, hidden_channels):
super().__init__()
torch.manual_seed(12345) # 这一行设置了随机种子,以确保模型的可重复性。
# MLP的第一层线性变换(全连接层),它将输入特征的维度dataset.num_features转换为hidden_channels维度。
# 这是一个线性层,用于学习输入特征的映射。
self.lin1 = Linear(dataset.num_features, hidden_channels)
# 这是MLP的第二层线性变换(全连接层),它将hidden_channels维度的特征映射到dataset.num_classes维度,
# 这是图分类任务的类别数量
self.lin2 = Linear(hidden_channels, dataset.num_classes)
# 前向传播
def forward(self, x):
# 将输入特征x传递给第一层线性变换self.lin1,这会将输入特征映射到hidden_channels维度。
x = self.lin1(x)
# 对输出应用ReLU激活函数,即对所有负值部分置零,引入非线性。
x = x.relu()
# 使用dropout随机丢弃一部分神经元,以防止过拟合。p=0.5表示每个神经元有50%的概率被丢弃。
x = F.dropout(x, p=0.5, training=self.training)
# 将特征传递给第二层线性变换,self.lin2,将特征映射到dataset.num_classes维度,这是图分类任务的输出维度。
x = self.lin2(x)
return x
# model = MLP(hidden_channels=16)
# print(model)
# 通过传统方式训练模型
model = MLP(hidden_channels=16)
criterion = torch.nn.CrossEntropyLoss() # 测量模型的预测输出与实际标签之间的差异
optimizer = torch.optim.Adam(model.parameters(), lr=1e-2, weight_decay=5e-4) # weight_decay参数用于L2正则化,有助于防止过拟合。
def train():
model.train()
optimizer.zero_grad()
out = model(data.x)
# 计算损失,只计算具有标签的训练节点的损失。
loss = criterion(out[data.train_mask], data.y[data.train_mask])
loss.backward()
optimizer.step()
return loss
def test():
model.eval()
out = model(data.x)
# 计算每个节点的预测类别,取概率最高的类别。
"""
- out是模型在测试数据上的输出,通常是一个举证,其中每一行对应一个样本(节点),
每一列对应一个类别。每个元素表示模型对该样本属于某个类别的概率。
- argmax(dim=1)是一个张量操作,它的作用是沿着维度1(列的维度)找到每行中的最大值所在的列的索引。
这就是在模型的输出中找到每个样本的预测类别。
"""
pred = out.argmax(dim=1)
# 通过比较预测类别和实际类别,确定测试集中哪些节点被正确分类。
test_correct = pred[data.test_mask] == data.y[data.test_mask]
# 计算测试准确率,即被正确分类的节点数除以测试集中的节点总数。
test_acc = int(test_correct.sum()) / int(data.test_mask.sum())
return test_acc
for epoch in range(1, 201):
loss = train()
print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')
# 准确率计算
test_acc = test()
print(f'Test Accuracy: {test_acc:.4f}')
# 将全连接层替换成GCN层
class GCN(nn.Module):
def __init__(self, hidden_channels):
super().__init__()
# 设置随机种子,以确保模型的可重复性。
torch.manual_seed(1234567)
self.conv1 = GCNConv(dataset.num_features, hidden_channels)
self.conv2 = GCNConv(hidden_channels, dataset.num_classes)
def forward(self, x, edge_index):
x = self.conv1(x, edge_index)
x = x.relu() # 对输出应用ReLU激活函数,即对所有负值部分置零,引入非线性性质。
# training=self.training表示只在模型训练时应用dropout
"""
- 在深度学习中,Dropout是一种正则化技术,用于减少模型的过拟合,提高模型的泛化能力。
它的核心思想是在每次前向传播中随机丢弃一部分神经元(节点)的输出,从而降低神经网络的复杂性,
强制模型不过度依赖某些特定神经元,提高模型的鲁棒性。
- training=self.training:这是一个布尔值,通常用来控制dropout在训练和测试时的行为。
当 self.training 为 True 时,表示模型处于训练模式,此时dropout会生效;
当 self.training 为 False 时,表示模型处于测试或推理模式,dropout不会生效。
- 在训练过程中,dropout会随机将输入张量 x 中的一部分元素设置为零,即将它们丢弃。
这样可以防止模型对特定的输入特征过于敏感,有助于减少过拟合。
在测试或推理时,dropout不会生效,因此模型的预测是稳定的。
"""
x = F.dropout(x, p=0.5, training=self.training)
x = self.conv2(x, edge_index)
return x
model = GCN(hidden_channels=16)
# print(model)
# 可视化的时候由于输出是7为向量,所以降维成2维进行展示
# model = GCN(hidden_channels=16)
# model.eval()
# out = model(data.x, data.edge_index)
# visualize(out, color=data.y)
# 训练GCN模型
model = GCN(hidden_channels=16)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-2, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()
def train():
model.train()
optimizer.zero_grad()
out = model(data.x, data.edge_index)
loss = criterion(out[data.train_mask], data.y[data.train_mask])
loss.backward()
optimizer.step()
return loss
def test():
model.eval()
out = model(data.x, data.edge_index)
pred = out.argmax(dim=1)
test_correct = pred[data.test_mask] == data.y[data.test_mask]
test_acc = int(test_correct.sum()) / int(data.test_mask.sum())
return test_acc
for epoch in range(1, 101):
loss = train()
print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')
# 准确率计算
test_acc = test()
print(f'Test Accuracy: {test_acc:.4f}')
model.eval()
out = model(data.x, data.edge_index)
visualize(out, color=data.y)
全连接层训练后的结果
Epoch: 001, Loss: 1.9615
Epoch: 002, Loss: 1.9557
Epoch: 003, Loss: 1.9505
Epoch: 004, Loss: 1.9423
Epoch: 005, Loss: 1.9327
Epoch: 006, Loss: 1.9279
Epoch: 007, Loss: 1.9144
Epoch: 008, Loss: 1.9087
Epoch: 009, Loss: 1.9023
Epoch: 010, Loss: 1.8893
Epoch: 011, Loss: 1.8776
Epoch: 012, Loss: 1.8594
Epoch: 013, Loss: 1.8457
Epoch: 014, Loss: 1.8365
Epoch: 015, Loss: 1.8280
Epoch: 016, Loss: 1.7965
Epoch: 017, Loss: 1.7984
Epoch: 018, Loss: 1.7832
Epoch: 019, Loss: 1.7495
Epoch: 020, Loss: 1.7441
Epoch: 021, Loss: 1.7188
Epoch: 022, Loss: 1.7124
Epoch: 023, Loss: 1.6785
Epoch: 024, Loss: 1.6660
Epoch: 025, Loss: 1.6119
Epoch: 026, Loss: 1.6236
Epoch: 027, Loss: 1.5827
Epoch: 028, Loss: 1.5784
Epoch: 029, Loss: 1.5524
Epoch: 030, Loss: 1.5020
Epoch: 031, Loss: 1.5065
Epoch: 032, Loss: 1.4742
Epoch: 033, Loss: 1.4581
Epoch: 034, Loss: 1.4246
Epoch: 035, Loss: 1.4131
Epoch: 036, Loss: 1.4112
Epoch: 037, Loss: 1.3923
Epoch: 038, Loss: 1.3055
Epoch: 039, Loss: 1.2982
Epoch: 040, Loss: 1.2543
Epoch: 041, Loss: 1.2244
Epoch: 042, Loss: 1.2331
Epoch: 043, Loss: 1.1984
Epoch: 044, Loss: 1.1796
Epoch: 045, Loss: 1.1093
Epoch: 046, Loss: 1.1284
Epoch: 047, Loss: 1.1229
Epoch: 048, Loss: 1.0383
Epoch: 049, Loss: 1.0439
Epoch: 050, Loss: 1.0563
Epoch: 051, Loss: 0.9893
Epoch: 052, Loss: 1.0508
Epoch: 053, Loss: 0.9343
Epoch: 054, Loss: 0.9639
Epoch: 055, Loss: 0.8929
Epoch: 056, Loss: 0.8705
Epoch: 057, Loss: 0.9176
Epoch: 058, Loss: 0.9239
Epoch: 059, Loss: 0.8641
Epoch: 060, Loss: 0.8578
Epoch: 061, Loss: 0.7908
Epoch: 062, Loss: 0.7856
Epoch: 063, Loss: 0.7683
Epoch: 064, Loss: 0.7816
Epoch: 065, Loss: 0.7356
Epoch: 066, Loss: 0.6951
Epoch: 067, Loss: 0.7300
Epoch: 068, Loss: 0.6939
Epoch: 069, Loss: 0.7550
Epoch: 070, Loss: 0.6864
Epoch: 071, Loss: 0.7094
Epoch: 072, Loss: 0.7238
Epoch: 073, Loss: 0.7150
Epoch: 074, Loss: 0.6191
Epoch: 075, Loss: 0.6770
Epoch: 076, Loss: 0.6487
Epoch: 077, Loss: 0.6258
Epoch: 078, Loss: 0.5821
Epoch: 079, Loss: 0.5637
Epoch: 080, Loss: 0.6368
Epoch: 081, Loss: 0.6333
Epoch: 082, Loss: 0.6434
Epoch: 083, Loss: 0.5974
Epoch: 084, Loss: 0.6176
Epoch: 085, Loss: 0.5972
Epoch: 086, Loss: 0.4690
Epoch: 087, Loss: 0.6362
Epoch: 088, Loss: 0.6118
Epoch: 089, Loss: 0.5248
Epoch: 090, Loss: 0.5520
Epoch: 091, Loss: 0.6130
Epoch: 092, Loss: 0.5361
Epoch: 093, Loss: 0.5594
Epoch: 094, Loss: 0.5049
Epoch: 095, Loss: 0.5043
Epoch: 096, Loss: 0.5235
Epoch: 097, Loss: 0.5451
Epoch: 098, Loss: 0.5329
Epoch: 099, Loss: 0.5008
Epoch: 100, Loss: 0.5350
Epoch: 101, Loss: 0.5343
Epoch: 102, Loss: 0.5138
Epoch: 103, Loss: 0.5377
Epoch: 104, Loss: 0.5353
Epoch: 105, Loss: 0.5176
Epoch: 106, Loss: 0.5229
Epoch: 107, Loss: 0.4558
Epoch: 108, Loss: 0.4883
Epoch: 109, Loss: 0.4659
Epoch: 110, Loss: 0.4908
Epoch: 111, Loss: 0.4966
Epoch: 112, Loss: 0.4725
Epoch: 113, Loss: 0.4787
Epoch: 114, Loss: 0.4390
Epoch: 115, Loss: 0.4199
Epoch: 116, Loss: 0.4810
Epoch: 117, Loss: 0.4484
Epoch: 118, Loss: 0.5080
Epoch: 119, Loss: 0.4241
Epoch: 120, Loss: 0.4745
Epoch: 121, Loss: 0.4651
Epoch: 122, Loss: 0.4652
Epoch: 123, Loss: 0.5580
Epoch: 124, Loss: 0.4861
Epoch: 125, Loss: 0.4405
Epoch: 126, Loss: 0.4292
Epoch: 127, Loss: 0.4409
Epoch: 128, Loss: 0.3575
Epoch: 129, Loss: 0.4468
Epoch: 130, Loss: 0.4603
Epoch: 131, Loss: 0.4108
Epoch: 132, Loss: 0.4601
Epoch: 133, Loss: 0.4258
Epoch: 134, Loss: 0.3852
Epoch: 135, Loss: 0.4028
Epoch: 136, Loss: 0.4245
Epoch: 137, Loss: 0.4300
Epoch: 138, Loss: 0.4693
Epoch: 139, Loss: 0.4314
Epoch: 140, Loss: 0.4031
Epoch: 141, Loss: 0.4290
Epoch: 142, Loss: 0.4110
Epoch: 143, Loss: 0.3863
Epoch: 144, Loss: 0.4215
Epoch: 145, Loss: 0.4519
Epoch: 146, Loss: 0.3940
Epoch: 147, Loss: 0.4429
Epoch: 148, Loss: 0.3527
Epoch: 149, Loss: 0.4390
Epoch: 150, Loss: 0.4212
Epoch: 151, Loss: 0.4128
Epoch: 152, Loss: 0.3779
Epoch: 153, Loss: 0.4801
Epoch: 154, Loss: 0.4130
Epoch: 155, Loss: 0.3962
Epoch: 156, Loss: 0.4262
Epoch: 157, Loss: 0.4210
Epoch: 158, Loss: 0.4081
Epoch: 159, Loss: 0.4066
Epoch: 160, Loss: 0.3782
Epoch: 161, Loss: 0.3836
Epoch: 162, Loss: 0.4172
Epoch: 163, Loss: 0.3993
Epoch: 164, Loss: 0.4477
Epoch: 165, Loss: 0.3714
Epoch: 166, Loss: 0.3610
Epoch: 167, Loss: 0.4546
Epoch: 168, Loss: 0.4387
Epoch: 169, Loss: 0.3793
Epoch: 170, Loss: 0.3704
Epoch: 171, Loss: 0.4286
Epoch: 172, Loss: 0.4131
Epoch: 173, Loss: 0.3795
Epoch: 174, Loss: 0.4230
Epoch: 175, Loss: 0.4139
Epoch: 176, Loss: 0.3586
Epoch: 177, Loss: 0.3588
Epoch: 178, Loss: 0.3911
Epoch: 179, Loss: 0.3810
Epoch: 180, Loss: 0.4203
Epoch: 181, Loss: 0.3583
Epoch: 182, Loss: 0.3690
Epoch: 183, Loss: 0.4025
Epoch: 184, Loss: 0.3920
Epoch: 185, Loss: 0.4369
Epoch: 186, Loss: 0.4317
Epoch: 187, Loss: 0.4911
Epoch: 188, Loss: 0.3369
Epoch: 189, Loss: 0.4945
Epoch: 190, Loss: 0.3912
Epoch: 191, Loss: 0.3824
Epoch: 192, Loss: 0.3479
Epoch: 193, Loss: 0.3798
Epoch: 194, Loss: 0.3799
Epoch: 195, Loss: 0.4015
Epoch: 196, Loss: 0.3615
Epoch: 197, Loss: 0.3985
Epoch: 198, Loss: 0.4664
Epoch: 199, Loss: 0.3714
Epoch: 200, Loss: 0.3810
Test Accuracy: 0.5900
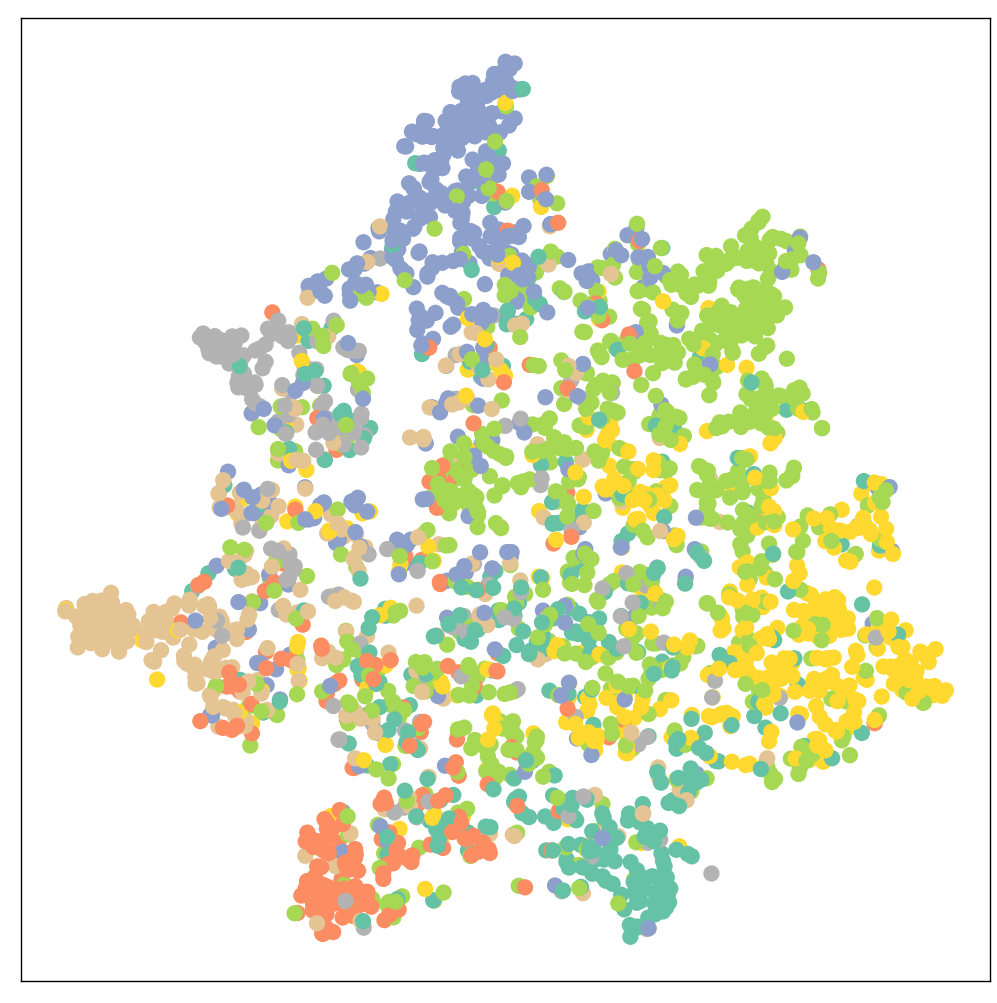
GCN替代全连接层后的训练结果
Epoch: 001, Loss: 1.9463
Epoch: 002, Loss: 1.9409
Epoch: 003, Loss: 1.9343
Epoch: 004, Loss: 1.9275
Epoch: 005, Loss: 1.9181
Epoch: 006, Loss: 1.9086
Epoch: 007, Loss: 1.9015
Epoch: 008, Loss: 1.8933
Epoch: 009, Loss: 1.8808
Epoch: 010, Loss: 1.8685
Epoch: 011, Loss: 1.8598
Epoch: 012, Loss: 1.8482
Epoch: 013, Loss: 1.8290
Epoch: 014, Loss: 1.8233
Epoch: 015, Loss: 1.8057
Epoch: 016, Loss: 1.7966
Epoch: 017, Loss: 1.7825
Epoch: 018, Loss: 1.7617
Epoch: 019, Loss: 1.7491
Epoch: 020, Loss: 1.7310
Epoch: 021, Loss: 1.7147
Epoch: 022, Loss: 1.7056
Epoch: 023, Loss: 1.6954
Epoch: 024, Loss: 1.6697
Epoch: 025, Loss: 1.6538
Epoch: 026, Loss: 1.6312
Epoch: 027, Loss: 1.6161
Epoch: 028, Loss: 1.5899
Epoch: 029, Loss: 1.5711
Epoch: 030, Loss: 1.5576
Epoch: 031, Loss: 1.5393
Epoch: 032, Loss: 1.5137
Epoch: 033, Loss: 1.4948
Epoch: 034, Loss: 1.4913
Epoch: 035, Loss: 1.4698
Epoch: 036, Loss: 1.3998
Epoch: 037, Loss: 1.4041
Epoch: 038, Loss: 1.3761
Epoch: 039, Loss: 1.3631
Epoch: 040, Loss: 1.3258
Epoch: 041, Loss: 1.3030
Epoch: 042, Loss: 1.3119
Epoch: 043, Loss: 1.2519
Epoch: 044, Loss: 1.2530
Epoch: 045, Loss: 1.2492
Epoch: 046, Loss: 1.2205
Epoch: 047, Loss: 1.2037
Epoch: 048, Loss: 1.1571
Epoch: 049, Loss: 1.1700
Epoch: 050, Loss: 1.1296
Epoch: 051, Loss: 1.0860
Epoch: 052, Loss: 1.1080
Epoch: 053, Loss: 1.0564
Epoch: 054, Loss: 1.0157
Epoch: 055, Loss: 1.0362
Epoch: 056, Loss: 1.0328
Epoch: 057, Loss: 1.0058
Epoch: 058, Loss: 0.9865
Epoch: 059, Loss: 0.9667
Epoch: 060, Loss: 0.9741
Epoch: 061, Loss: 0.9769
Epoch: 062, Loss: 0.9122
Epoch: 063, Loss: 0.8993
Epoch: 064, Loss: 0.8769
Epoch: 065, Loss: 0.8575
Epoch: 066, Loss: 0.8897
Epoch: 067, Loss: 0.8312
Epoch: 068, Loss: 0.8262
Epoch: 069, Loss: 0.8511
Epoch: 070, Loss: 0.7711
Epoch: 071, Loss: 0.8012
Epoch: 072, Loss: 0.7529
Epoch: 073, Loss: 0.7525
Epoch: 074, Loss: 0.7689
Epoch: 075, Loss: 0.7553
Epoch: 076, Loss: 0.7032
Epoch: 077, Loss: 0.7326
Epoch: 078, Loss: 0.7122
Epoch: 079, Loss: 0.7090
Epoch: 080, Loss: 0.6755
Epoch: 081, Loss: 0.6666
Epoch: 082, Loss: 0.6679
Epoch: 083, Loss: 0.7037
Epoch: 084, Loss: 0.6752
Epoch: 085, Loss: 0.6266
Epoch: 086, Loss: 0.6564
Epoch: 087, Loss: 0.6266
Epoch: 088, Loss: 0.6411
Epoch: 089, Loss: 0.6226
Epoch: 090, Loss: 0.6535
Epoch: 091, Loss: 0.6317
Epoch: 092, Loss: 0.5741
Epoch: 093, Loss: 0.5572
Epoch: 094, Loss: 0.5710
Epoch: 095, Loss: 0.5816
Epoch: 096, Loss: 0.5745
Epoch: 097, Loss: 0.5547
Epoch: 098, Loss: 0.5989
Epoch: 099, Loss: 0.6021
Epoch: 100, Loss: 0.5799
Test Accuracy: 0. 8150
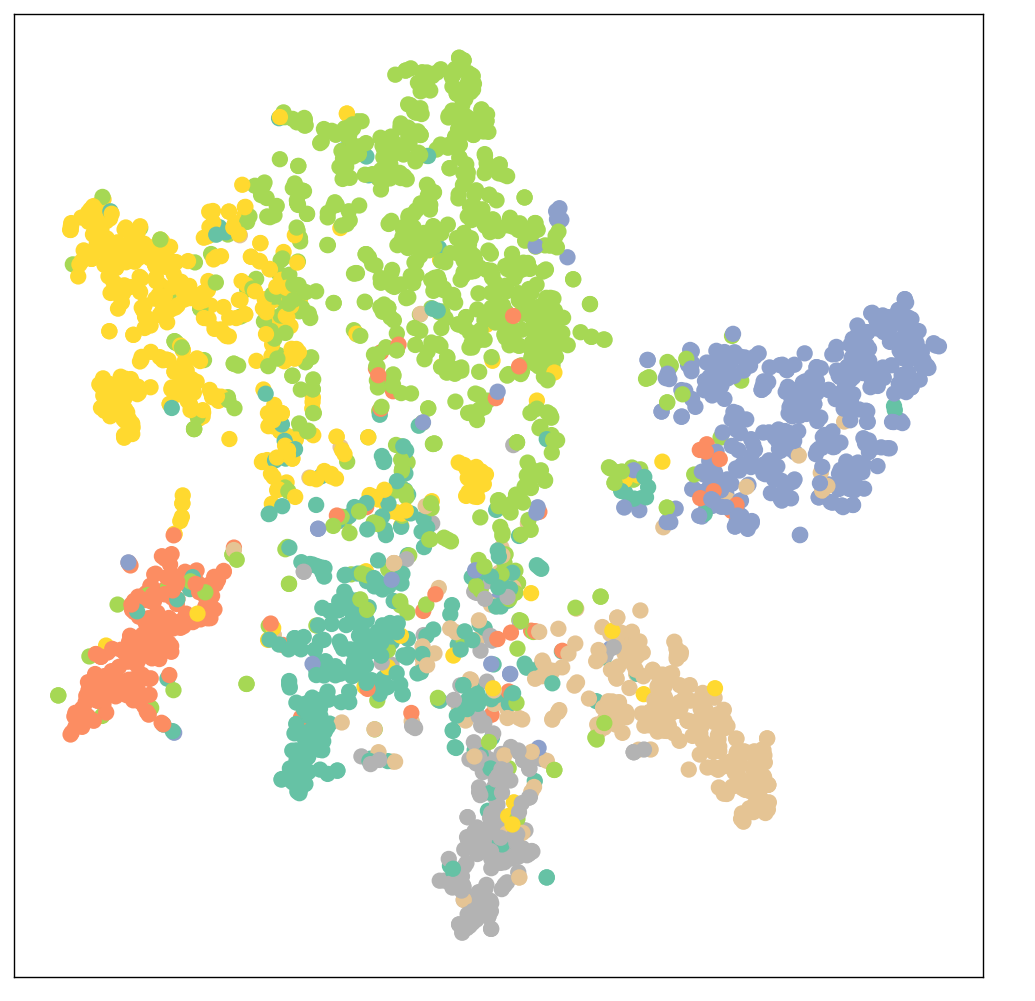 标签:实战,Loss,模型,分类,test,Epoch,print,data,self
From: https://www.cnblogs.com/codingbao/p/17763308.html
标签:实战,Loss,模型,分类,test,Epoch,print,data,self
From: https://www.cnblogs.com/codingbao/p/17763308.html