T1 树上的数
题解
比上一次好一些的第一题
不过我还是没做出来
一眼树形 \(dp\)
不过状态设计和转移不是很好列
容易想到对于子树枚举,记录 \(f_{i,j}\) 表示 \(i\) 的子树空出了 \(j\) 个点时的方案数
对于每一个节点的初始状态都是 \(f_{i,0} = n-dep_i \ \ \ f_{i,1} = 1\)
为什么呢?
对于第二个状态很好理解,选一个只有一种情况
对于第一个则是因为会影响这个点做选择的只有从它到根节点这一段路径上的节点,自己想想就能明白
说完了初始状态说转移
对于子树的合并明显有 \(f'_{u,i+j}+=f_{u,i}\times f_{v,j}\) 其中的 \(f'\) 为临时数组,因为这个遍历过程中 \(f\) 不能被更改
这个转移式的意思就是对于当前答案与子树答案相乘,因为是满足乘法原理
分别在当前统计过的位置选 \(i\) 个和子树内选 \(j\) 个位置空出来
统计完空位后别忘了用组合数统计当前节点需要选出来的位置的方案数
#include<bits/stdc++.h>
#define N 5010
#define mod 998244353
using namespace std;
int n,cnt,b[N],f[N][N],siz[N],tmp[N],fac[N],inv[N],dep[N];
vector<int>g[N];
int ksm(int x,int y){
int res = 1;
while(y){
if(y&1) res = 1ll*res*x%mod;
x = 1ll*x*x%mod;
y>>=1;
}
return res;
}
int C(int x,int y){
if(x<y) return 1;
return 1ll*fac[x]*inv[y]%mod*inv[x-y]%mod;
}
void dfs(int u){
siz[u] = f[u][1] = 1;
f[u][0] = n-dep[u];
for(int v : g[u]){
dfs(v);
for(int i = 0;i<=siz[u];i++)
for(int j = 0;j<=siz[v];j++)
tmp[i+j] = (tmp[i+j]+1ll*f[u][i]*f[v][j]%mod)%mod;
siz[u]+=siz[v];
for(int i = 0;i<=siz[u];i++){
f[u][i] = tmp[i];
tmp[i] = 0;
}
}
for(int i = b[u];i<=siz[u];i++)
tmp[i-b[u]] = 1ll*f[u][i]*C(i,b[u])%mod;
for(int i = 0;i<=siz[u];i++){
f[u][i] = tmp[i];
tmp[i] = 0;
}
}
int main(){
freopen("treei.in","r",stdin);
freopen("treei.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n;
fac[0] = 1;
for(int i = 1;i<=n;i++) fac[i] = 1ll*fac[i-1]*i%mod;
inv[n] = ksm(fac[n],mod-2);
for(int i = n-1;i>=0;i--) inv[i] = 1ll*inv[i+1]*(i+1)%mod;
dep[1] = 1;
for(int i = 2;i<=n;i++){
int x;cin>>x;
g[x].push_back(i);
dep[i] = dep[x]+1;
}
for(int i = 1;i<=n;i++)
cin>>b[i];
dfs(1);
cout<<f[1][0];
return 0;
}
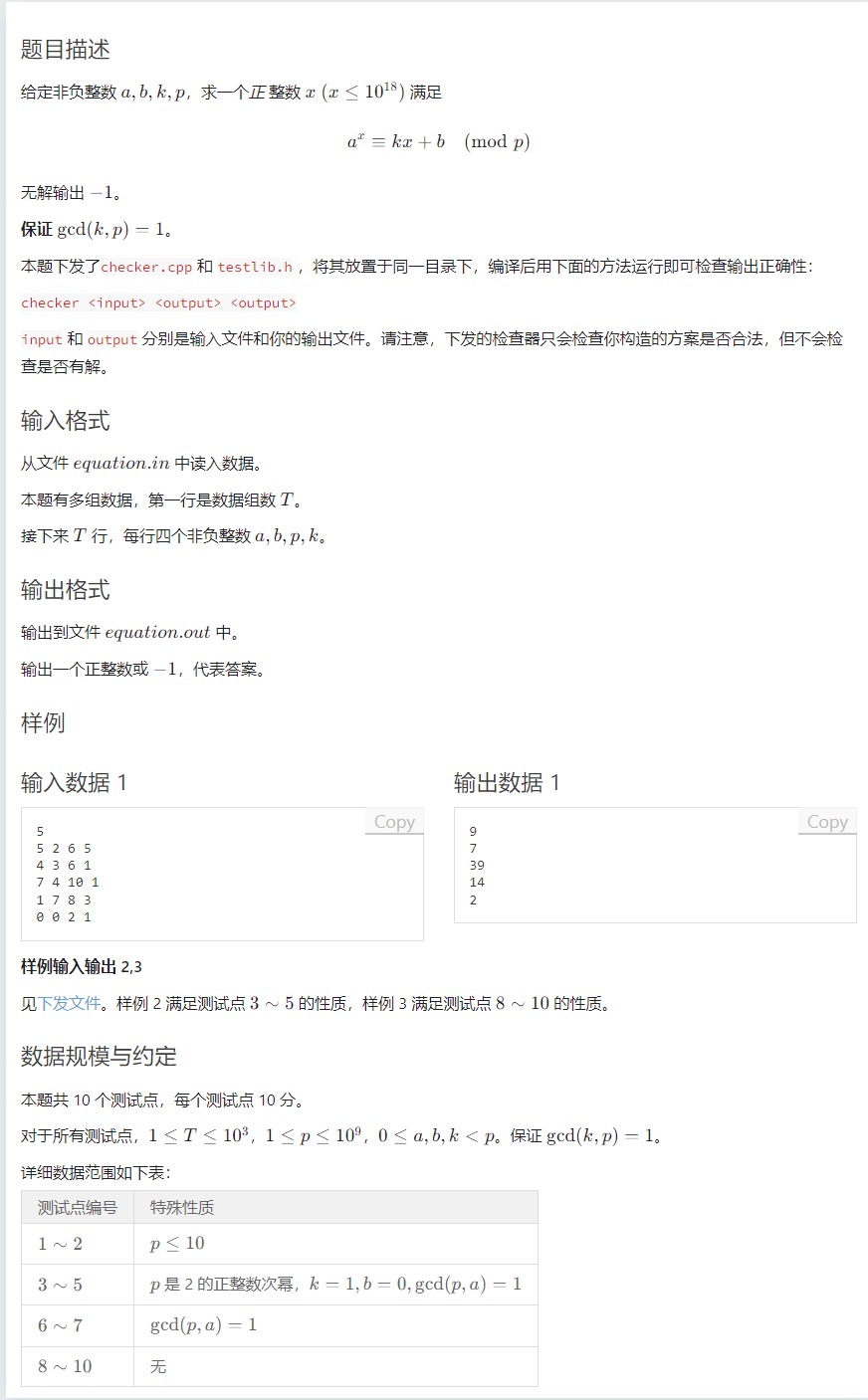
T2 解方程
题解
一道说起来挺麻烦的数学题
当 \(\gcd(a,p) = 1\) 时,假设已经知道 \(U\),使得方程的一个解为 \(k x+b \equiv a^{x} \equiv U(\bmod p)\)
此时,\(k x+b \equiv U\) \((\bmod p)\) 相当于 \(x \equiv C_{1}(\bmod p)\left(C_{1}\right.\) 是一个常数,因为 \(\gcd(k,p)=1\),所以 \(C_{1}\) 总是存在的 \()\)
而 \(a^{x} \equiv U(\bmod p)\),相当于 \(x \equiv C_{2}(\bmod \varphi(p))\) 。如果希望最终的 \(x\) 存在,就需要 \(C_{1} \equiv C_{2}(\bmod \gcd(p,\varphi(p)))\)
令 \(q = \gcd(p,\varphi(p))\)
假设已经知道 \(x_{0}\) 满足 \(k x_{0}+b \equiv a^{x_{0}}(\bmod q)\),考虑令 \(U=\left(k x_{0}+b\right) \bmod p\)
此时,上述式子中,\(C_{1}=x_{0} \bmod p,C_{2}=x_{0} \bmod \varphi(p)\),满足要求
因此,只要知道模数为 \(q\) 时的解 \(x_{0}\),通过扩展中国剩余定理合并两个同余方程,就可以得到模数为 \(p\) 时的解
故最终算法为不停递归,每次令 \(p = \gcd(p,\varphi(p))\),当 \(p=1\) 时,\(x=1\) 总是合法解,然后倒推出最初要求的解
从这里也看出,不可能无解
计算 \(\varphi\) 需要对 \(p\) 分解质因数,瓶颈也在这里,后面的递归,每次递归 \(p\) 至少减半,不影响时间复杂度
最终时间复杂度 \(O(T \sqrt{p})\) 。
由此也可以看出,对于测试点 \(3 \sim 5,p = 2^{k}\),设 \(p=2^{k-1}\) 时的解为 \(x_{0}\),那么新解只会是 \(x_{0}\) 或者 \(x_{0}+2^{k-1}\)
前面只是讨论了测试点 \(3\sim 5\) 的情况,不过我们可以推广到整个范围
当 \(\gcd(a,p) \neq 1\) 时,我们需要给 \(x\) 一个下界,因为拓展欧拉定理要求 \(x \geq \varphi(p)\)
只需要在解同余方程时强制要 求解 \(\geq 10^{9}\) 即可
时间复杂度 \(O(T \sqrt{p})\) 。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int cnt,pri[50];
void exgcd(int a,int b,int &x,int &y){
if(!b){
x = 1,y = 0;
return ;
}
exgcd(b,a%b,y,x);
y-=a/b*x;
}
int ksm(int x,int y,int p){
int res = 1;
while(y){
if(y&1) res = res*x%p;
x = x*x%p;
y>>=1;
}
return res;
}
int inv(int x,int p){
int a,b;
exgcd(x,p,a,b);
a = (a%p+p)%p;
return a;
}
int gcd(int a,int b){
return !b?a:gcd(b,a%b);
}
int solve(int a,int b,int k,int p){
if(p==1) return 1e9;
int phi = p;
for(int i = 1;i<=cnt;i++)
if(p%pri[i]==0) phi = phi/pri[i]*(pri[i]-1);
int g = gcd(p,phi),tmp = solve(a,b,k,g);
int v = (ksm(a,tmp,p)-b+p)%p*inv(k,p)%p,A,B;
exgcd(phi,p,A,B);
A = (A%p+p)%p;
A*=(v-tmp)/g;
A = (A%p+p)%p;
int x = phi*A+tmp;
int lcm = p/g*phi;
x = (x%lcm+lcm)%lcm;
if(x<1e9) x+=lcm;
return x;
}
signed main(){
freopen("equation.in","r",stdin);
freopen("equation.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;cin>>T;
while(T--){
int a,b,p,k;
cin>>a>>b>>p>>k;
cnt = 0;
int tmp = p;
for(int i = 2;i*i<=tmp;i++){
if(tmp%i==0){
while(tmp%i==0) tmp/=i;
pri[++cnt] = i;
}
}
if(tmp>1) pri[++cnt] = tmp;
cout<<solve(a,b,k,p)<<"\n";
}
return 0;
}
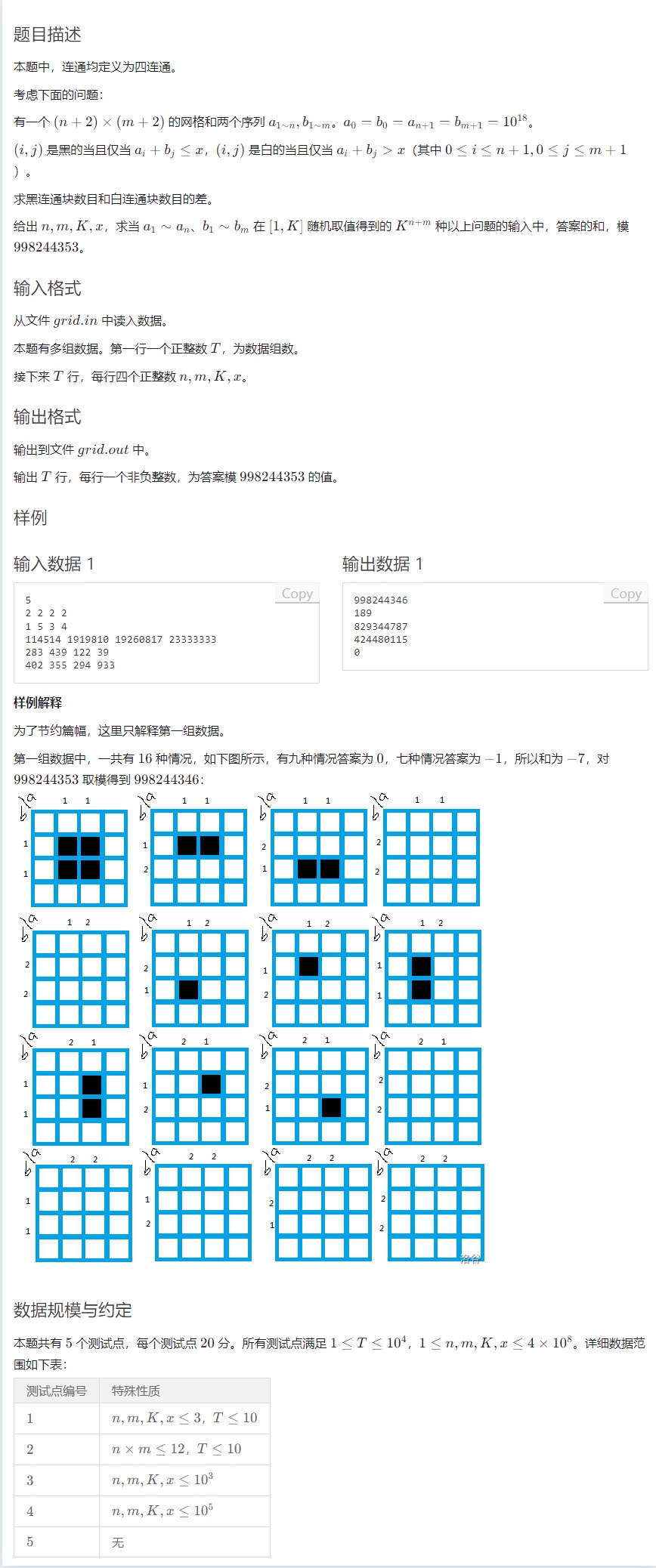
T3 网络
题解
我不会那就直接贴题解
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define yu (998244353)
inline void add(ll &x,ll y){x+=y;if(x>=yu)x-=yu;return;}
#define N 100010
ll n,m,k,x;
ll sum[N];
inline ll ksm(ll x,ll y=yu-2){
ll an=1;for(;y;y>>=1){
if(y&1)an=an*x%yu;
x=x*x%yu;
}return an;
}
inline ll gtd(){
/*ll an=0;for(int i=1;i<=min(k,x);i++){
add(an,min(k,x-i));
}*/if(x<=k+1){
return x*(x-1)/2%yu;
}return (k*(x-k-1)+(k+(x-k))*(2*k-x+1)/2)%yu;
}
inline ll gtf(ll x,ll y){x--;return (y*(2*y+1)%yu*(y+1)%yu*ksm(6)%yu-x*(2*x+1)%yu*(x+1)%yu*ksm(6)%yu+yu)%yu;}
inline ll gtl(ll x,ll y){x--;return ((y*(y+1)/2)%yu*(y*(y+1)/2%yu)%yu-(x*(x+1)/2)%yu*(x*(x+1)/2%yu)%yu+yu)%yu;}
inline ll gt(ll l,ll r){return (2*x*gtf(l,r)%yu-(2*gtl(l,r)+gtf(l,r))%yu+yu)%yu;}
inline ll gtb(){
// for(int i=1;i<=k;i++)sum[i]=2*i-1;for(int i=1;i<=k;i++)add(sum[i],sum[i-1]);
/*ll an=0;for(int i=1;i<=min(k,x);i++){
add(an,sum[min(k,x-i)]);
}*/if(x<=k+1){
return gtf(1,x-1);
}return (gtf(k,k)*(x-k-1)+gtf(x-k,k))%yu;
}
inline ll gth(){
/*for(int i=1;i<=k;i++)sum[i]=2*i-1;for(int i=1;i<=k;i++)add(sum[i],sum[i-1]);
ll an=0;for(ll i=1;i<=min(k,x);i++){
add(an,(2*i-1)*sum[min(k,x-i)]%yu);
}*/if(x<=k+1){
return gt(1,x-1);
}return (gtf(k,k)*(x-k-1)%yu*(x-k-1)%yu+gt(x-k,k))%yu;
}
int main(){
// freopen("test1.in","r",stdin);
freopen("grid.in","r",stdin);
freopen("grid.out","w",stdout);
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
ll ti;cin>>ti;while(ti--){
cin>>n>>m>>k>>x;x=min(x,2*k);ll tem=ksm(k),sum=ksm(k,n+m);
ll ans=yu-sum;
ll an=gtd();
add(ans,an*n%yu*m%yu*sum%yu*tem%yu*tem%yu);
an=gtb();
add(ans,yu-an*((n*(m-1)+(n-1)*m)%yu)%yu*sum%yu*tem%yu*tem%yu*tem%yu);
an=gth();
if(n>1&&m>1)add(ans,an*((n-1)*(m-1)%yu)%yu*sum%yu*tem%yu*tem%yu*tem%yu*tem%yu);
cout<<ans<<'\n';
}return 0;
}
个人认为比较简单的代码
下面是题解代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 998244353;
int Power(int x, int y) {
int ret = 1;
while (y) {
if (y & 1) ret = 1ll * ret * x % mod;
x = 1ll * x * x % mod, y >>= 1;
}
return ret;
}
int S1(int l, int r) { return 1ll * (l + r) * (r - l + 1) / 2 % mod; }
int S2r(int r) { return 1ll * r * (r + 1) % mod * (2 * r + 1) % mod * (mod + 1) / 6 % mod; }
int S2(int l, int r) { return (S2r(r) - S2r(l - 1) + mod) % mod; }
int S3r(int r) { return 1ll * S1(1, r) * S1(1, r) % mod; }
int S3(int l, int r) { return (S3r(r) - S3r(l - 1) + mod) % mod; }
int main() {
freopen("grid.in", "r", stdin);
freopen("grid.out", "w", stdout);
int t;
cin >> t;
while (t--) {
int n, m, K, x, ans = 0;
cin >> n >> m >> K >> x, x = min(x, K * 2);
if (x <= K + 1) {
ans = (ans + 1ll * x * (x - 1) / 2 % mod * Power(1ll * K * K % mod, mod - 2) % mod * n %
mod * m % mod) %
mod;
ans = (ans -
1ll * S2r(x - 1) * Power(1ll * K * K % mod * K % mod, mod - 2) % mod * n % mod *
(m - 1) % mod +
mod) %
mod;
ans = (ans -
1ll * S2r(x - 1) * Power(1ll * K * K % mod * K % mod, mod - 2) % mod * (n - 1) %
mod * m % mod +
mod) %
mod;
ans = (ans + 2ll * S3r(x - 1) * Power(1ll * K * K % mod * K % mod * K % mod, mod - 2) %
mod * (n - 1) % mod * (m - 1) % mod) %
mod;
ans = (ans + 2ll * x * x % mod * S1(1, x - 1) % mod *
Power(1ll * K * K % mod * K % mod * K % mod, mod - 2) % mod * (n - 1) %
mod * (m - 1) % mod) %
mod;
ans = (ans -
4ll * x % mod * S2(1, x - 1) % mod *
Power(1ll * K * K % mod * K % mod * K % mod, mod - 2) % mod * (n - 1) % mod *
(m - 1) % mod +
mod) %
mod;
ans = (ans -
1ll * S2r(x - 1) * Power(1ll * K * K % mod * K % mod * K % mod, mod - 2) % mod *
(n - 1) % mod * (m - 1) % mod +
mod) %
mod;
} else {
ans = (ans + 1ll * S1(x - K, K - 1) * Power(1ll * K * K % mod, mod - 2) % mod * n %
mod * m % mod) %
mod;
ans = (ans + 1ll * K * (x - K) % mod * Power(1ll * K * K % mod, mod - 2) % mod * n %
mod * m % mod) %
mod;
ans = (ans -
1ll * S2(x - K, K - 1) * Power(1ll * K * K % mod * K % mod, mod - 2) % mod * n %
mod * (m - 1) % mod +
mod) %
mod;
ans = (ans -
1ll * S2(x - K, K - 1) * Power(1ll * K * K % mod * K % mod, mod - 2) % mod *
(n - 1) % mod * m % mod +
mod) %
mod;
ans = (ans -
1ll * K * K % mod * (x - K) % mod * Power(1ll * K * K % mod * K % mod, mod - 2) %
mod * n % mod * (m - 1) % mod +
mod) %
mod;
ans = (ans -
1ll * K * K % mod * (x - K) % mod * Power(1ll * K * K % mod * K % mod, mod - 2) %
mod * (n - 1) % mod * m % mod +
mod) %
mod;
ans = (ans + 2ll * S3(x - K + 1, K) *
Power(1ll * K * K % mod * K % mod * K % mod, mod - 2) % mod * (n - 1) %
mod * (m - 1) % mod) %
mod;
ans = (ans + 2ll * x * x % mod * S1(x - K + 1, K) % mod *
Power(1ll * K * K % mod * K % mod * K % mod, mod - 2) % mod * (n - 1) %
mod * (m - 1) % mod) %
mod;
ans = (ans -
4ll * x % mod * S2(x - K + 1, K) % mod *
Power(1ll * K * K % mod * K % mod * K % mod, mod - 2) % mod * (n - 1) % mod *
(m - 1) % mod +
mod) %
mod;
ans = (ans + 2ll * K * K % mod * S1(1, x - K) % mod *
Power(1ll * K * K % mod * K % mod * K % mod, mod - 2) % mod * (n - 1) %
mod * (m - 1) % mod) %
mod;
ans = (ans -
1ll * S2(x - K, K - 1) * Power(1ll * K * K % mod * K % mod * K % mod, mod - 2) %
mod * (n - 1) % mod * (m - 1) % mod +
mod) %
mod;
ans = (ans -
1ll * K * K % mod * (x - K) % mod *
Power(1ll * K * K % mod * K % mod * K % mod, mod - 2) % mod * (n - 1) % mod *
(m - 1) % mod +
mod) %
mod;
}
ans = (ans - 1 + mod) % mod;
cout << 1ll * ans * Power(K, n + m) % mod << '\n';
}
}
T4
照样不会
标签:校内,int,ll,return,231011,yu,bmod,mod From: https://www.cnblogs.com/cztq/p/17758134.html