感谢 EC 姐姐与 HMZ 姐姐对我的帮助!/qq
这是模板题这个
现在你就知道 AC 自动机干嘛用的,是用来对多个模式串匹配一个文本串的。如果是一个模式串匹配一个文本串呢?我们可以 KMP。我们回忆一下 KMP 是怎么做的,先得到模式串的失配指针 \(nxt\),\(nxt_i\) 代表如果在 \(i\) 位置失配了那么要跳到哪个位置。因此最后我们可以得到一个大概像图的一个东西,炒个例子
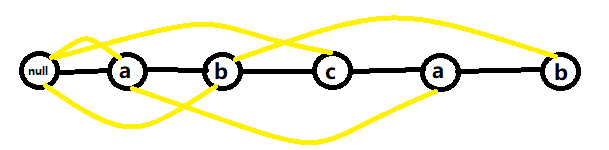
(其实所有黄边都是从右往左连的,也就是说这是一张有向图,因为 windows 画图太难受了就没画方向)
如果有一个文本串,然后我们用模式串挨个和它匹配,如果模式串第 \(j + 1\) 位和文本串第 \(i + 1\) 位失配,我们就让 \(j = nxt_j\),即走到上图中黄边所指的位置,这样不断反复直到 \(s2_{j+1} = s1_{i+1}\)。
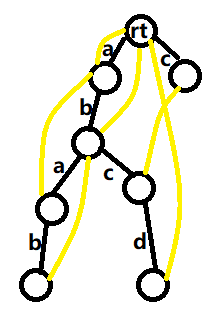
那么如果有多个模式串呢?我们总不能对所有模式串都做一遍这个转移图吧。我们可以建立一个 trie,然后对所有的点做一个这样的转移,这个就是 AC 自动机。炒个例子,对于 abca 与 abab,c,它们的自动机看上去是这样的:
(其中黑边是两个字符串所构造的 trie 上的边,黄边是转移边,显而易见黄边是有向的,从深度更深的节点向上连边)
注意这些边可能会从一个模式串连到另一个模式串上去,其条件是满足一个模式串的后缀与另一个模式串的前缀相同,比如 abcd 其中 abc 的后缀 c 与 c 的前缀 c 相同,所以连了一条边。额看懂图就基本上明白了吧 QWQ
我们令 \(fail_u\) 为 trie 中节点 \(u\) 所指向的节点编号(就是上面黄线的边)。有了 \(fail\) 我们就可以像 kmp 一样做匹配了,那么问题来了 \(fail\) 怎么求?
我们回忆一下,对于一个模式串,我们怎么求 \(nxt\) 的,其实就是和自己匹配,不断让模式串的指针往后走,走不了就往回按照 \(nxt\) 也就是失配边跳。
那么多个模式串呢?其实也差不多。假设我们在一个模式串中 \(x\) 位置,它的前驱位置 \(w\) 的 \(fail_{w}\) 已知。如果 \(w\) 到 \(x\) 的字符是 \(c\),即 \(trie_{w, c} = x\),那么 \(x\) 就可以沿着 \(fail_{w}\) 一直跳,如果 \(trie_{fail_{w}, c}\) 存在,那么 \(fail_x = trie_{fail_w, c}\)。相当于在 \(fail_w\) 与 \(w\) 后面都多了一个点。这么说可能不太清晰,比如说上面图里面最左边的叶子节点,它的父亲 \(fail_w\) 指向第一层的 a,它自己是被父亲的 b 二次,很巧 \(trie_{fail_w, c}\) 即第一层的 a 存在一个儿子 b,也就是说可以把这个 a 后面接一个 b,即 \(fail_x = trie_{fail_w, c}\)。
如果 \(trie_{fail_{w}, c}\) 不存在,那么使 \(w = fail_{w}\),然后继续看 \(trie_{fail_w, c}\) 存不存在。这个其实很像 kmp 对吧。
由于推的过程都是从层次较浅的节点开始推,所以我们采用 bfs 来遍历整颗 trie,对于每个节点就按照上面的方法找 \(fail\)。
其实还有一个小操作,当 \(x = 0\) 时,那么让 \(trie_{w, c} = trie_{fail_w, c}\)。这其实就是前面把 \(w = fail_w\) 然后一直跳的操作,只不过是重新连了一条边,代码看上去更简洁罢了。
怎么匹配呢?其实和 kmp 差不多,就是先看看存不存在点,不存在就跳 \(fail\),直到跳出来。如果是一个字符串的结尾那么就说明匹配成功了。
那么问题来了,这会匹配所有的吗?答案是肯定的。因为匹配到一个模式串的结尾,这个结尾又有 \(fail\) 去跳到另一个结尾继续找。大家可以拿 ababcd 手玩一下上面的图。
简单板子代码
//SIXIANG
#include <cstdio>
#include <iostream>
#include <queue>
#include <cstring>
#define MAXN 1000000
#define QWQ cout << "QWQ" << endl;
using namespace std;
char str[MAXN + 10], txt[MAXN + 10];
int tot = 0, trie[MAXN + 10][30], fail[MAXN + 10], cnt[MAXN + 10], ind[MAXN + 10];
void Insert(char *str, int id) {
int now = 0, len = strlen(str);
for(int p = 0; p < len; p++) {
int c = str[p] - 'a' + 1;
if(!trie[now][c]) trie[now][c] = ++tot;
now = trie[now][c];
}
cnt[now]++;
ind[now] = id;
}
void Build() {
queue <int> que;
for(int p = 1; p <= 26; p++)
if(trie[0][p]) que.push(trie[0][p]);
while(!que.empty()) {
int w = que.front(); que.pop();
for(int c = 1; c <= 26; c++) {
int x = trie[w][c];
if(!x) {
trie[w][c] = trie[fail[w]][c];
continue;
}
fail[x] = trie[fail[w]][c];
que.push(x);
}
}
}
int Query(char *txt) {
int ans = 0, nn = 0, len = strlen(txt);
for(int p = 0; p < len; p++) {
int c = txt[p] - 'a' + 1; nn = trie[nn][c];
for(int now = nn; cnt[now] != -1 && now; now = fail[now]) {
ans += cnt[now];
cnt[now] = -1;
}
}
return ans;
}
int main() {
freopen("test.txt", "r", stdin);
int n; scanf("%d", &n);
for(int p = 1; p <= n; p++)
scanf("%s", str), Insert(str, p);
Build();
scanf("%s", txt);
printf("%d\n", Query(txt));
}