给你长为 \(n\) 的正整数数组 \(a_i\) ,让你从中找有多少对 \((i,j)\) 满足 \(a_i,a_j\) 互质
\(n \leq 10^6\)
不错的一道题
考虑枚举 \(j\) ,看前面有哪些数和他互质。这时候问题看起来很像一个非常经典的问题:问前 \(x\) 个数中有多少数是 \(2\) 的倍数或 \(3\) 的倍数。
一眼容斥,因此考虑我们用一个桶 \(num_i\) 表示当前考虑的这些数中是 \(i\) 的倍数的数的个数。这时候发现答案就是 \(\sum\limits_{i=1}^{n} \sum\limits_{d|a_i} \mu(d) num_d\) ,朴素计算复杂度 \(O(nd(n))\)
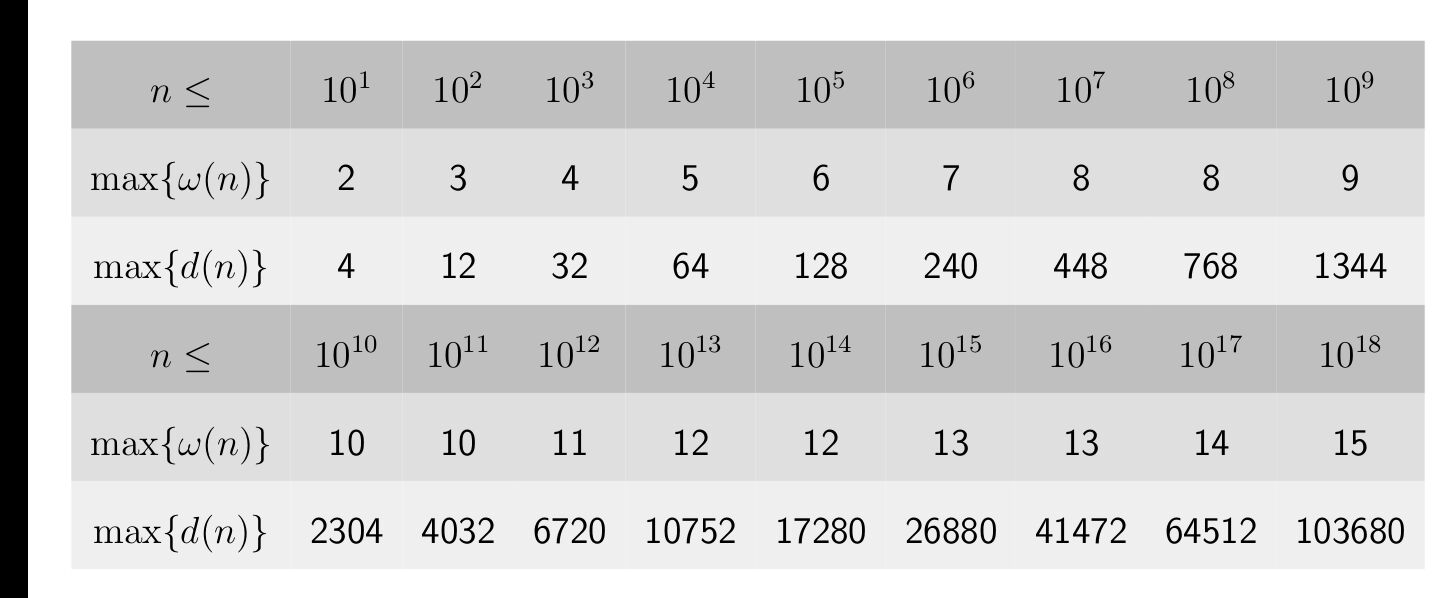
发现根据 \(\mu(i)\) 的定义,我们不如手动把那些含有平方因子的数剔除掉。具体的,我们对于一个数 \(O(\log A)\) 的分解质因数,然后对他的每个质因子枚举选不选即可。
复杂度 \(O(A + n\log A + n 2^{\omega(A)})\) ,这个复杂度是很难跑满的,足够通过
标签:log,复杂度,9F,mu,num,倍数,互质,模拟 From: https://www.cnblogs.com/fox-konata/p/17744740.html