正文

这是样例 1 第 1 组数据的图。

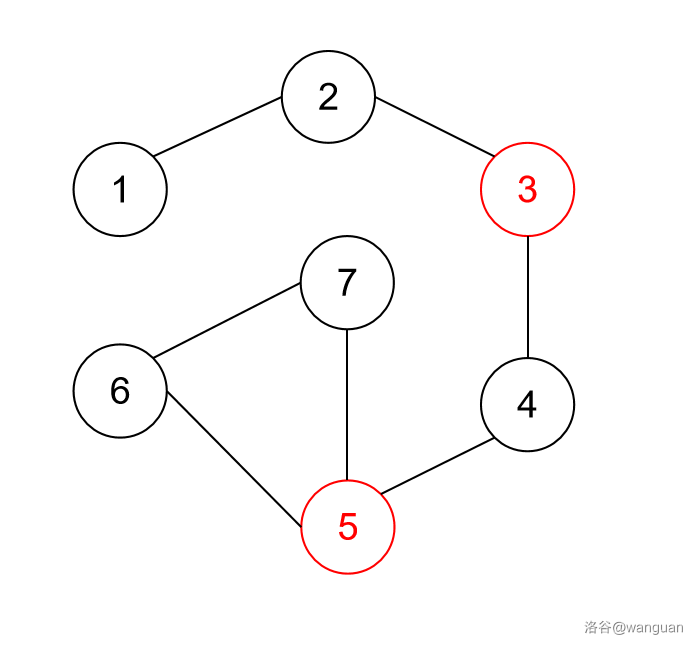
让我们观察一下，路径 1->6、1->7、2->6、2->7 是可行的，所以答案为 4。

上述路径中好像点 4 没有贡献？

再看看样例 1 第 2 组数据的图。

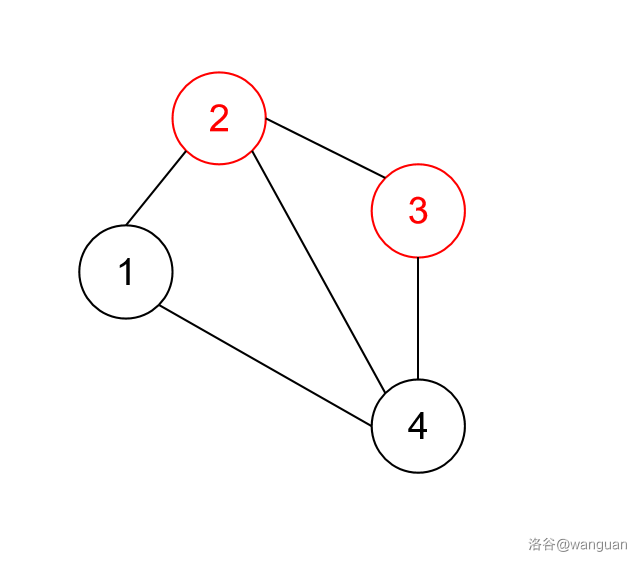
发现点 1 和点 4 相互之间存在其他路径，无需经过点 \(a\) 和点 \(b\)。

综上，我们可以知道：在 \(a\) 和 \(b\) 之间的任意路径上的点是不作贡献的。

可以看作 \(a\) 和 \(b\) 之间的路径是一个桥梁，桥梁的两边的点才是做出贡献的，我们将第 1 组数据的图改变一下，可以很清楚地理解。

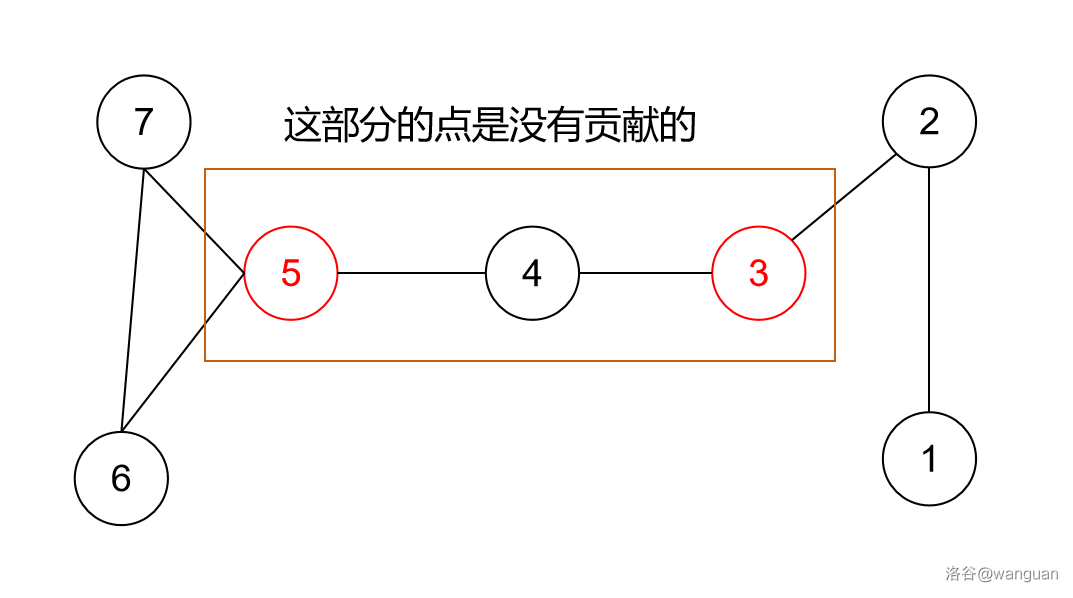
因此，我们只要找 \(a\)、\(b\) 隔开的点的数量，再将两边数量相乘（乘法原理）即可。

接下来，只要找隔开的点的数量就可以。

考虑 DFS，对 \(a\) 和 \(b\) 分别 DFS。假设从 \(a\) 开始搜，若有一分支搜到 \(b\)，则将该分支贡献清零，因为该分支上的点在 \(a\)、\(b\) 之间，没有贡献（既与 \(a\) 相连，也与 \(b\) 相连）。\(b\) 点同理。

那就可以写代码力。

#define by_wanguan
#include<iostream>
#include<vector>
#include<cstring>
#define int long long
const int N=2e5+7;
using namespace std;
int T,n,m,a,b;
vector<int> g[N];
bool vis[N],vis_[N];
inline int dfsb(int x){
  vis[x]=1;
  int ret=1;
  if(x==a) {vis[x]=0; return 0;}
  for(int &i: g[x]){
    if(vis[i]) continue;
    int s=dfsb(i);
    if(s==0&&x!=b) {vis[x]=0; return 0;}
    ret+=s;
  }
  return ret;
}
inline int dfsa(int x){
  vis_[x]=1;
  int ret=1;
  if(x==b) {vis_[x]=0; return 0;}
  for(int &i: g[x]){
    if(vis_[i]) continue;
    int s=dfsa(i);
    if(s==0&&x!=a) {vis_[x]=0; return 0;}
    ret+=s;
  }
  return ret;
}
signed main(){
  ios::sync_with_stdio(false),cin.tie(0);
  cin>>T;
  while(T--){
    cin>>n>>m>>a>>b;
    memset(vis,0,sizeof vis);
    memset(vis_,0,sizeof vis_);
    for(int i=1;i<=n;i++) g[i].clear();
    for(int i=1,a,b;i<=m;i++)
      cin>>a>>b,
      g[a].emplace_back(b),
      g[b].emplace_back(a);
    int aa=dfsa(a)-1,bb=dfsb(b)-1;
    cout<<aa*bb<<'\n';
  }
}

提交记录。