PBN三板斧之飞越转弯TF/CF航段

数据库编码在航电系统中的作用是毋庸置疑的，对于编码的理解往往需要结合应用场景来进行分析，必要的时候还需要放到模拟机中进行验证，才能够真正找出飞行程序设计与机载系统的最终解释之间的差别。

今天要聊的飞越转弯衔接TF/CF航段的话题,是在今年一次研讨会议中，让我觉得眼界打开，对个人的程序设计理念都产生了很大触动的一个问题。

TF与CF航迹编码从字面意思来看只有一字之差，TF（Track to a Fix）沿航迹至定位点，CF（Course to a fix）沿航径至定位点。

首先它们的应用场景是不同的，TF编码作为最普遍使用的编码方式，简单来说是用在点到点的航段连接中。

CF编码过去常用在最后进近，但目前最后进近主用TF编码。CF编码目前更多的是用在复飞及离场的初始转弯段，用来连接CA或FA航段。

如果CF的航径恰好通过前一航段的结束点（比如复飞点）,这种情况下，CF与TF的用法及保护区是没有差别的，就像下面这张图例所表达的意思。

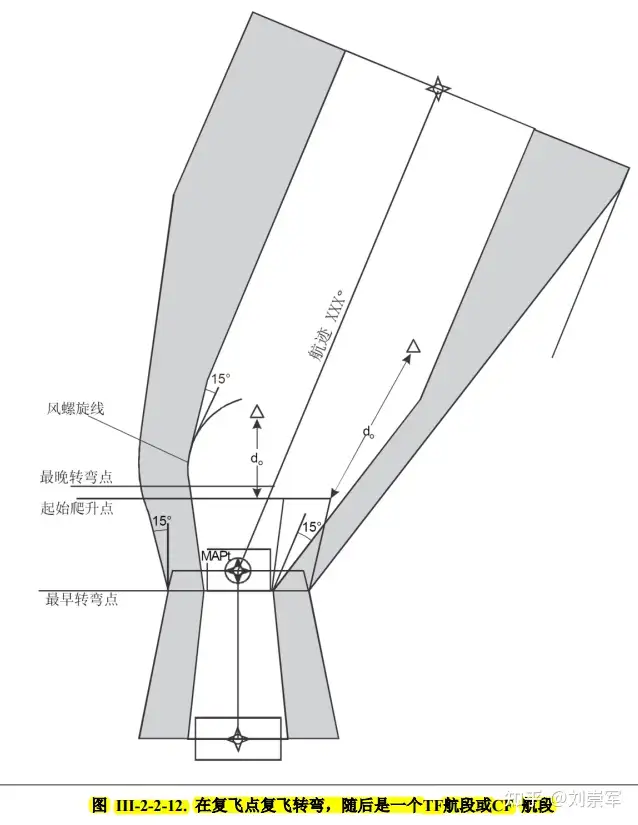
上图中，TF/CF航迹是通过复飞点直连下一点来定义的，这个航段无论是采用TF或CF编码，并没有差别。其它情况下，它们还是存在一些差别的。

飞越点衔接TF航段的图例在8168中给的相对比较充分，计算飞越点稳定距离的图例中，实际上就是一个衔接TF航段的用法。

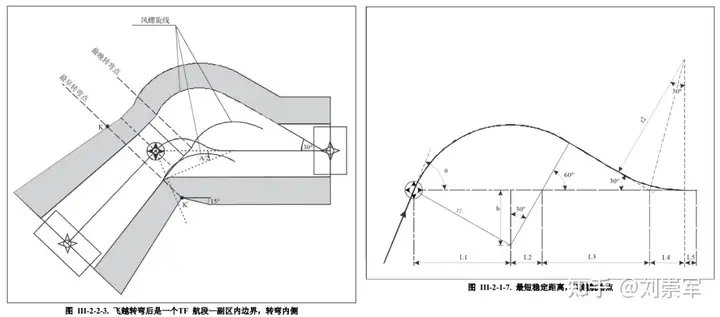
单独看飞越转弯衔接TF航段保护区，它的转弯外边界部分更像是将DF航段保护区与旁切转弯保护区拼接在一起的结果。按照前文的命名习惯，可以称为“移花接木”。

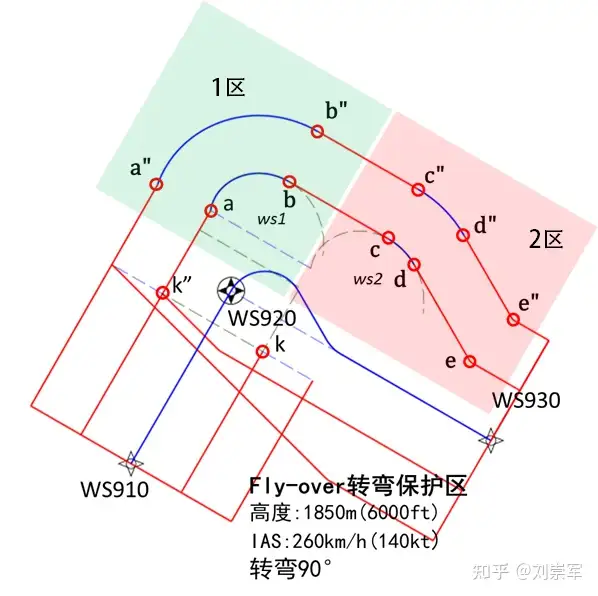
上图中的1区是直接使用的风螺旋，FlyOver-DF以及定高转弯保护区中都可以看到类似的画法。2区采用了30°内收的计算方法，这与旁切转弯的收缩方式是一致的。

这两种计算方法之前都有提到，用角度来表示，就是下图中的内容。

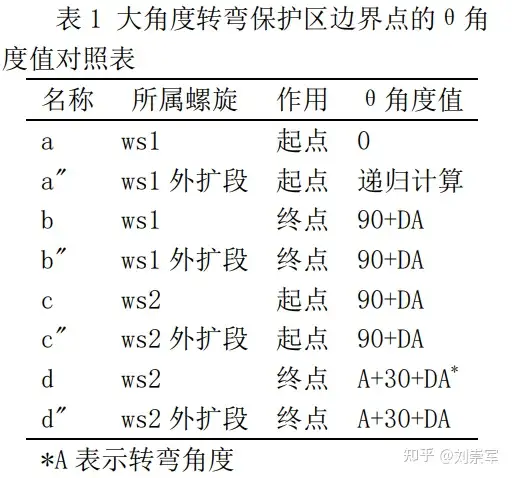
需要注意的是，当转弯角度不同时，出航航段的保护区可能出现30°内收线，也可能直接与风螺旋相交（不出现e点），也可以是直接与风螺旋的公切线相交。以下分别是转弯角度为90°、60°、50°情况下的保护区样例。

离场定高转弯CF航段的转弯外边界与前面讨论的FlyOver-TF方式是一致的，但转弯内边界存在较大差异。

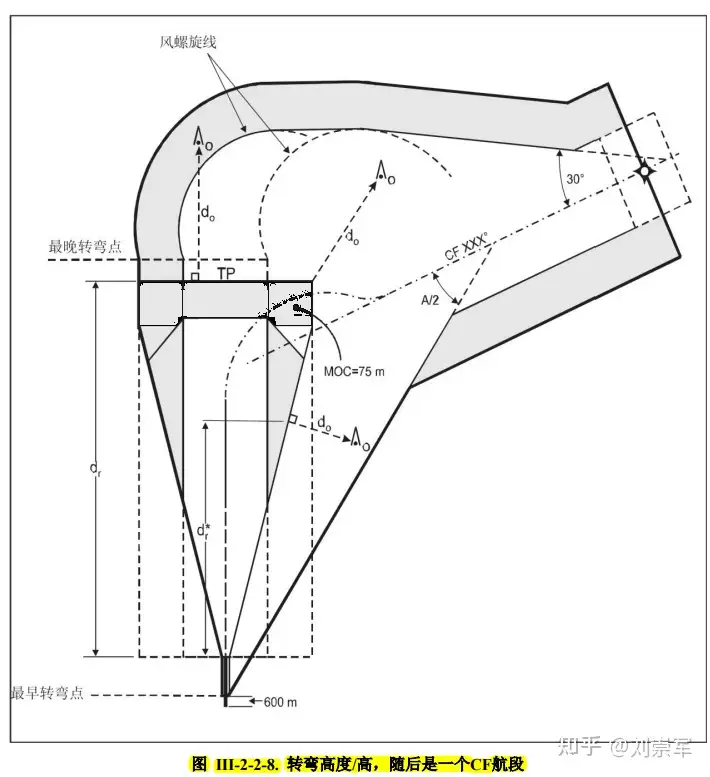
如上图所示，定高转弯CF航段，转弯内边界是以转弯角度的一半（A/2）来连接到下一航段，连接区内按照全主区的超障余度来计算。

对于转弯角度较小的情况，可以参考上面的图例来进行绘制，但对于转弯角度较大的情况，比如通过CF航段直接引导航空器飞至三边方向的情况下，CF航段的实际轨迹和保护区的画法就成了玄学，没有统一的标准。

某机场存在一个CA 450英尺转弯，之后CF 313°磁航迹飞向下个航路点的离场程序。

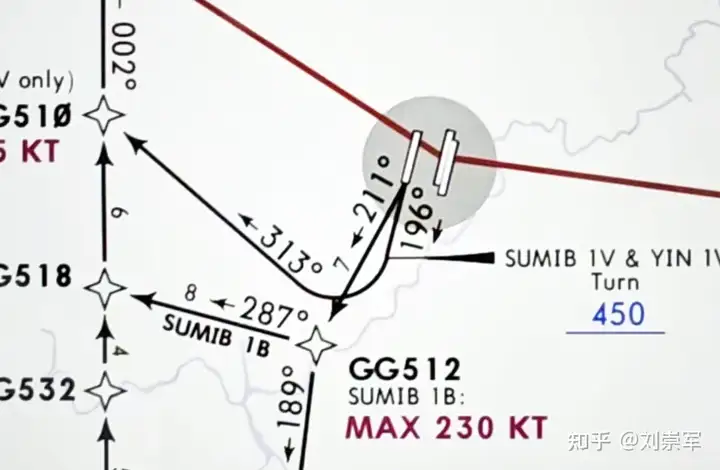
航图中转弯段通过一段圆弧来表示，机载数据库显示该段程序的轨迹如下图所示：

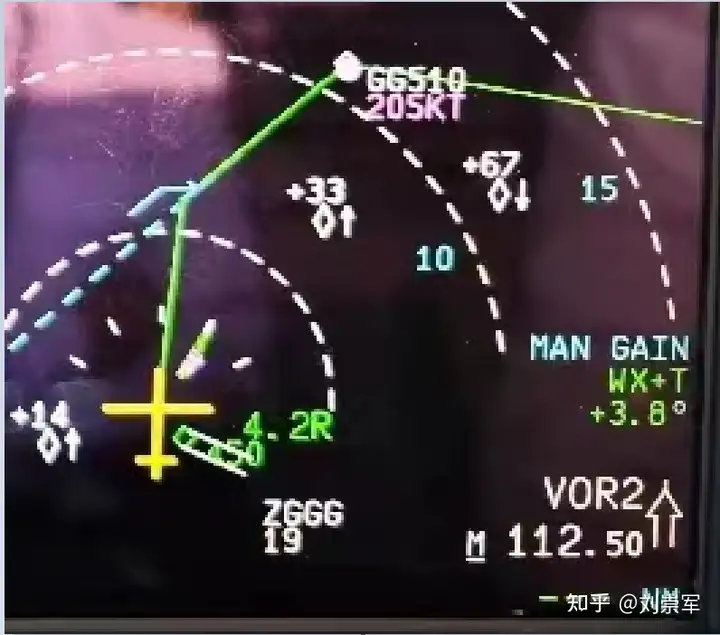
上图中的轨迹显示，航空器以大约45°的夹角切入到313°磁航迹，基本上算是符合程序设计的意图。

对于另外一些机型（主要为波音系列机型），机载数据库显示的轨迹差异会更大一些。

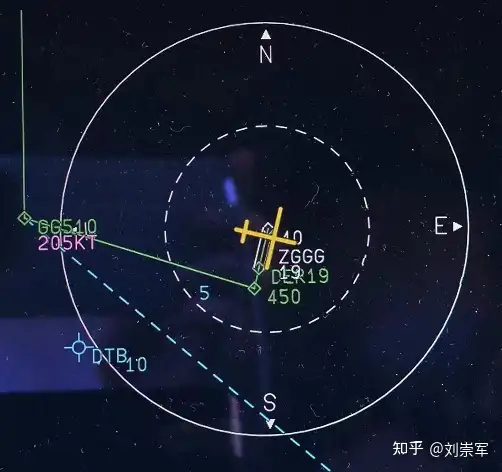
对于上图所示的这种机型，CF航段中指定的磁航迹将被忽略，实际轨迹更接近DF的飞行方式。

为了对以上的结论进行验证，我们在模拟软件中对空客、波音系列的主流机型逐个进行了对比。结果发现，空客系列机型对于CF编码的支持程度远好于波音系列机型，波音机型中多数都会将CF编码解释为DF的飞行方式，即使是最新的机型这一问题也没有明显的改变。因此，波音机型与空客机型对数据库的解析存在差异，这是影响飞行程序可用性的一个关键因素。

对于飞行程序设计人员来说，符合规范是最基础的要求，在此之上，应该重点关注程序编码在数据库中的表现。目前来看，TF编码对各类机型来说解析的较为一致，CF编码存在差异，需重点关注。

从CF编码的细节来看，航迹改变的角度越大，不同机型对路径解析的差异就越大。因此在使用CF编码时，航迹改变的角度应尽量减小，建议按照旁切转弯的标准，控制在120°以内。

对于使用CF编码直接引导航空器从一边转弯加入三边的程序，考虑到波音机型有可能是以DF方式在执行该段轨迹，建议设计人员按照DF转弯内边界的评估方法，从转弯最早点向航段终点进行补充评估（下图中红线包含的区域），确保在DF方式下，最早航迹满足安全要求。

三板斧系列文章的第三篇内容就是这些了，通过运用风螺旋的计算方法，主要解决了飞越点接TF/CF转弯航段外边界的保护区精确计算问题，对于CF转弯内边界的轨迹差异给出案例并提供了建议。

PBN飞行程序转弯保护区中大部分内容都与旁切或飞越有关，希望我们这入门级的三板斧能够帮助大家更好的理解PBN转弯保护区的绘制方法。

数据库编码以及模拟机验证很可能是将来“卷”完程序设计自动化之后，下一个必“卷”的内容，希望大家的注意力能向这个方向多投入一些，本公众号后续也会增加这个方向的话题，欢迎关注，感谢支持。