题目大意
有 \(n\) 个杯子,第 \(i\) 个杯子里装有 \(W_i\) 升水,且有 \(n\) 对正整数 \(l_i,r_i\)。Yuri 和 Muri 两人在玩一个游戏:两人轮流进行操作,最先不能进行操作者输。
一次操作定义为:操作者选择一个杯子 \(i\),从中喝掉 \(x_i\) 升水。对于两个人,都要满足 \(x_i\in[l_i,\min(r_i,W_i)]\),且对于 Yuri 要满足 \(x_i\) 是有理数、对于 Muri 要满足 \(x_i\) 是无理数。
现在,Muri 可以选择先后手,若两人以最优策略行动,问谁会获胜。
思路
我们发现,在一定的精度内,相距很近的有理数与无理数之间对胜负性的影响并不大,胜负状态间的转折点只是一些整数点,于是可以把 Yuri 和 Muri 的取数值域分别看做是 \([l_i,r_i]\) 和 \((l_i,r_i)\)。如下图(表示进行一次操作之后能得到的 \(W^\prime_i\)。上面为 Yuri 的,下面为 Muri 的,下同):

接下来我们尝试打表这个博弈的 SG 函数。
以 Yuri 为例。我们发现,当 \(r_i\) 足够大时,前一部分的 SG 具有一定的规律性:
- 若 \(W_i\in [0,l_i)\),此时无法进行操作,SG 为 \(0\);
- 若 \(W_i\in [l_i,2l_i)\),此时可以转移到 SG 为 \(0\) 的部分,故 SG 为 \(1\);
- 若 \(W_i\in [2l_i,3l_i)\),此时可以转移到 SG 为 \(0\) 和 \(1\) 的部分,故 SG 为 \(2\);
- ……
所以,在 \(W_i\) 较小的时候,SG 呈现这样一个“阶梯”形。等到遇到了 \(r_i\),SG 又会有相应的改变。取整数 \(t\),满足 \(tl_i < l_i+r_i\le (t+1)l_i\),那么,继续分类讨论:
- 若 \(W_i\in[tl_i,l_i+r_i)\),根据上面,SG 为 \(t\);
- 若 \(W_i\in[l_i+r_i,2l_i,r_i)\),此时,如下图,无法转移到 SG 为 \(0\) 的部分,故 SG 为 \(0\);
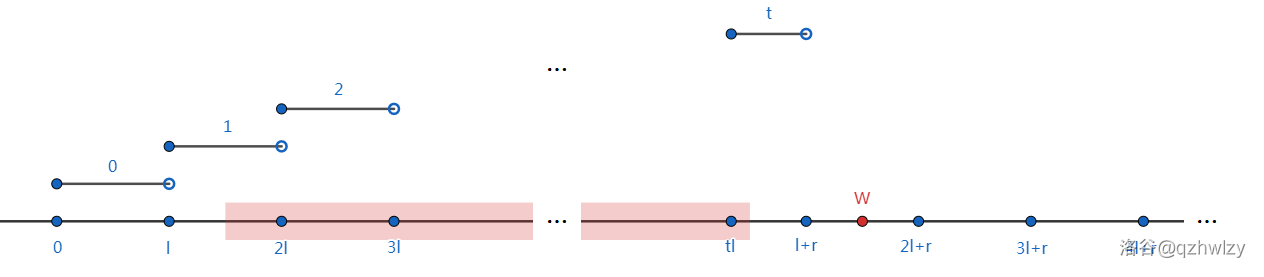
- 若 \(W_i\in[2l_i+r_i,3l_i,r_i)\),此时无法转移到 SG 为 \(1\) 的部分,故 SG 为 \(1\);
- ……
如此下去,得到 Yuri 的最终的 SG 如下图:
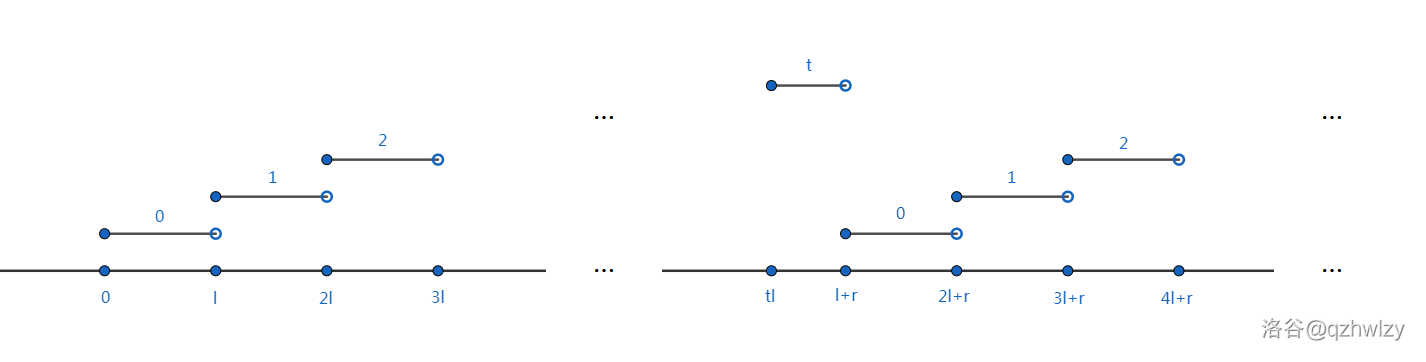
同理,我们可以得到 Muri 的 SG,总体如下图所示,它与 Yuri 的只在某些整点处的取值略有不同,大体上是一样的,这也是为什么我们可以把取数值域进行近似的原因。
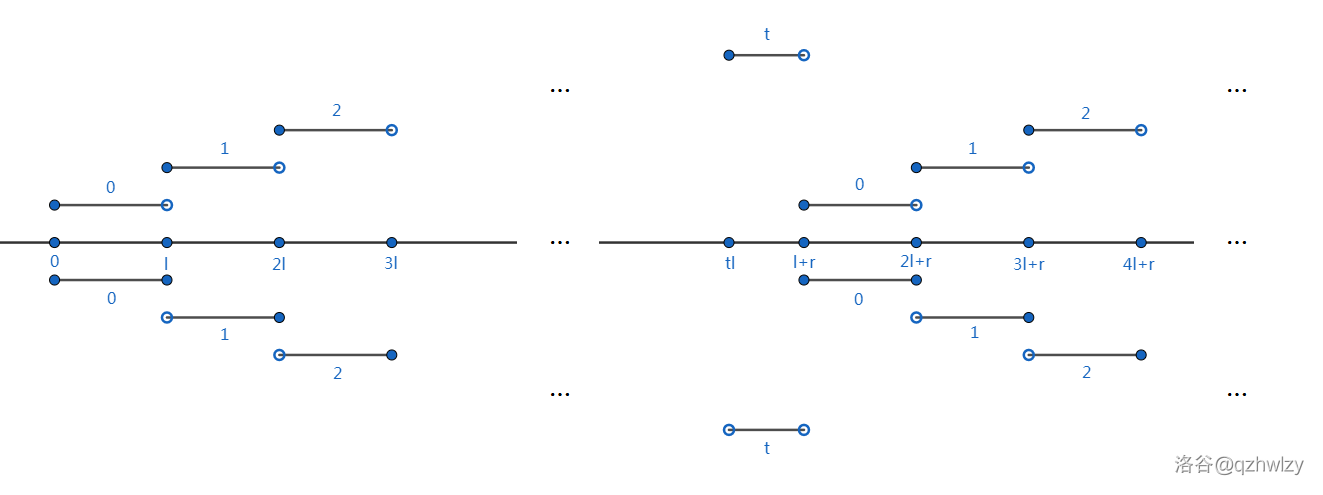
下称 SG 突变的点为转折点,即满足 \(l_i\ |\ W_i\bmod(l_i+r_i)\) 的点。
那么,对于这个非公平的博弈,SG 是否仍然有用呢?显然是有的。在非转折点上,SG 仍然可以判断胜负性,若 SG 为 \(0\) 则先手必败,否则先手必胜。在转折点上的情况下面会讲。
注意到在本题中,Muri 取数值域为 Yuri 取数值域的真子集,所以若在 Muri 的视角下其是必败的(故下面两种情况下的“SG”指的是 Muri 的),Yuri 可以只用 Muri 的取数值域让其必败。故,在「SG 为 \(0\) 且 Muri 先手」或「SG 不为 \(0\) 且 Yuri 先手」时 Yuri 必胜。
上面提到在转折点上,SG 可能不奏效。在官方题解中,定义了包括这些转折点在内的一类点,称为“「不正」点”,根据 std,本文中将其翻译为“作弊点”。若此时水量在作弊点,那么 Yuri 可以通过操作改变 SG 对自己的不利。作弊点有以下两类:
-
所有转折点,即满足 \(l_i\ |\ W_i\bmod(l_i+r_i)\) 的点。
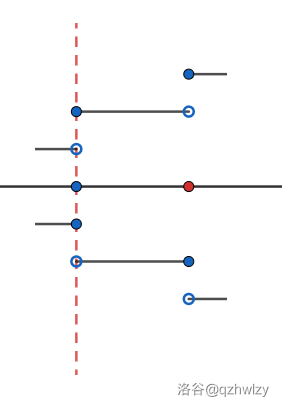
此时若 Yuri 先手,假设此时有 \(p(l_i+r_i)+ql_i\) 的水,SG 为 \(q\),其可以选择喝 \(l_i\) 的水,此时水量 \(W=p(l_i+r_i)+(q-1)l_i\),SG 为 \(q-1\),但是,此时 Muri 操作后能够到达的 \(W\in((p-1)(l_i+r_i)+ql_i,p(l_i+r_i)+(q-2)l_i)\),没有 SG 为 \(q\) 的点,所以就无法保证必胜。 -
\(W\in[2l_i,l_i+r_i]\cap\mathbb{Q}\) 中的点。
此时 Yuri 可以把水量转移到 \(l_i\) 从而保证必胜,因为此时只有其可以操作这杯水。注意一定得是有理的,有人忘了这个前提以为自己 hack 了 std。
于是,我们可以判断,若为「SG 为 \(0\) 且 Yuri 先手」的情况,若其中有作弊点,则 Yuri 必胜,否则 Muri 必胜。若为 「SG 不为 \(0\) 且 Muri 先手」的情况,则若 Muri 第一步能保证去除所有作弊点,则 Muri 必胜,否则 Yuri 必胜。注意这里的 SG 也应该在 Muri 的视角下,因为作弊点是对于 Yuri 而言的。
所以,整个过程我们只需要统计初始 Muri 视角下的 SG 和,然后判断是否有 Muri 必胜的情况,若有则 Muri 必胜,否则 Yuri 必胜。
#include<iostream>
#include<cstdio>
#define maxn 200005
using namespace std;
int n,w[maxn],l[maxn],r[maxn],sg[maxn],sgsum=0;
int main(){
scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d%d%d",&w[i],&l[i],&r[i]);
for(int i=1;i<=n;i++){int res=w[i]%(l[i]+r[i]); sgsum^=(sg[i]=max(0,((res-1)/l[i])));} // calculate sgsum
if(sgsum==0){ // Muri can win if and only if there's no "cheating point"
bool flag=0; for(int i=1;i<=n&&!flag;i++){
int res=w[i]%(l[i]+r[i]);
flag|=((res%l[i]==0)||(w[i]<l[i]+r[i]&&w[i]>=2*l[i])); // determine if there's "cheating point"
} if(flag) printf("Yuri"); else printf("Muri");
}else{ // Muri can win if and only if there's one way to make sgsum==0 and there's no "cheating point"
int num=0,pos=0; for(int i=1;i<=n;i++)
{int res=w[i]%(l[i]+r[i]); if((res%l[i]==0)||(w[i]<l[i]+r[i]&&w[i]>=2*l[i])){num++; pos=i;}}
if(num>1){printf("Yuri"); return 0;} // Muri will never win since the number of "cheating point" > 1
if(num==0){printf("Muri"); return 0;}// if there's no "cheating point", Muri can always win
// otherwise, if there's exactly one "cheating point"
int res=sgsum^sg[pos],mmax=(l[pos]+r[pos]-1)/l[pos]; // new grundy number and maximum grundy number
if(res>mmax){printf("Yuri"); return 0;} // new grundy number won't exist
int left=res*l[pos],right=min(res*l[pos]+l[pos],l[pos]+r[pos]);
int T=max(0,w[pos]/(l[pos]+r[pos])-(sg[pos]<res));
if(w[pos]<=l[pos]+r[pos]){if((res==0||res==1)&&res<sg[pos]) printf("Muri"); else printf("Yuri"); return 0;}
// determine if (left+T*(l+r) , right+T*(l+r)) ∩ (w-r , w-l)
if(!(right+T*(l[pos]+r[pos])<=w[pos]-r[pos]||left+T*(l[pos]+r[pos])>=w[pos]-l[pos]))
printf("Muri"); else printf("Yuri");
}
return 0;
}
/*
2
16 3 5
7 5 6
2
17 3 7
10 3 7
*/