酒店之王
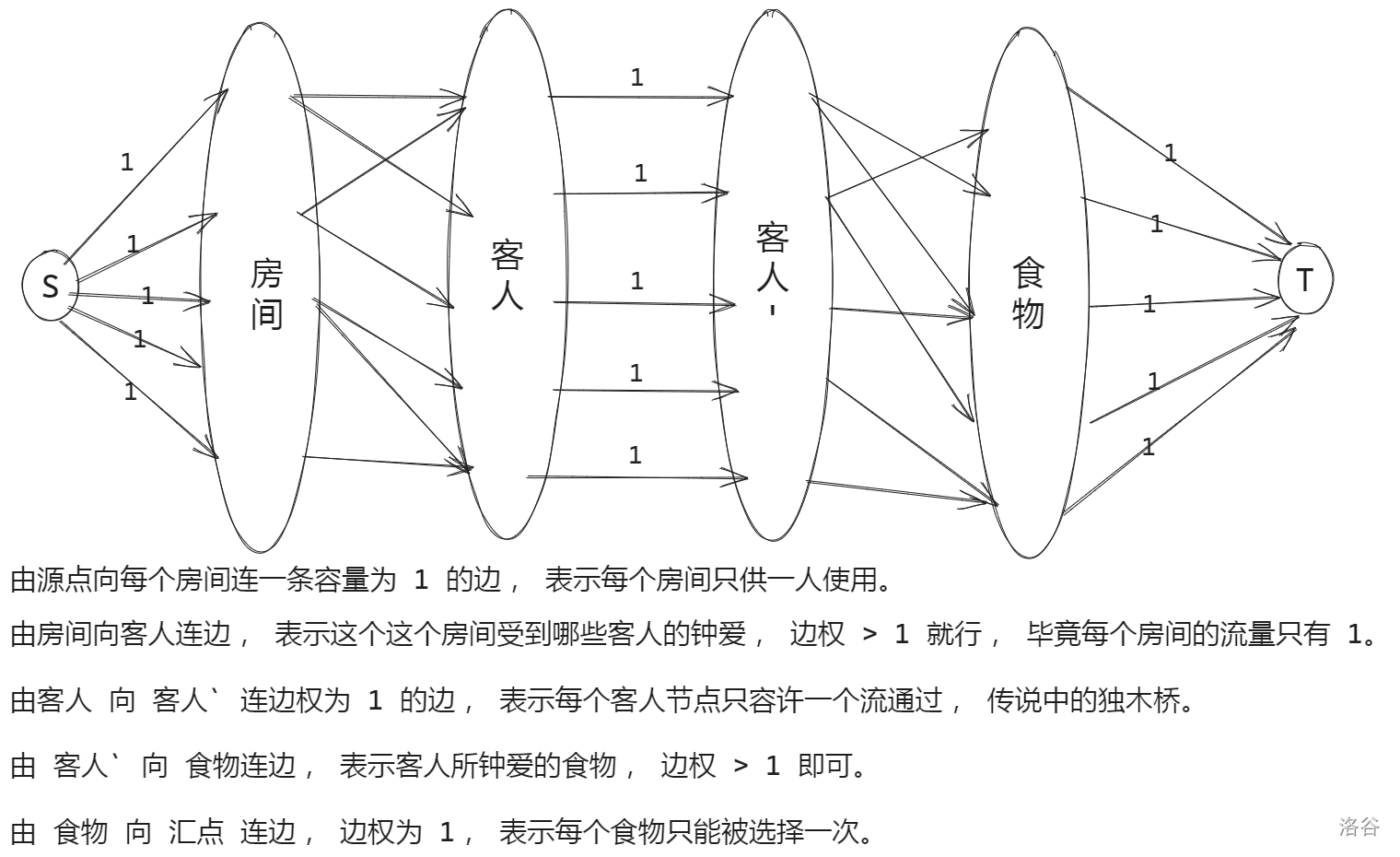
考虑到 房间 和 食物都和客人有关, 而 房间 和 食物间没有明显关系, 我们考虑将 客人放在所建图的中间, 以此来联系。 而这时一个从源点出发到达汇点的流即表示既选择了想要的房间, 又选择了想要的食物。
但我们考虑一个问题, 由于每个人想要的房间可能不止一个, 那么由房间转移到一个客人再转移到食物的流可能不止一个, 即造成每个人可能选择了两份不同的他喜爱的房间和食物, 这个人的答案统计了两遍。
为了解决这个问题, 我们要设法强迫每个人只能选择一个房间, 即只有一个流可以通过一个客人节点转移到食物上。 因此, 我们有以下建图的方法 :
最小路径覆盖问题
小M的作物
首先, 像这种二选一的问题, 我们一般联想到最小割。
从模型的角度考虑, 最小割实际上是将一个图分割成两个不相连的部分所需的最小代价。 对应到这个题上来讲, 我们的最小代价实际上就是那些我们无法满足的条件的价值和。 将图划分成两个部分, 实际上对应每个节点选择在 A 处 还是 在 B 处。 至于那些留下来的, 指向源点 和 汇点的边, 即为两个部分分别产生的价值。
这样的话, 我们该如何建图?
对于单独的作物种植, 由于 A 和 B 间没有直接联系, 我们将作物放在中间, 源点 和 汇点分别在两边引出 A 和 B 的具体位置。 这样的话, 我们的 \(S - T\) 割就势必要将 \(A \rightarrow u\) 和 \(u \rightarrow B\) 这两条边之一切断, 来保证 \(S\) 和 \(T\) 的不连通性。
对于组合的作物来讲, 我们也考虑上述方式, 构造一种建边方式使得 我们要么计算 组合的价值, 要么放弃组合的价值。
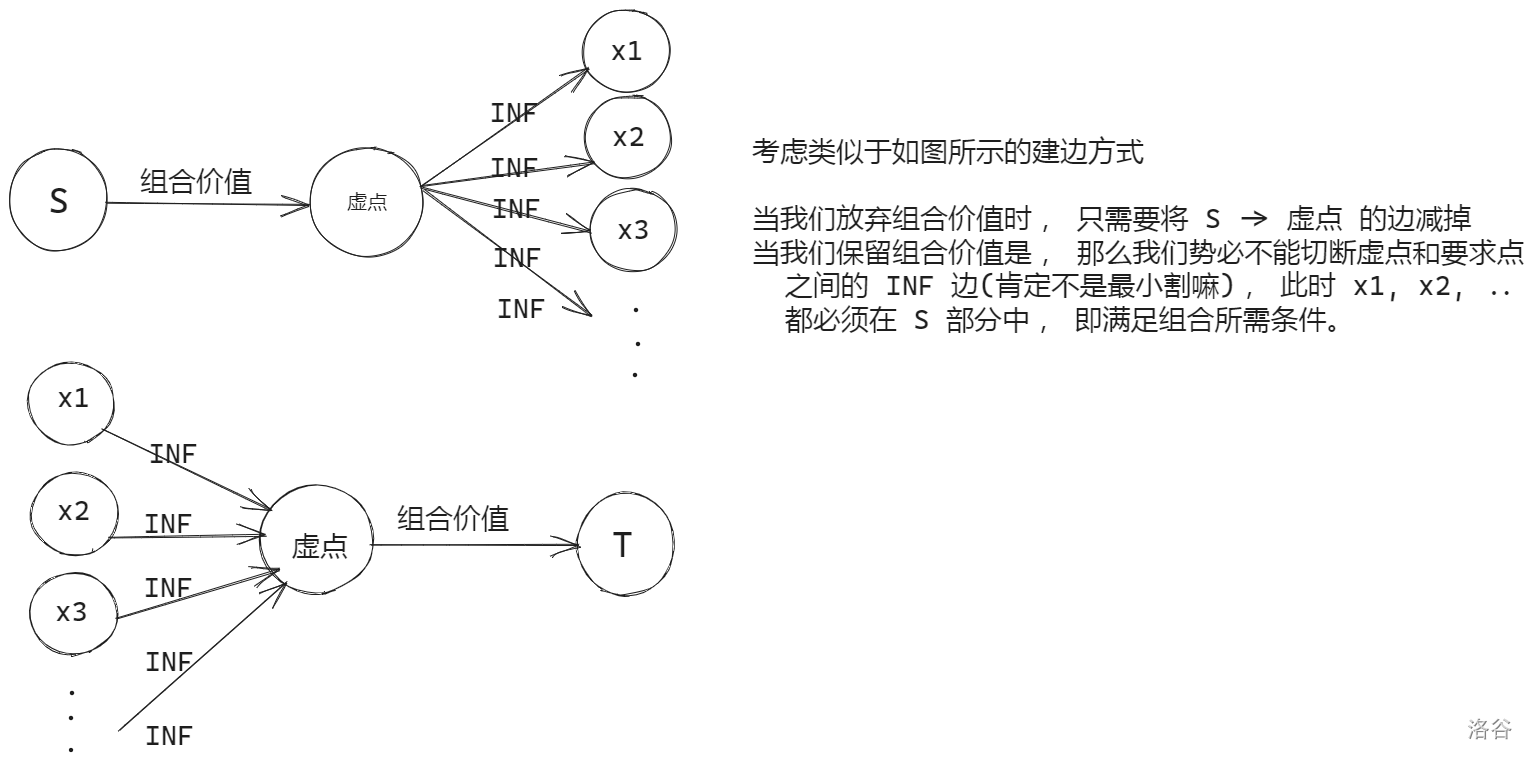
至此, 我们只需要求出最小割, 再用总价值减去它即可得到最终答案。
人员雇佣
相较于 小M的作物, 这道题提供了更一般的情况, 即使组合的一部分也会具有意义。
我们不可能对每两个经理建立一个组合, 这样会使点数达到 \(O(n ^ 2)\)。
考虑类似 小M的作物 的建图方式建议如下图所示 模型 :
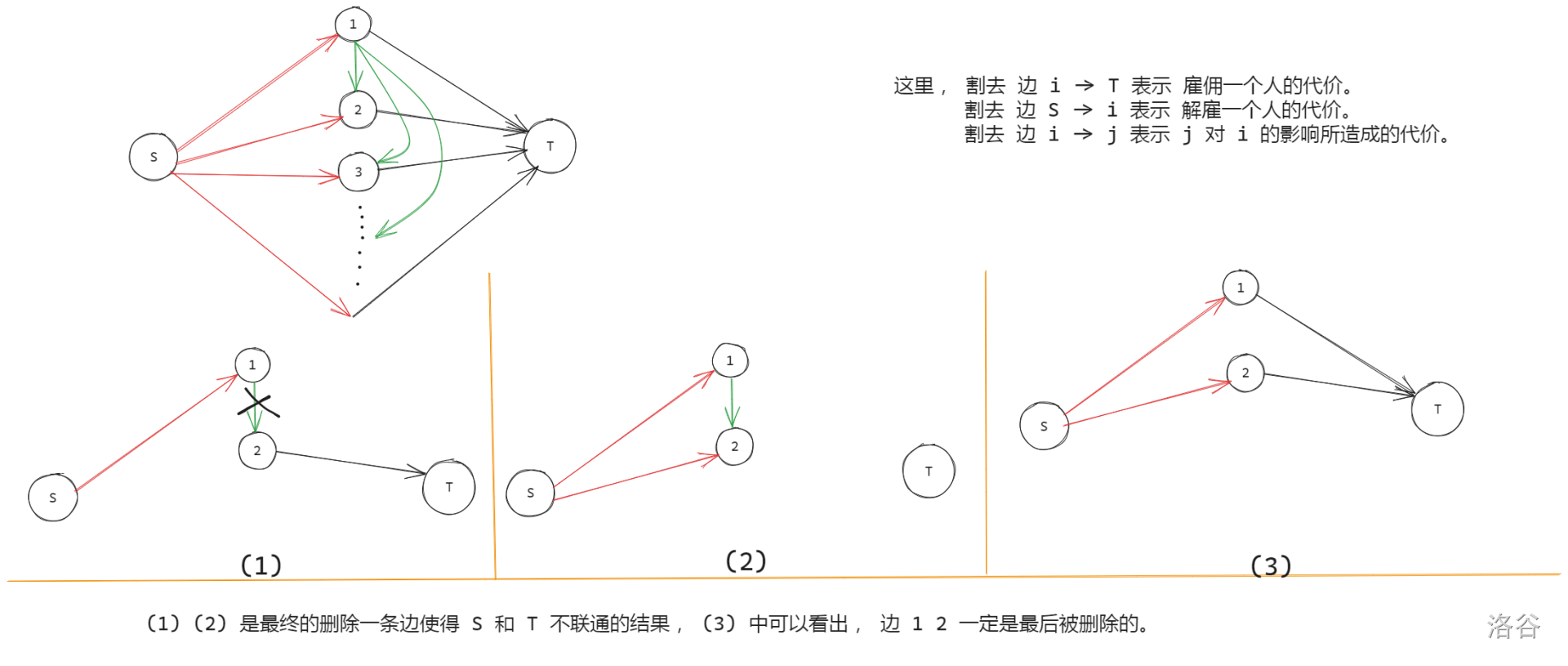
奶牛的电信
这个题很明显是求最小割的问题。 但不同点是, 这里割的是 点 而不是边。
直接建图跑最小割所得到的是最少需要中断几条通信线路。
既然我们不能拆边, 那么我们将原图中的边容量设为 INF; 既然我们可以以 \(1\) 的代价拆点, 那么我们将图中的点一分为二, 分别记录入边 和 出边, 对于 拆开的两个点, 我们用容量为 \(1\) 的边连接, 表示拆除它的代价。
圈地计划
我们考虑类似于 小M的作物 建图。
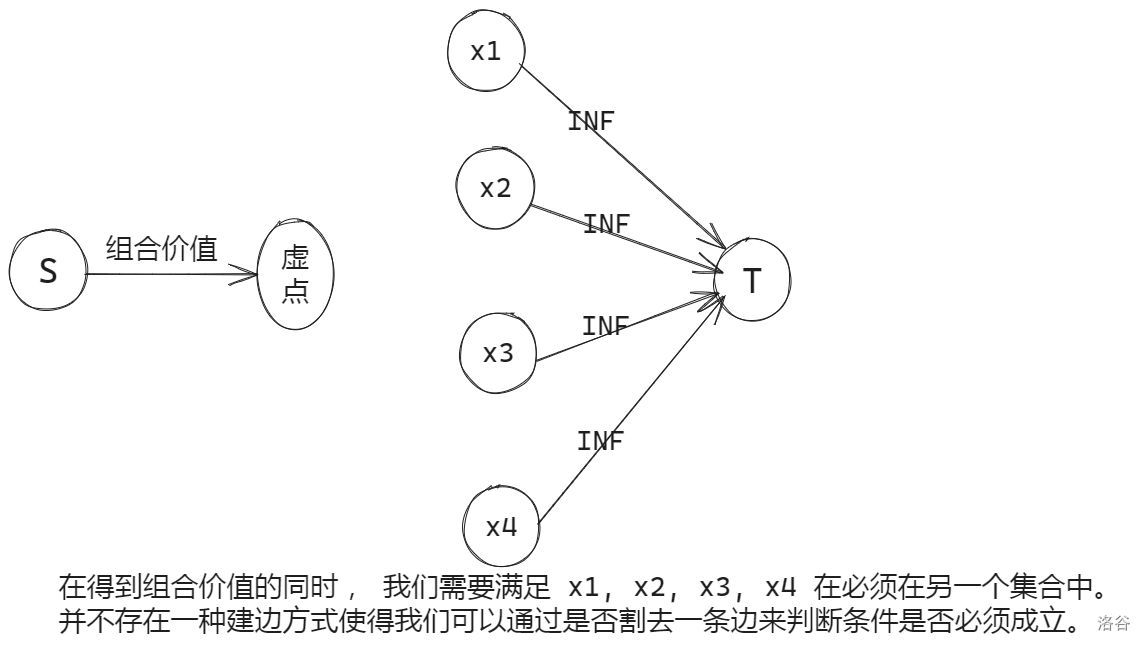
寻找这种组合的规律,我们发现:

我们考虑转化题意,将两个位置要选择不一样才会有附加权值 转变为
变成了两个位置集合相同才会有附加权值。

简单来讲,我们将哪些 原来是 \(S \rightarrow x\) 的边等价变换为 \(x \rightarrow T\),哪些 原来是 \(x \rightarrow T\) 的边等价变换为 \(S \rightarrow x\)。通过这种方式,我们使一个点 连线 集合 A 和 它周围的点 连线 集合 B 的边集中到一个集合中,以方便处理。
最后求一遍最小割即可。
餐巾计划问题
一般来讲, 如果一个事件 发生时是有阶段的, 我们可以考虑将该事件按照阶段划分拆成几个点, 分别维护该阶段发生的特殊条件。
对于本题来讲, 我们考虑如下的建图方式 :
-
从原点向每一天晚上连一条流量为当天所用餐巾 \(x\) ,费用为 \(0\) 的边, 表示每天晚上从起点获得 \(x\) 条脏餐巾。
-
从每一天早上向汇点连一条流量为当天所用餐巾 \(x\),费用为 \(0\) 的边,每天白天, 表示向汇点提供 \(x\) 条干净的餐巾, 流满时表示第 \(i\) 天的餐巾够用。
-
从每一天晚上向第二天晚上连一条流量为
INF,费用为 \(0\) 的边,表示每天晚上可以将脏餐巾留到第二天晚上(注意不是早上,因为脏餐巾在早上不可以使用。 -
从每一天晚上向这一天 + 快洗所用天数 \(t_1\) 的那一天早上连一条流量为
INF, 费用为快洗所用钱数的边,表示每天晚上可以送去快洗部,在地 \(i + t_1\) 天早上收到餐巾 。 -
同理, 从每一天晚上向这一天 + 慢洗所用天数 \(t_2\) 的那一天早上连一条流量为
INF,费用为慢洗所用钱数的边, 表示每天晚上可以送去慢洗部, 在地\(i + t_2\) 天早上收到餐巾 。 -
从起点向每一天早上连一条流量为
INF, 费用为购买餐巾所用钱数的边, 表示每天早上可以购买餐巾。 注意,以上 \(6\) 点需要建反向边! \(3 \sim 6\) 点需要做判断(即连向的边必须 \(\le n\))