首页 > 其他分享 >AtCoder Beginner Contest 318 ABCDE

AtCoder Beginner Contest 318 ABCDE

时间：2023-09-22 20:12:48浏览次数：43  
标签：AtCoder 318 const idx int ll ABCDE cin vx

AtCoder Beginner Contest 318

A - Full Moon

思路：等差数列求项数

// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;

int main()
{
    ios::sync_with_stdio(false);   cin.tie(nullptr), cout.tie(nullptr);
    int n,m,p;
    cin>>n>>m>>p;
    if(n<m)
    {
        cout<<0<<"\n";
        return 0;
    }
    //a1 = m,ak = a1+(k-1)*p;
    //m+(k-1)*p = n
    //(n-m)/p+1
    cout<<(n-m)/p+1<<"\n";
    return 0;
}

B - Overlapping sheets

思路：小规模直接模拟即可。(不会吧不会吧，不会真的有人写扫描线吧，好的是我TAT)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 201000;
vector<int>vx;
vector<array<int,4>>event;;
int n,q,m;

struct info
{
    int minv,mincnt;
};

info operator+(const info &l,const info &r)
{
    info a;
    a.minv = min(l.minv,r.minv);
    if(l.minv==r.minv)a.mincnt = l.mincnt + r.mincnt;
    else if(l.minv<r.minv)a.mincnt = l.mincnt;
    else a.mincnt = r.mincnt;
    return a;
}

struct node{
    int t;
    info val;
}seg[N*8];

void update(int id)
{
    seg[id].val = seg[id*2].val+seg[id*2+1].val;
}

void settag(int id,int t)
{
    seg[id].val.minv = seg[id].val.minv+t;
    seg[id].t = seg[id].t + t;
}

void pushdown(int id)
{
    if(seg[id].t!=0)
    {
        settag(id*2,seg[id].t);
        settag(id*2+1,seg[id].t);
        seg[id].t = 0;
    }
}

void build(int id,int l,int r)
{
    if(l==r)
        seg[id].val = {0,vx[r]-vx[r-1]};//mincnt就是区间长度，比如对于第一段就是第1个端点-第0个端点
    else 
    {
        int mid = (l+r)>>1;
        build(id*2,l,mid);
        build(id*2+1,mid+1,r);
        update(id);
    }
}


void modify(int id,int l,int r,int x,int y,ll t){
    if(l==x&&r==y)
    {
        settag(id,t);
        return;
    }
    int mid = (l+r)/2;
    pushdown(id);
    if(y<=mid) modify(id*2,l,mid,x,y,t);
    else if(x>mid) modify(id*2+1,mid+1,r,x,y,t);
    else{
        modify(id*2,l,mid,x,mid,t),modify(id*2+1,mid+1,r,mid+1,y,t);
    }
    update(id);
}


int main()
{
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    cin>>n;
    for(int i = 1;i<=n;i++)
    {
        int x1,x2,y1,y2;
        cin>>x1>>x2>>y1>>y2;
        vx.push_back(x1);
        vx.push_back(x2);
        //y坐标,类型0,x坐标
        event.push_back({y1,1,x1,x2});
        event.push_back({y2,-1,x1,x2});
    }
    sort(event.begin(), event.end());
    sort(vx.begin(), vx.end());
    //去重
    vx.erase(unique(vx.begin(), vx.end()),vx.end());
    m = vx.size()-1;//段数=点数-1
    build(1,1,m);
    int prey = 0;
    int totlen = seg[1].val.mincnt;
    ll ans = 0;
    for(auto evt:event)
    {
        int cov = totlen;
        if(seg[1].val.minv==0)
            cov = totlen - seg[1].val.mincnt;
        ans += (ll)(evt[0]-prey)*cov;
        prey = evt[0];
        //第0个端点到第1个端点实际上对应线段树里面是1,1
        //相当于每个节点记录的是(l+1,r)的信息
        int x1 = lower_bound(vx.begin(), vx.end(),evt[2])-vx.begin()+1;
        int x2 = lower_bound(vx.begin(), vx.end(),evt[3])-vx.begin();
        if(x1>x2)continue;
        modify(1,1,m,x1,x2,evt[1]);
    }
    cout<<ans<<endl;
    return 0;
}

附上正常版本

#include <bits/stdc++.h>
using namespace std;

int s[200][200];
int main() {
    int n;
    cin >> n;
    int a, b, c, d;
    for (int i = 1; i <= n; i++) {
        cin >> a >> b >> c >> d;
        for (int j = a; j < b; j++) {
            for (int k = c; k < d; k++) {
                s[j][k]++;
            }
        }
    }
    int ans = 0;
    for (int i = 0; i <= 100; i++) {
        for (int j = 0; j <= 100; j++) {
            if (s[i][j] > 0) ans++;
        }
    }
    cout << ans << endl;
    return 0;
}

C - Blue Spring

思路：排序+贪心。如果当前买通票比普通票便宜，那就一定买通票，否则普通票。

// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
ll f[N];
int main()
{
    ios::sync_with_stdio(false);   cin.tie(nullptr), cout.tie(nullptr);
    ll n,d,p;
    cin>>n>>d>>p;
    for(int i = 1;i <= n; i++)
        cin>>f[i];
    sort(f+1,f+1+n);
    ll ans = 0,cnt = 0,sum = 0;
    for(int i = n;i >= 1;i--)
    {
        cnt++,sum+=f[i];
        if(cnt==d)
        {
            if(sum>p)
                ans += p;
            else ans += sum;
            cnt = 0,sum = 0;
        }
    }
    if(sum>p)
        ans += p;
    else ans += sum;
    cout<<ans<<"\n";
    return 0;
}

D - General Weighted Max Matching

思路：看到\(N\)只有\(16\)，一眼状压。枚举当前状态，\(1\)表示选了，\(0\)表示还没选，然后开始\(dp\).

考虑如何转移，在现在的状态下，要再选两个之前没选过的点且这两个点不能一样那就可以选。

// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
ll f[20][20];

int main()
{
    ios::sync_with_stdio(false);   cin.tie(nullptr), cout.tie(nullptr);
    int n;
    cin>>n;
    for(int i = 0;i < n; i++)
        for(int j = i+1;j < n; j++)
            cin>>f[i][j],f[j][i] = f[i][j];
    vector<ll>dp(1<<n);
    for(int st = 0; st < (1<<n); st++)
    {
        for(int i = 0; i < n; i++)
        {
            if((st>>i)&1)continue;
            for(int j = 0;j < n; j++)
            {
                if(i==j)continue;
                if((st>>j)&1)continue;
                int nst = st|(1<<i)|(1<<j);
                dp[nst] = max(dp[nst],dp[st]+f[i][j]);
            }
        }
    }
    cout<<dp[(1<<n)-1]<<"\n";
    return 0;
}

E - Sandwiches

思路：这个题一开始没整出来。其实做法很简单。

方法一：枚举\(j\)。

对于一个三元组\((i,j,k)\)其中\(A_i=A_k,A_i\neq A_j\)。问有多少满足条件的。

其实很容易想到去枚举\(j\)。

我们用\(idx\)数组存每一种数的下标。对于数\(i\)有\(idx[i].size()\)个。我们去\(for\)每一个。

对于\(idx[i][j-1]\)到\(idx[i][j]\)之间有\(d = idx[i][j]-idx[i][j-1]-1\)个数(都不等于\(i\))，在这一些数的左边有\(j\)个\(i\)（vector下标从0开始的所以是j），右边有\(sz-j\)个\(i\)，这些\(i\)和这\(d\)个数都能构成三元组，方案数是\(j*d*(sz-j)\)

// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 3e5 + 10;
vector<int>idx[N];
ll a[N];
int main()
{
    ios::sync_with_stdio(false);   cin.tie(nullptr), cout.tie(nullptr);
    int n;
    cin>>n;
    for(int i = 1;i <= n; i++)
        cin>>a[i],idx[a[i]].push_back(i);
    ll ans = 0;
    for(int i = 1;i <= n; i++)
    {
        int sz = idx[i].size();
        for(ll j = 1;j < sz; j++)
        {
            ans += j*(idx[i][j]-idx[i][j-1]-1)*(sz-j);
        }
    }
    cout<<ans<<"\n";

    return 0;
}

方法二：扫描线思想

该部分引用自

我们以\(k\)为扫描线，统计在\(k\)左侧的满足条件的三元组。

我们用\(idx\)维护每种数的下标。

图1

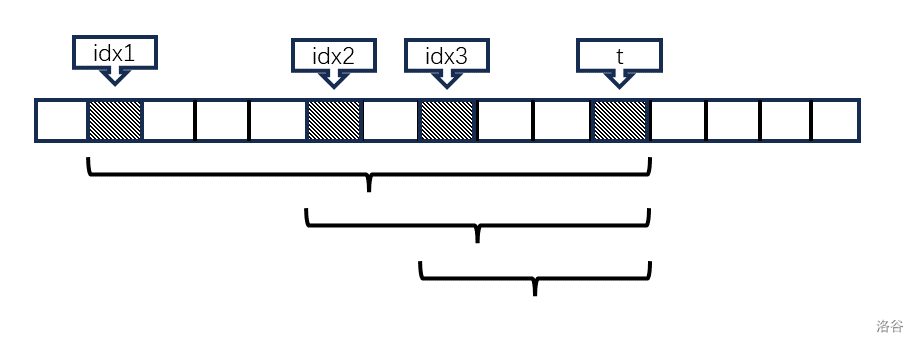
我们令当前扫描线位置是\(t\)，所有在\(t\)左侧且与\(t\)相同的元素的下标是\(idx_i\)。那么除了这些元素其他的元素一定和\(a_t\)不一样。我们统计每个\(idx_i\)到\(t\)之间的贡献：长度-一样的

\(idx_1\)的贡献：\(t-idx_1-1-2\)

\(idx_2\)的贡献：\(t-idx_2-1-1\)

\(idx_3\)的贡献：\(t-idx_1-1-0\)

\(...\)

\(idx_i\)的贡献：\(t-idx_i-1-(m-i)\)(其中m为i的最大编号)

总贡献就是：\(m\times t - \sum_{i = 1}^{m}idx_i-m-\dfrac{(m-1)m}{2} = m(t-1)-\dfrac{(m-1)m}{2}-\sum_{i = 1}^{m}idx_i\)

// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 3e5 + 10;
ll a[N],sumidx[N],cntidx[N];

int main()
{
    ios::sync_with_stdio(false);   cin.tie(nullptr), cout.tie(nullptr);
    int n;
    cin>>n;
    set<int>s;
    for(int i = 1; i <= n; i++)
        cin>>a[i];
    ll ans = 0;
    for(ll i = 1;i <= n; i++)
    {
        ans += cntidx[a[i]]*(i-1)-sumidx[a[i]]-(cntidx[a[i]]-1)*cntidx[a[i]]/2;
        cntidx[a[i]]++;
        sumidx[a[i]]+=i;
    }
    cout<<ans<<"\n";
    return 0;
}

标签：AtCoder,318,const,idx,int,ll,ABCDE,cin,vx
From： https://www.cnblogs.com/nannandbk/p/17723249.html

相关文章

  • AtCoder Beginner Contest 320 ABCDE
    AtCoderBeginnerContest320A-LeylandNumber思路：直接快速幂//AConemoretimes//nndbk#include<bits/stdc++.h>usingnamespacestd;typedeflonglongll;constintmod=1e9+7;constintN=2e5+10;llqmi(lla,llb){llans=1;whil......
  • AtCoder Beginner Contest 253 E
    AtCoderBeginnerContest253E-DistanceSequence思路：前缀和优化DP要求$|a[i]-a[i+1]|>=k\(定于\)dp[i][j]:\(前\)i\(个数以\)j\(结尾的合法序列数列\)dp[i][j]+=dp[i-1][1～(j-k)]+dp[i-1][(j+k)～m]$直接写的话复杂度是\(O(nm^2)\)的会TLE，我们发现可以做一个前缀和优化......
  • AtCoder Beginner Contest 313 Ex Group Photo
    洛谷传送门AtCoder传送门考虑若重排好了\(a\)，如何判断可不可行。显然只用把\(b\)排序，把\(\min(a_{i-1},a_i)\)也排序（定义\(a_0=a_{n+1}=+\infty\)），按顺序逐个判断是否大于即可。这启示我们将\(\min(a_{i-1},a_i)\)排序考虑。考虑从大到小加入\(a_i\)，那么......
  • AtCoder Grand Contest 017
    链接C.SnukeandSpells容易发现合法序列排序后一定是若干段值域连续的部分组成：可以发现最小次数就是重叠/空出的部分大小。每次修改只会对\(O(1)\)个点\(±1\)，直接维护即可。#include<iostream>#include<cstdio>#include<cstring>#include<vector>#defineN200010......
  • AtCoder Grand Contest 023 E Inversions
    洛谷传送门AtCoder传送门首先将\(a\)从小到大排序，设\(p_i\)为排序后的\(a_i\)位于原序列第\(p_i\)个位置，\(x_i\)为要填的排列的第\(i\)个数。设\(A=\prod\limits_{i=1}^n(a_i-i+1)\)，则\(A\)为排列的总方案数（考虑按\(a_i\)从小到大填即得）。套路地，统......
  • Atcoder Regular Contest 165(A~E)
    赛时45min切A~C，降智不会D，罚坐1h，喜提rk70+->rk170+。A-SumequalsLCM可证明结论：若\(N\)只含有一种质因子则无解，否则有解。B-SlidingWindowSort2这么多cornercase的题竟然10min一发入魂，类目了。由于操作是升序排序，且要求最终字典序最大，所以如果存在一个......
  • AtCoder Beginner Contest 320
    A-LeylandNumbera,b=map(int,input().split(''))print(a**b+b**a)B-LongestPalindromes=input()n=len(s)res=0forlinrange(1,n+1):foriinrange(0,n-l):t=q=s[i:i+l]t=t+t[::-1]......
  • [ARC119F] AtCoder Express 3
    题目链接观察样例1的解释，发现切换类型的方法是比较单一的这种就是直接走一段换一段，我们可以人为钦定换乘时最多走一步，因为相邻的同色也可以视作走车站这种情况复杂一些，需要往回走一段，但是依然可以发现往回走也至多一步，因为如果走了两步说明往回走了一步到达的车站依......
  • 【杂题乱写】AtCoder-ARC113
    AtCoder-ARC113AA*B*C枚举\(A,B\)，那么\(C\in[1,\left\lfloor\frac{K}{AB}\right\rfloor]\)，时间复杂度是\(O(K\logK)\)。提交记录：Submission-AtCoderAtCoder-ARC113BA^B^C\(A^k\)的末尾存在循环节，找到循环节长度\(|T|\)，答案就是\(A^{B^C\bmod|T|}\bmod10\)。提......
  • 【题解】AtCoder-ABC320
    AtCoder-ABC320ALeylandNumber依题意计算。提交记录：Submission-AtCoderAtCoder-ABC320BLongestPalindrome直接\(O(n^2)\)枚举，\(O(n)\)判断。提交记录：Submission-AtCoderAtCoder-ABC320CSlotStrategy2(Easy)不妨将字符串复制三遍，枚举\([0,3m)\)判断。提交......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99