树状数组 ( \(\text{fenwick tree}\) ) 是主要用于前缀信息维护的一维数组 ——《信息学奥林匹克辞典》
基础树状数组
维护信息
维护一个数列的元素的操作
可进行的操作
-
单点修改,即修改数列中其中一个元素的值
-
区间查询,即查询数列中连续一段区间的值进行某种运算
存储方法
树状数组的本体是一个数组。
它巧妙地运用了二进制的思想,将树状数组本体中的每一个元素所管辖的范围由其下标决定。
具体地,若设其本体为 \(\text{C++}\) 中的数组 ft,则 ft[i] 所管辖的范围为 \([\) i - lowbit(i) + 1 , i \(]\)
若还不理解的话,可看下面的图:
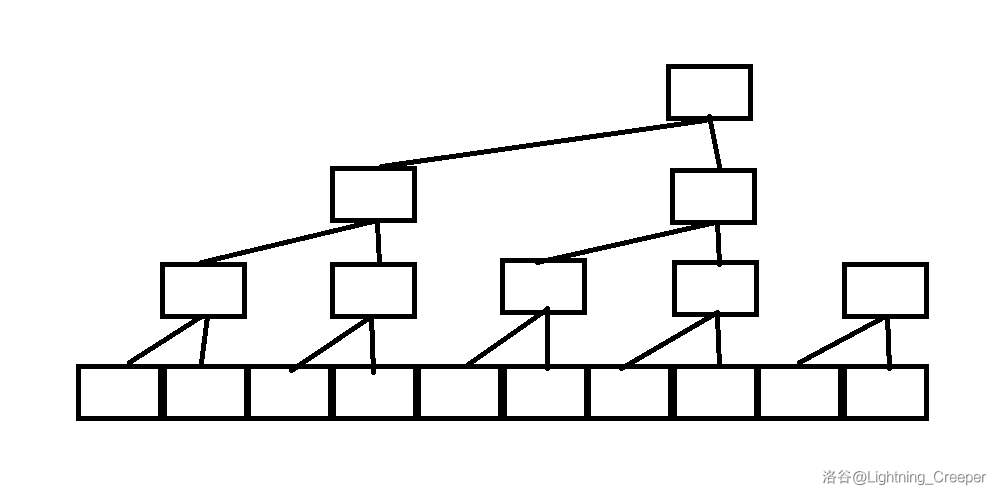
操作方法
单点修改
易发现,修改一个点,只需修改它本身与其祖先即可。
那我们怎么快速得到一个数的父亲节点呢?
既然自己管辖了 lowbit(i) 个,那它的兄弟肯定也管辖了 lowbit(i) 个节点,而我们发现,因为此时我们已经是这一列的最上层了,所以,它的兄弟的下标实际上就是它们父亲的下标!
所以:fa = i + lowbit(i)
又因为它最多有 \(\log n\) 个祖先,所以它时间复杂度为 \(\Theta(\log n)\)
区间查询
我们先思考一个更简单的问题:怎么查询 \(1\) 到 \(x\) 的运算起来的值呢?
由于我们要尽可能地应用我们已知的值,则试图找到一个满足 \(\log_2k\in\mathbb Z 且 k \le n\),此时,我们可以把 ft[k] 的贡献算上,然后问题就转化成了查询 \(k+1\) 到 \(x\) 的运算起来的值,注意到因为 \(\log_2k \in \mathbb Z\),所以可以用 \(1\) 到 \(x\) 的方法来算。
回到原问题,我们就可以用前缀和的思想来解决它了。
容易发现,每计算一次,区间大小都至少会减半,故其时间复杂度为 \(\Theta(\log n)\)。
代码
以加法为例。
int n;
int ft[MAXN];
int lowbit(int x) {
return x & (-x);
}
int sum(int x, int y) {
int s = 0;
for (int i = y; i >= 1; i -= lowbit(i)) {
s += ft[i];
}
for (int i = x - 1; i >= 1; i -= lowbit(i)) {
s -= ft[i];
}
return s;
}
void add(int x, int v) {
for (int i = x; i <= n; i += lowbit(i)) {
ft[i] += v;
}
}
差分+树状数组
可进行的操作
-
区间修改
-
单点查询
操作方法
容易想到使用差分来把它转化成基础树状数组,即用它维护差分数组,然后单点查询变成了区间查询,区间修改变成了单点修改。
代码
int n;
int ft[MAXN];
int lowbit(int x) {
return x & (-x);
}
int sum(int x) {
int s = 0;
for (int i = x; i >= 1; i -= lowbit(i)) {
s += ft[i];
}
return s;
}
void add(int x, int y, int v) {
for (int i = x; i <= n + 1; i += lowbit(i)) {
ft[i] += k;
}
for (int i = y+1; i <= n + 1; i += lowbit(i)) {
ft[i] -= k;
}
}
二维树状数组
维护信息
它所维护的是矩阵内的元素的操作。
可进行的操作
-
单点修改
-
子矩阵查询
存储方法
一个二维数组,所维护的东西简单粗暴地把树状数组里套了个树状数组。
操作方法
实际上也很简单粗暴,就是把每个元素当作一个树状数组再进去操作。
注意,它的时间复杂度为 \(\Theta(\log^2 n)\)。
代码
int n, ft[MAXN][MAXN];
int lowbit(int x) {
return x & (-x);
}
void add(int x, int y, int z) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= n; j += lowbit(j))
ft[i][j] += z;
}
int query(int x, int y) {
int res = 0;
for (int i = x; i >= 1; i -= lowbit(i))
for (int j = y; j >= 1; j -= lowbit(j))
res += ft[i][j];
return res;
}
注
- 文中出现的
lowbit指的是该数在二进制状态下的最后一个 \(1\) 所表示的数,在补码下可用x & (-x)来计算