首页 > 其他分享 >树上散点

树上散点

时间：2023-09-19 16:47:21浏览次数：30  
标签：pre tmp int dep 散点 lca 树上 id

一个博客需要一份头图：

强制在线（论一个 ^ 引起的癫狂：

P6177 Count on a tree II/【模板】树分块

题意：

给定一棵树，每个节点有颜色。

每次询问一条路径上不同颜色的个数，强制在线。

数据范围 \(1 \leq n \leq 4\times 10^4,1\leq m \leq 10^5\)，其中 \(n\) 为点数，\(m\) 为查询数。

考虑在树上随机选 \(k\) 个点作为关键点，使得树上每个点距离其最近的祖先关键点距离不超过 \(\frac{n}{k}\)。

具体地，如果一个点的 \(1 \sim \frac{n}{k}\) 级祖先都不是关键点，则把 \(\frac{n}{k}\) 级祖先标记为关键点。

为方便，最好也取根节点为关键点。

然后预处理出每条路径上，各各关键节点之间的答案，可以用 bitset 维护。

那么最多要处理 \(k^2\) 个点之间的答案，预处理复杂度为 \(O(\frac{nk^2}{w})\)。

具体地，只需要用栈维护当前路径的节点即可。

下面考虑如何处理询问。可以把一个询问拆成这样：

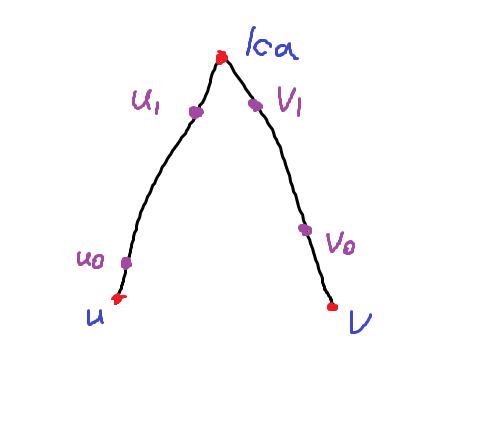
其中紫色为关键节点。

那么对于红色点与紫色点之间，则暴力跳，对于紫色点之间则用之前预处理出的答案。

对于从 \(u_0 \rightarrow u_1\)，只需要记录下每个关键点在树链上的上一个关键点 \(lst\) 即可。

还要注意空间复杂度，这里取 \(k=80\)。

#include<bits/stdc++.h>
using namespace std;

const int N=4e4+5;
int n,m,q,top,ans,a[N],lsh[N],lst[N];
int tot,id[N],dis[N],dep[N],f[N][16],stk[N];
bitset<N> t[82][82],tmp;
vector<int> G[N];

int rd()
{
    int x=0;char c=getchar();
    for(;!isdigit(c);c=getchar());
    for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^48);
    return x;
}

void dfs(int u,int fa)
{
    dis[u]=dep[u]=dep[fa]+1,f[u][0]=fa;
    for(int i=1;i<=15;i++) f[u][i]=f[f[u][i-1]][i-1];
    for(int v:G[u])
    {
        if(v==fa) continue;
        dfs(v,u);
        dis[u]=max(dis[u],dis[v]);
    }
    if(dis[u]-dep[u]>=500) dis[u]=dep[u],id[u]=++tot;
}

void dfs2(int u)
{
    for(int v:G[u])
    {
        if(v==f[u][0]) continue;
        if(id[v])
        {
            int x=id[stk[top]],y=id[v];
            for(int i=v;i!=stk[top];i=f[i][0]) t[x][y].set(a[i]);
            tmp=t[x][y];
            for(int i=1;i<top;i++) t[id[stk[i]]][y]=t[id[stk[i]]][x]|tmp;
            lst[v]=stk[top];
            stk[++top]=v;
        }
        dfs2(v);
        if(id[v]) top--;
    }
}

int getlca(int u,int v)
{
    if(dep[u]<dep[v]) swap(u,v);
    for(int i=15;~i;i--) if(dep[f[u][i]]>=dep[v]) u=f[u][i];
    if(u==v) return u;
    for(int i=15;~i;i--) if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
    return f[u][0];
}

void work(int u,int lca)
{
    int pre=u;
    while(dep[lst[pre]]>=dep[lca]) pre=lst[pre];
    if(pre!=u) tmp|=t[id[pre]][id[u]];
    while(pre!=lca) tmp.set(a[pre]),pre=f[pre][0];
}

int main()
{
    n=rd(),q=rd();
    for(int i=1;i<=n;i++) a[i]=lsh[i]=rd();
    sort(lsh+1,lsh+1+n);
    m=unique(lsh+1,lsh+1+n)-lsh-1;
    for(int i=1;i<=n;i++) a[i]=lower_bound(lsh+1,lsh+1+m,a[i])-lsh;
    for(int i=1;i<n;i++)
    {
        int u=rd(),v=rd();
        G[u].push_back(v),G[v].push_back(u);
    }
    dfs(1,0);
    if(!id[1]) id[1]=++tot;
    stk[++top]=1;
    dfs2(1);
    while(q--)
    {
        int u=rd()^ans,v=rd(),lca=getlca(u,v);
        tmp.reset();
        while(u!=lca&&!id[u]) tmp.set(a[u]),u=f[u][0];
        while(v!=lca&&!id[v]) tmp.set(a[v]),v=f[v][0];
        tmp.set(a[lca]);
        if(u!=lca) work(u,lca);
        if(v!=lca) work(v,lca);
        printf("%d\n",ans=tmp.count());
    }
}

三倍经验：

SP10707

雪辉

雪辉这道题还有求个 mex，只需要把 bitset 取反后求 lowbit 即可，bitset 有个函数叫 _Find_first()

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+5;
int n,q,totE,top,ans,op,a[N],lst[N];
int tot,id[N],dis[N],dep[N],f[N][20],stk[N];
bitset<30005> t[155][155],tmp;
int pre[N],nxt[N<<1],to[N<<1];
void add(int u,int v){to[++totE]=v,nxt[totE]=pre[u],pre[u]=totE;}

int rd()
{
    int x=0;char c=getchar();
    for(;!isdigit(c);c=getchar());
    for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^48);
    return x;
}

void dfs(int u,int fa)
{
    dis[u]=dep[u]=dep[fa]+1,f[u][0]=fa;
    for(int i=1;i<18;i++) f[u][i]=f[f[u][i-1]][i-1];
    for(int i=pre[u];i;i=nxt[i])
    {
        int v=to[i];
        if(v==fa) continue;
        dfs(v,u);
        dis[u]=max(dis[u],dis[v]);
    }
    if(dis[u]-dep[u]>=1000) dis[u]=dep[u],id[u]=++tot;
}

void dfs2(int u)
{
    for(int i=pre[u];i;i=nxt[i])
    {
        int v=to[i];
        if(v==f[u][0]) continue;
        if(id[v])
        {
            int x=id[stk[top]],y=id[v];
            for(int i=v;i!=stk[top];i=f[i][0]) t[x][y].set(a[i]);
            tmp=t[x][y];
            for(int i=1;i<top;i++) t[id[stk[i]]][y]=t[id[stk[i]]][x]|tmp;
            lst[v]=stk[top];
            stk[++top]=v;
        }
        dfs2(v);
        if(id[v]) top--;
    }
}

int getlca(int u,int v)
{
    if(dep[u]<dep[v]) swap(u,v);
    for(int i=17;~i;i--) if(dep[f[u][i]]>=dep[v]) u=f[u][i];
    if(u==v) return u;
    for(int i=17;~i;i--) if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
    return f[u][0];
}

void work(int u,int lca)
{
    int pre=u;
    while(dep[lst[pre]]>=dep[lca]) pre=lst[pre];
    if(pre!=u) tmp|=t[id[pre]][id[u]];
    while(pre!=lca) tmp.set(a[pre]),pre=f[pre][0];
}

void get(int u,int v)
{
    int lca=getlca(u,v);
    while(u!=lca&&!id[u]) tmp.set(a[u]),u=f[u][0];
    while(v!=lca&&!id[v]) tmp.set(a[v]),v=f[v][0];
    tmp.set(a[lca]);
    if(u!=lca) work(u,lca);
    if(v!=lca) work(v,lca);
}

int main()
{
    n=rd(),q=rd(),op=rd();
    for(int i=1;i<=n;i++) a[i]=rd();
    for(int i=1;i<n;i++)
    {
        int u=rd(),v=rd();
        add(u,v),add(v,u);
    }
    dfs(1,0);
    if(!id[1]) id[1]=++tot;
    stk[++top]=1;
    dfs2(1);
    while(q--)
    {
        int cnt=rd();tmp.reset();
        for(int i=1;i<=cnt;i++) get(rd()^ans,rd()^ans);
        int a1=tmp.count();tmp=~tmp;
        int a2=tmp._Find_first();
        printf("%d %d\n",a1,a2);
        if(op) ans=(a1+a2);
    }
}

标签：pre,tmp,int,dep,散点,lca,树上,id
From： https://www.cnblogs.com/spider-oyster/p/17715050.html

相关文章

  • 散点图
    散点图点击查看代码importmatplotlib.pyplotaspltimportpandasaspdimportmatplotlibplt.rcParams["font.sans-serif"]=["SimHei"]#解决英文冲突问题matplotlib.use('TkAgg')x=[1,2,3,4,5,6]y=[19,29,39,22,33,49]plt.scatt......
  • 【LuoGu】3047 Nearby Cows G ——两次DFS+树上DP
    [USACO12FEB]NearbyCowsG题目描述给你一棵\(n\)个点的树，点带权，对于每个节点求出距离它不超过\(k\)的所有节点权值和\(m_i\)。输入格式第一行两个正整数\(n,k\)。接下来\(n-1\)行，每行两个正整数\(u,v\)，表示\(u,v\)之间有一条边。最后\(n\)行，每行一个非负整数......
  • 【LuoGu】2014 选课——树上DP
    [CTSC1997]选课题目描述在大学里每个学生，为了达到一定的学分，必须从很多课程里选择一些课程来学习，在课程里有些课程必须在某些课程之前学习，如高等数学总是在其它课程之前学习。现在有\(N\)门功课，每门课有个学分，每门课有一门或没有直接先修课（若课程a是课程b的先修课即只有......
  • 树上差分
    树上差分与线性差分差不多，只不过是在树上进行差分，每次将两个点x和y的标志加1，将lca(x,y)和fa(lca(x,y))的标志减1，最后来一次深搜求和，就可以得到值了下面给出几道例题1.P3128[USACO15DEC]MaxFlowP解析：树上差分板子题，直接套班子，求完值后，求最大值即可代码：#include<bits/std......
  • UOJ33 树上 GCD
    UOJ传送门设\(f_{u,i}\)为\(u\)子树内深度为\(i\)的点的个数，在\(\operatorname{LCA}\)处计算答案。但是时间复杂度无法接受。考虑长剖，计算答案只用枚举到轻链长，先对轻儿子做一遍\(\text{Dirichlet}\)后缀和，重儿子的信息直接继承上来。但是我们没法查询深度\(\bmod......
  • 第 360 场周赛 （二进制枚举、树上倍增）
    2833. 距离原点最远的点 本题要求最远的距离，所有‘_’必须全为左或全为右。利用前缀和的思想看看L多还是R多，最后加上_的数目就是答案。classSolution{public:intfurthestDistanceFromOrigin(stringmoves){intn=moves.size();inttt=0,l......
  • 绘制矩阵散点图
    什么是矩阵散点图当我们想要探索两组变量之间的关系时，矩阵散点图是一种有用的可视化工具。它能够帮助我们快速地观察多个变量之间的关联性，特别是在统计分析和数据挖掘领域中。矩阵散点图实际上是由多个散点图组成的矩阵，每个散点图表示两个不同变量之间的关系。绘制矩阵散点图......
  • 2023牛客暑期多校练营6 A-Tree 树上背包+并查集
    2023牛客暑期多校练营6A-Tree树上背包+并查集题目链接题意：给出一棵树，节点为黑色或者白色，定义整棵树的贡献为，任意白点到任意黑点所经过路径上的最大边权之和，节点i原本颜色已给出，可以花费c[i]代价翻转节点i的颜色，问最大贡献是多少。做法：首先我们思考怎么处理最大边权的问题......
  • 树上可持久化线段树
    例题传送门：Countonatree简要题意：有棵\(n\)个节点的树，每次点有个权值\(a_i\)，每次询问给出\(u,v,k\)，求\(u,v\)两个节点的简单路径上(包括\(u,v\))上第\(k\)小的点，保证数据有解，强制在线\(1\len,m\le10^5,a_i\in[1,2^{31}-1]\)首先，第\(k\)小就可以想到要可持久化线段树，动态开......
  • 树上启发式合并
    与其说树上启发式合并是一种算法，不如说是一种思想。它在于通过”小的并入大的“保证复杂度，从而解决很多看似无法做的问题。论纯用树上启发式合并的题很少，但是很多题却可以用树上启发式合并去解决。模板求解的问题往往具有如下性质：每颗子树都有要记录的信息，信息的数量和子树大......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99