洛谷 \(P1862\) 输油管道问题
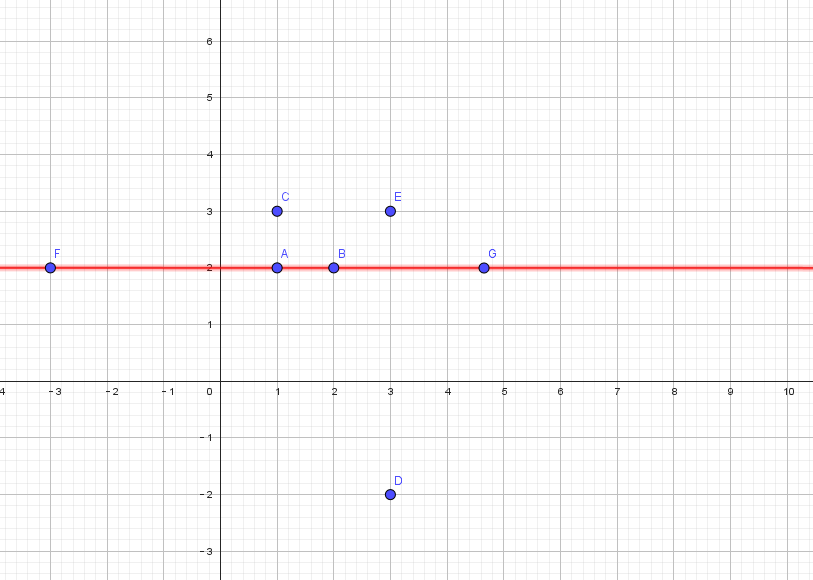
如果只有一口井,那么显然是越近越好。如果有两口井,那么显然是有以下三种情况:
-
两口井都在主管道北边,那么这个时候的两个连接管道的长度和肯定大于两口井的\(Y\)坐标之差。
-
两口井都在主管道南边,和情况1是一样的
-
两口井,一个在主管道南边,一个在主管道北边,那么两个连接管道的长度和就等于两口井的\(Y\)坐标之差。
显然情况三是所要的最短管道的设计情况。就是当主管道在两口井之间的任意位置时,连接管道长度之和都等于两口井的\(Y\)坐标之差,是最短的长度。
那么将这个结论推广,当有\(n\)口井的时候,
-
\(n\)是偶数 只要这\(n\)口井分布在主管道的两边,一边\(n/2\)个,那么就是距离之和最小的。
-
\(n\)是奇数,只要将这\(n\)个井中,\(Y\)坐标最中间的(也就是\(Y\)是中值的那个)井不算,其余的偶数个井分布在主管道的两侧,这个时候移动主管道,那么这\(n\)个连接管道长度之和就决定于那个没有算的井了,因为其余的井的距离之和是固定了的,这个时候只要主管道最接近那个点就好了。
也就是说,输油管道的位置就是最中间的那口井(或中间的区间)。我的方法是将各口井的\(y\)坐标排序(\(x\)坐标不用管),再取 \(n\) \(div\) \(2\)+\(1\) 的位置,即最中间的位置。
#include <bits/stdc++.h>
using namespace std;
const int N = 10005;
/*
文件名:petroleum
题目:洛谷 P1862 输油管道问题
题目网址:https://www.luogu.com.cn/problem/P1862
输入:
5
1 2
2 2
1 3
3 -2
3 3
输出:
6
*/
int n, a[N]; // a[0..n-1]。第i口油井的纵坐标在a[i]
int main() {
// 输入数据
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i] >> a[i]; // 横坐标说没有用的,可以直接抛弃掉
// 排序
sort(a, a + n);
// 两端对称取长短。中位数原理。
int sum = 0;
for (int i = 0, j = n - 1; i <= j; i++, j--) sum += a[j] - a[i];
cout << sum << endl;
return 0;
}