由于 \(A_{i,j}=a_ib_j\),这个 \(f(B)\) 显然可以化简:
\[\begin{aligned}f(B)&=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^t\sum\limits_{k=\min(B_{i,j},B_{i+1,j})}^{\max(B_{i,j},B_{i+1,j})}A_{i,k}\\&=\sum\limits_{i=1}^n\sum\limits_{j=1}^t\sum\limits_{k=\min(B_{i,j},B_{i+1,j})}^{\max(B_{i,j},B_{i+1,j})}a_ib_k\\&=\sum\limits_{i=1}^na_i\sum\limits_{j=1}^tS_{\max(B_{i,j},B_{i+1,j})}-S_{\min(B_{i,j},B_{i+1,j})-1}\end{aligned} \]\(S_i\) 为 \(b\) 数组的前缀和。
发现若得到 \(g(B_1,B_2)=\sum\limits_{j=1}^tS_{\max(B_{1,j},B_{2,j})}-S_{\min(B_{1,j},B_{2,j})-1}\) 的最小值,我们可以令 \(B_{2k+1}=B_1,B_{2k+2=N_2}\)。这样显然最优。也就是说,\(f(B)=\left(\sum\limits_{i=1}^na_i\right)\cdot \min g(B_1,B_2)\)。
问题转换为找到一个 \(B_1,B_2\),分别满足每个元素两两不同,都在 \([1,m]\) 之间,并且对应的位置上的元素不同,使得 \(g(B_1,B_2)\) 最小。
由于同一行元素两两不同以及值域的限制,考虑进行匹配。相当于现在有两列数(分为左部和右部),分别为 \(1,2,\cdots ,m\),在左部中选择 \(t\) 个数,并和右部的 \(t\) 个数匹配。满足不存在形如 \((i,i)\) 的匹配,一对匹配 \((i,j)\) 的价值就是 \(S_{\max(i,j)}-S_{\min(i,j)-1}\),也就是 \(b_{\min(i,j)}+b_{\min(i,j)+1}+\cdots+b_{\max(i,j)}\)。一组匹配的价值就是每对匹配的价值之和,求钦定有 \(t\) 对匹配的最小匹配。
有个比较感性的想法,就是一对匹配不应该跨过太大的距离。考虑从左到右按顺序匹配,如果匹配跨过了一段空区间,那么不如不跨过这段区间,因为这样减小了代价的同时也给后面的点更多的选择方案。
另一个比较感性的想法,匹配应该尽可能不交叉。这里借用这篇题解的图:
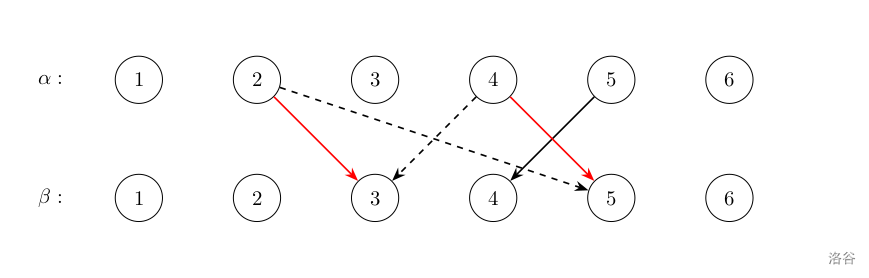
如上图,匹配 \((2,5)(4,3)\) 显然不如匹配 \((2,3),(4,5)\)。即如果存在交叉的匹配,我们尝试交换匹配以减少价值。
最终只剩下三种结构:连续的三元环,例如 \((i,i+1)(i+1,i+2)(i+2,i)\) ;连续的二元环,例如 \((i,i+1)(i+1,i)\);连续的一条链,例如 \((i,i+1)(i+1,i+2)(i+2,i+3)\cdots (i+k,i+k+1)\)。前两种情况有交叉,但是无法调整;并且能够发现,只有前两种情况无法调整。
然后就能考虑 dp 了:令 \(f_{i,j,0/1}\) 表示目前考虑到 \(i\) 的匹配 \((i,?)\),前 \(i\) 个点一共有 \(j\) 对匹配,目前是否在一条形如 \((u,u+1)(u+1,u+2)\cdots(i-1,i)\) 的链中。
- \(f_{i,j,1}\gets f_{i-1,j-1,1}+b_{i}+b_{i-1}\),表示延续一条链,增加一对匹配,连接 \((i-1,i)\)。
- \(f_{i,j,1}\gets f_{i-2,j-1,0}+b_i+b_{i-1}\),表示新建一条链,增加一对匹配,连接 \((i-1,i)\)。
- \(f_{i,j,0}\gets f_{i-2,j-2,0}+2(b_i+b_{i-1})\),表示新增一个二元环,增加两对匹配,连接 \((i-1,i)(i,i-1)\)。
- \(f_{i,j,0}\gets f_{i-3,j-3,0}+2b_i+3b_{i-1}+2b_{i-2}\),表示新增一个三元环,增加三对匹配,连接 \((i-2,i-1)(i-1,i)(i,i-2)\) 或者 \((i,i-1)(i-1,i-2),(i-2,i)\)。
- \(f_{i,j,0}\gets f_{i-1,j,0}\),表示 \(i\) 没有匹配任何点。
- \(f_{i,j,0}\gets f_{i,j,1}\),表示我摆烂了,不延续一条链。
乍一看是 \(O(mt)\) 的?的确是 \(O(mt)\) 的。
考虑瓶颈在于强制选择 \(t\) 对匹配,对于这类问题,我们可以通过证明答案随匹配数的变化具有凸性,而进行 wqs 二分。
这题的凸性十分显然,因为是匹配问题,可以转化成费用流模型:
- 有超源 \(S'\) 和超汇 \(T'\),源点 \(S\) 和汇点 \(T\),\(S'\to S\) 连流量 \(t\),费用 \(0\) 的边(以下 \(u\to v\) 连流量 \(f\) 费用 \(w\) 的边简记为 \(u\to v(f,w)\))。即 \(S'\to S(t,0),T\to T'(t,0)\)。
- 记 \(i\) 的左部点为 \(l_i\),右部点为 \(r_i\),\(S\to l_i(1,0),r_i\to T(1,0)\)。
- 对于 \(i\neq j\),\(l_i\to r_i(1,S_{\max(i,j)}-S_{\min(i,j)-1})\)。
不难发现最小费用最大流就是答案。根据费用流函数的凸性,原问题具有凸性,可以 wqs 二分。具体地,二分斜率 \(k\),新建一对匹配时,直接减去 \(k\) 的代价即可。
最终复杂度 \(O(n\log V)\)。
标签:彼世,匹配,limits,min,P8544,Wdoi,sum,max,gets From: https://www.cnblogs.com/Ender32k/p/17713788.html