标签：结点应用题元素存储 next 二叉树数据结构节点

数据结构应用题考点

数组

数组的存储结构

一维数组

A[0...n-1]为例，存储关系

\[LOC(ai)=LOC(a0)+(i)×L(0≤i＜n) \]

L是每个数组元素所占存储单元

多维数组

对于多维数组，有两种映射方法：按行优先和按列优先。

以二维数组为例，按行优先存储的基本思想是：先行后列。
先存储行号较小的元素，行号相等先存储列号较小的元素。
设二维数组行下标与列下标的范围分别为

\[[l1,h1],[l2,h2] \]

，则存储结构关系式为：

\[LOC(a i,j )=LOC(a l 1 ,l 2 )+[(i−l 1 )×(h 2 −l 2 +1)+(j−l 2 )]×L \]

若l1 l2均为0，则上式变成

\[LOC(a i,j )=LOC(a 0,0 )+[i×(h 2 +1)+j)]×L \]

矩阵压缩存储

压缩存储：指为多个值相同的元素只分配一个存储空间，对零元素不分配存储空间。其目的是为了节省存储空间。

特殊矩阵：指具有许多相同矩阵元素或零元素，并且这些相同矩阵元素或零元素的分布有一定规律性的矩阵。常见的特殊矩阵有对称矩阵、上（下）三角矩阵、对角矩阵等。

对称矩阵

任意一个n阶方阵A的任意元素aij=aji,则称为一个对称矩阵。
对于n nn阶方阵，其中的元素可以划分为3个部分，即上三角区、主对角线和下三角区。
对称矩阵上下三角区元素相同，因此存放在一维数组

\[B[n(n+1)/2] \]

中，及aij存放在bk中，只存放主对角线和下三角区（或上三角区）

采用行优先存储，存放主对角线和下三角区在这里插入图片描述

若数组下标从0开始，则在数组B中的下标为

\[k=1+2+3+...+(i-1)+(j-1)=i(i-1)/2+j-1 \]

因此元素下标对应关系

若存放主对角线和上三角区

在这里插入图片描述

\[k = n + ( n − 1 ) + . . . + ( n − i + 2 ) + ( j − i ) = ( i − 1 ) ( 2 n − i + 2 ) / 2 + j − i \]

三角矩阵

除了对角线外和上/下三角区，其余的元素都相同

压缩策略：按行优先原则，将三角区和主对角线元素存入一维数组，并在最后一个位置存放常量C

下三角：

上三角：

三对角矩阵

\[∣i−j∣>1时，有Aij=0,呈带状 \]

存储策略：只存储主对角线及其上、下两侧次对角线上的元素外，其他零元素一律不存储。

需要用一个一维数组B 来存储三对角矩阵中位于三对角线上的元素。同样要区分两种存储方式：即行优先方式和列优先方式。

行优先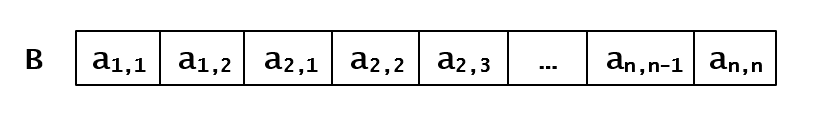：在这里插入图片描述

那么数组B中，位于Aij（i<=j)，前边的元素个数为

\[k = 2 + 3 ( i − 2 ) + j − i + 1 = 2 i + j − 3 （数组下标从0开始） \]

于是有对于i的求法，详细如下

\[\begin{align} &前i-1行有3(i-1)+1个元素\\ &前i行共有3i-1个元素\\ &B数组下标为k的元素是第k+1个\\ &3(i-1)+1<k+1<=3i-1\\ &即3(i-1)+1<=k<3i-1\\ &i=⌊(k+1)/3+1⌋ \end{align} \]

栈、队列

数据结构定义

顺序表

用一组地址连续的存储单元依次存储线性表中的数据元素，逻辑上相邻的物理位置上也相邻

顺序表的实现

静态分配实现顺序表

#include <stdio.h>
#define MaxSize 10
//结构定义
Typedef struct {
    ElemType data[MaxSize];
    int length;
}SqList;
//实现顺序表
void InitList(Sqlist &L){
    int i;
    for(i=0;i<MaxSize;i++)
        L.data[i]=0;   //防止脏数据
    L.length=0;
}

动态分配实现顺序表

#include <stdio.h>  //用到malloc和free函数
#define InitSize 10
typedef struct{
    int *data;//定义数据元素的类型为int型
    int Maxsize;
    int length;
}Seqlist
 //初始化
void InitList(Seqlist &L){
    L.data=(int *)malloc(InitSize*sizeof(int));
    L.length=0；
    L.MaxSize=InitSize;
}
 //申请新的空间
void IncreaseSize(Seqlist &L, int len){
    int *p=L.data;
    L.data=(int *)malloc((L.MaxSize+len)sizeof(int)); //申请一块新空间
    for(int i=0;i<l.length;i++){
        L.data[i]=p[i];        //将数据复制到新区域
    }
    L.MaxSize=L.MaxSize+len;
    free(p);  //释放原来的内存空间，p也会被自动收回
}

单链表

单链表指线性表的链式存储，用一组任意的存储单元来存储数据元素；
而为了建立元素之间的线性关系，对每个链表结点，还要存放一个指向后继的指针；
头指针用以标识单链表，如果其值为 NULL，说明为一个空表；
在第一个结点前附加一个结点，成为头结点，可以不记录信息，也可以记录表长。设置头结点，便于空表与非空表的统一处理。

单链表的基本操作

建表：
头插法：将存有读入数据的新结点插入到当前链表表头，使用头插法会导致读入数据与生成链表顺序相反

//核心代码
s->next=head;
head=s;

尾插法：增加一个尾指针，以使新结点直接插入到表尾。

//核心代码
r->next=s;
r=r->next;

查找o(n)：
按序号查找
按值查找

插入结点o(n):
后插操作

p=GetElem(L,i-1);//查找插入位置前驱
s->next=p->next;//1操作
p->next=s;//2操作

删除结点o(n)

p=GetElem(L,i-1);
q=p->next;
p->next=q->next;
free(q);

求表长o(n)

双链表

在单链表基础上增加前驱指针。

双链表的插入：

//1 2步必须在3 4步之前
s->next=p->next;
p->next->prior=s;
s->prior=p;
p->next=s;

双链表的删除

p->next=q->next;
q->next->prior=p;
free(q);

循环链表

对于循环单链表，尾结点指针不是指向 NULL，而是头结点；
对于循环双链表，在循环单链表基础上，头结点的前驱指针指向尾结点

L->next==L;//判空

循环双链表

L->next==L;
L->prior==L;//判空

顺序栈

顺序栈：利用一组地址连续的存储单元存放自栈底到栈顶的元素，同时附设一个指针（top)指示当前栈顶元素的位置

typedef struct{
Elemtype data[MaxSize];
int top;
}SqStack
/*初始设置S.top=-1
栈空：S.top==-1	栈满：S.top==MaxSize-1	栈长：S.top+1

顺序队列

/*q.front==q.rear==0;队空
进队：先入队，然后尾指针加1
出队：先取队头值，然后头指针加1
不能用q.front==MaxSize判断队满（假溢出）*/

循环队列

将存储队列的元素的表从逻辑上视为一个环，称为循环队列

/*初始：q.front=q.rear=0;
队首指针进1：q.front=(q.front+1)%MaxSize;
队尾指针进1:q.rear=(q.rear+1)%MaxSize;
队列长度：(q.rear-q.front+MaxSize)%MaxSize;
牺牲一个单元来区分队满和队空：队满条件(q.rear+1)%MaxSize==q.front;
*/

栈的链式存储

没有头结点的单向链表：

队列的链式存储

/*
q.front==NULL&&q.rear==NULL;队空
*/

树

关于性质的计算、推导

树的性质

树中结点数等于所有结点的度数+1
每个结点的度数 = 孩子结点的个数，最后再加上根结点，就是树中的结点数了
度为m的树中，第i层的结点数至多为m^i-1

\[\begin{align} &证明如下\\ &第 i 层上的结点数 = 第 i-1 层结点的度数*m\\ &也就是m*(i-1层结点数)=m*m*(i-2层结点数)=...=m^{i-1}*第一层结点数即1 \end{align} \]
高度为h的m叉树至多有（m^h-1)/(m-1)个结点

\[S=1*m*m^2*m^3*...*m^{h-1}=(m^h-1)/(m-1) \]
高度为h的m叉树至少有h个结点；高度为h，度为m的树至少有h+m-1个结点

高度为h的m叉树不见得度为m，只是它强调每个结点的度最大为m，因此当它高度为m时允许每个结点度为h，这样串成一串下来，这时它的结点是最少的，此时除了叶子结点外每一个结点的度为1。
度为m的树则又多加了一个限制：至少有一个结点度为m，这时我们可以在高度为h的m叉树的基础上再多增加几个结点使其度数增加到m，由于高度是h已经限定死了，我们不能在叶子结点上增加，这样会导致h增加，因此我们只能再额外增加m-1个，使得某一个非叶子结点的度从1增加到m。
具有n个结点的m叉树的最小高度为⌈log_m(n(m-1)+1)⌉
求最小高度也就是每层结点数最多时的高度，即该树是一棵完全m叉树，设其高度为h。

\[n<=(m^h-1)/(m-1)\\ h>=log_m(n(m-1)+1)\\ 故h为⌈log_m(n(m-1)+1)⌉\\ 另外，实际上有 (m^{h-1}-1)/(m-1) +1≤ n ≤ (m^h-1)/(m-1)，\\故最小高度h也可以为 ⌊log_m((n-1)(m-1)+1)⌋ + 1。 \]
度为m的树和m叉树的区别

度为m的树	m叉树
任意结点度数最多等于m	任意结点度数最多等于m
至少有一个结点的度等于m	允许所有结点的度都小于m
不允许为空树	可以为空树

二叉树的性质

非空二叉树上的叶子结点数等于度为2的结点数加1，即n₀=n₂+1

\[\begin{align} &设度为0，1，2的结点个数分别为n_0,n_1,n_2,设B为分支总数\\ &结点总数n=n_1+n_2+n_0\\ &分支总数B=n_1+2n_2=n+1\\ &n_1+n_2+n_0=n_1+2n_2+1\\ &n_0=n_2+1 \end{align} \]
非空二叉树上第k层至多有2^k-1个结点（k>=1)
高度为h的二叉树至多有2^h-1个结点（h>=1)
对完全二叉树从上到下，从左到右依次编号0，1，2...n,左孩子为2i,右孩子为2i+1,父亲为

\[\lfloor i/2 \rfloor \]

结点i所在的层次（深度）为

\[\lfloor log_2n\rfloor+1 \]

具有n个结点的完全二叉树的高度为

\[\lfloor log_2n \rfloor+1 或者\lceil log_2(n+1) \rceil \]
\[\\ 计算： 2^{h-1}-1<n<=2^{h}-1或者2^{h-1}<=n<2^h \]

数据结构Struct定义

二叉树的顺序存储

二叉树的链式存储

结构体

typedef struct BiTNode{
ElemType data;//数据域
struct BiTNode *lchild,*rchild;//左右孩子
}BiTNode,*BiTree;

在有n个元素的二叉链表中，含有n+1个空链域

多叉树、森林的存储

双亲表示法

用一组连续空间存储每个结点，同时在每个结点中增设一个伪指针，指示其双亲结点在数组的位置，根节点下标为0，伪指针域为-1.

孩子表示法

将每个结点的孩子节点都用单链表连接起来形成一个线性结构，n个结点就有n个孩子链表

孩子兄弟表示法

又称二叉树表示法，以二叉链表作为存储结构，每个结点包括三部分：结点值、指向结点的第一个孩子结点的指针，指向结点下一个兄弟结点的指针。

树的应用

哈夫曼树

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

哈夫曼树又称最优树

哈夫曼树的构造：

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：

(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；

(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；

(3)从森林中删除选取的两棵树，并将新树加入森林；

(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

要求手绘、文字描述建树过程

查找哈夫曼树（译码）

先统计各个结点出现的频率（权值）然后建树，左路经为0，右路径为1，进行编码

哈夫曼编码不会出现相同的前缀

并查集

将元素划分为互不相交的树，表示多个集合

基本操作：
查：从指定元素出发，一路向北找到根节点
并：两个集合合并为一个集合，让其中一个树的根节点连接到另一个树的根节点作为孩子节点

存储结构：双亲表示法

代码实现

初始化：

并、查：

并的时间复杂度o(1),查的时间复杂度为o(n)

优化：在每次union创建树时，小树合并进大树
用根节点的绝对值表示树的结点总数，小树合并进大树

该方法构建的树高不超过

\[\lfloor log_2n \rfloor+1 \]

优化后的Find时间复杂度为O(log₂n)

进一步优化（压缩路径）：Find操作，先找到根节点，再将查找路径上的所有节点都挂到根节点
下

可将Find函数的时间复杂度进一步降低

二叉排序树、平衡二叉树

二叉排序树（BST）：

若它的左子树不为空，则左子树上所有结点的值均小于它根节点的值
若它的右子树不为空，则右子树上所有结点的值均大于它根节点的值
它的左右子树也分别为二叉排序树

查找、插入、构建、删除比较简单，不多赘述

平衡二叉树：

左右子树深度之差的绝对值不超过1;
左右子树仍然为平衡二叉树.

平衡二叉树的调整：

左旋：

当前操作节点是66 （66这个节点是最小失衡树的根节点)
断开该节点的右孩子连接线 (此时变成了两棵树，设以66为根节点的树为原根树，以77为根节点的树为新根树)
判断新根树的根节点的左子树是否为空
- 若空，直接把原根树作为新根树的左子树。
- 若不空:
  - 将新根树的根节点的左子树独立出来，设其名为新原独树。
    把新原独树作为原根树的右子树。
    把原根树作为新根树的左子树。

右旋：

当前操作节点是A （A这个节点是最小失衡树的根节点)
断开该节点的根节点的左孩子连接线 (此时变成了两棵树，设以A为根节点的树为原根树，以B为根节点的树为新根树)
判断新根树的根节点的右子树是否为空
- 若空，直接把原根树作为新根树的右子树。
- 若不空:
  - 将新根树的根节点的右子树独立出来，设其名为新原独树。
    把新原独树作为原根树的左子树。
    把原根树作为新根树的右子树。

四种调整方式

LL 对最小失衡根节点进行一次右旋
RR 对最小失衡根节点进行一次左旋
LR

对最小失衡树的根节点的左孩子(节点B)实行一次左旋，得到下图，

再对最小失衡树的根节点（节点A）（！！！当前的最小失衡树概念基于最初的树，不是已经经过左旋的树！！！)实行一次右旋，成功恢复平衡。
RL

对最小失衡树的根节点的右孩子(节点C)实行一次右旋，得到下图

再对最小失衡树的根节点（（节点A）（！！！当前的最小失衡树概念基于最初的树，不是已经经过右旋的树！！！)）实行一次左旋，成功恢复平衡。

标签：结点,应用题,元素,存储,next,二叉树,数据结构,节点
From： https://www.cnblogs.com/cs-gzh/p/16750950.html

数据结构应用题