description
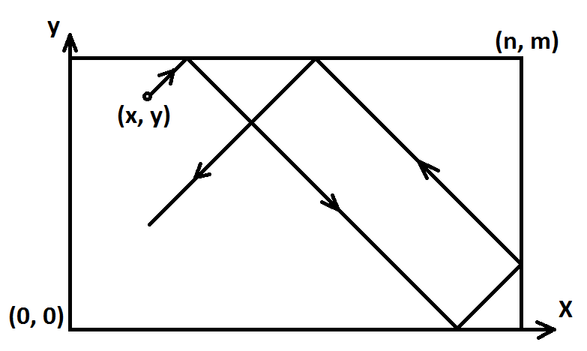
如上图,\((0,0),(0,m),(n,0),(n,m)\) 是四个口袋。一个台球从整点 \((x,y)\) 按照给定的初始方向出发(方向只可能平行于坐标轴或和坐标轴呈 45° 夹角),当它和一个口袋的坐标重合时游戏结束。
给定 \(n,m,x,y\) 以及球初始的速度方向,求它最终落到哪个口袋。
如果不可能落进任何一个口袋输出 -1。
solution
根据 初中物理的 光学知识可知,可以用如下方式描述台球的运动:
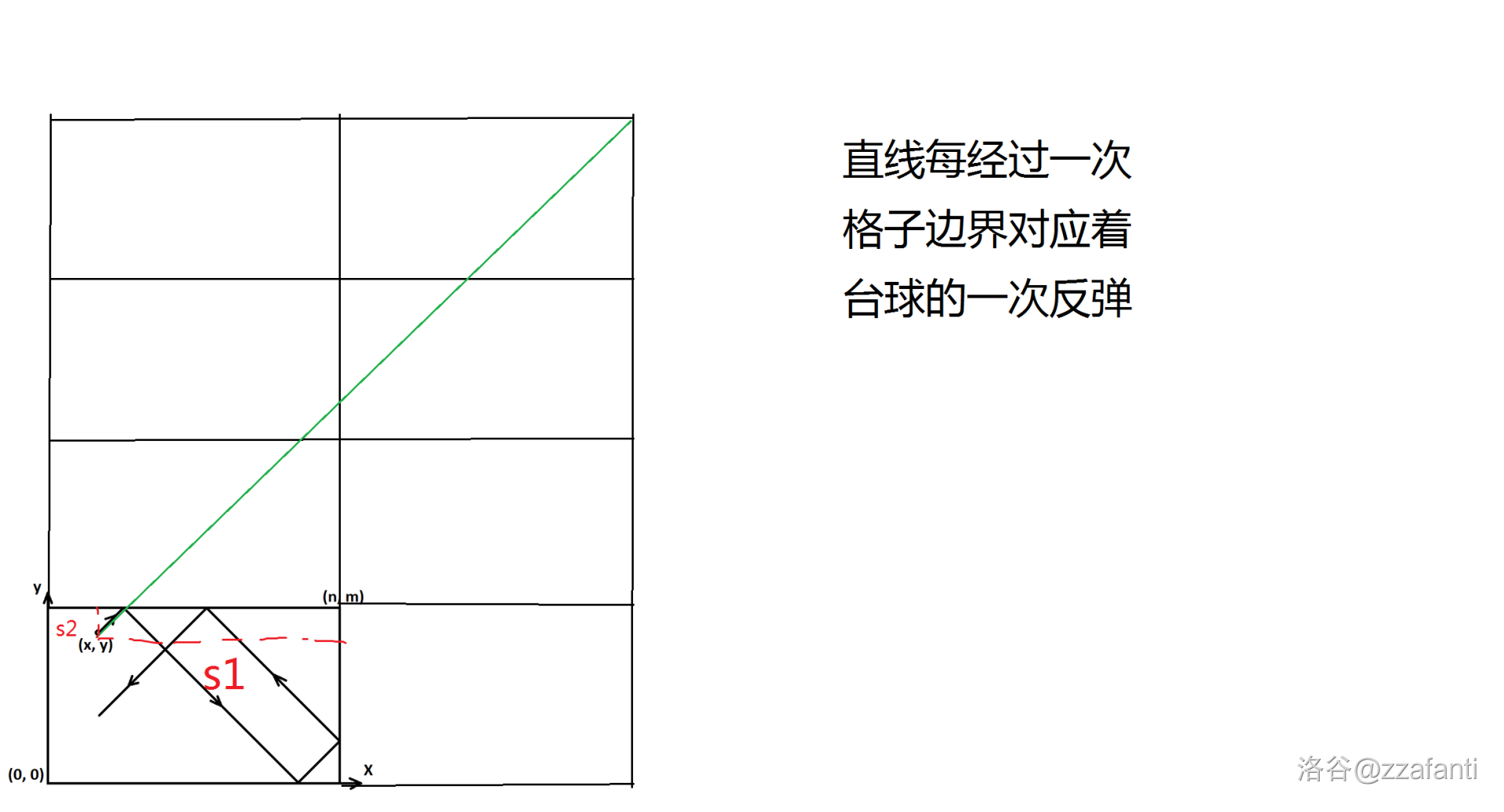
设台球初始位置横纵坐标上分别与初始方向对应的边界距离为 \(s1,s2\),设这条直线经过 \(x_0\) 次竖着的线,\(y_0\) 次横着的线(上图中 \(x_0=1,y_0=3\)),则有方程 \(s_1+nx_0=s_2+my_0\)
exgcd 求出最小的非负 \(x_0\) 与 \(y_0\) 即可。
最后落在哪个口袋需要讨论 \(x_0\) 和 \(y_0\) 的奇偶以及初速度方向。
hint
方程 \(s_1+nx_0=s_2+my_0\) 中,解出 \(x_0\) 的最小的非负整数解,带回去可以发现解出的 \(y_0\) 也一定是非负的。
code
参考代码: Submission #222446712 - Codeforces
标签:口袋,非负,nx,台球,方向,CF982E,初始 From: https://www.cnblogs.com/FreshOrange/p/17689106.html