day2 - 数组part02

力扣977. 有序数组的平方

思路1：双指针，在数组中心的两个数，作为左右指针的开始，循环比较左右指针，找出最小的平方，插入到结果数组中。

此思路是错误的，因为数组中心不见得是平方最小的数，比如数组：-4，-3，-2，-1

如果要输出的话，第一个就应该输出-1,并不是最中心的数。

思路2：那我先遍历数组，找出绝对值最小的数，左右双指针可不可以？好像可以，但是太麻烦了。

为什么？因为要先找到最小绝对值数，然后从他开始左右扩张，那么就面临问题：最小绝对值作为左指针还是右指针？如果最小绝对值在边界上，那么左右指针会面临越界。还要进行判断，虽然应该不麻烦。但是还需考虑数组只有一个数的情况等。

最佳思路3：我们之所以被边界的处所困扰，就是因为我们要制作一个从小到大的数组，因此要找到绝对值最小的数，从这个数遍历到两端。而这里的问题就在于，绝对值最小的数的位置可能在处于任何地方，但是最后左右指针一定会归于两侧。莫不如从两侧出发向中间遍历，从数组尾部开始向前插入数字。

思路：左指针指向0，右指针指向nums.size() - 1，比较两个指针指向的数字的平方的大小，将较大的数字，插入到result的尾部，并且要设置一个result下标的变量，然后这个变量--；

代码：

vector<int> sortedSquares(vector<int>& nums) {
    vector<int> result(nums.size(), 0);
    
    for (int i = 0, j = nums.size() - 1, k = nums.size() - 1; i <= j;)
    {
        if (nums[i] * nums[i] > nums[j] * nums[j])
        {
            result[k--] = nums[i] * nums[i];
            i++;
        }
        else
        {
            result[k--] = nums[j] * nums[j];
            j--;
        }
    }
    return result;
}

力扣209. 长度最小的子数组

思路：滑动窗口，左指针不动，右指针向右移动，循环遍历右指针，如果sum大于等于target了，那么就是开始移动左指针，并且更新最小数组的值。

代码实现比较难想

int minSubArrayLen(int target, vector<int>& nums) {
    //result要最小值，因此赋值一个最大值
    int result = INT32_MAX;
    //记录当前两个指针之间的和，用来判断怎样移动指针
    int sum = 0;
    //右指针移动
    for (int i = 0, j = 0; j < nums.size(); j++)
    {
        //总和加上当前右指针指向的数字
        sum += nums[j];
        //如果加完后，总和满足大于等于target的条件了，那么开始移动左指针
        while (sum >= target)
        {
            //首先计算满足这个条件的序列长度，如果是最小的就记录下来
            result = min(j - i + 1, result);
            //然后左指针向右移动一次，更新下标及总和
            sum -= nums[i];
            i++;
        }
        //左指针移动完毕，继续移动右指针
    }
    //返回结果
    return result == INT32_MAX ? 0 : result;
}

力扣59. 螺旋矩阵2

思路：这题主要就是考思路吧，考对数组的操作，重点思路就是，不算中心点的情况下，每一圈要转4下，并且每下填写到倒数第二位数，重要的是我们要转n/2圈， 因为每次转一圈，相当于上下两层，而一列有n个数，就是转n/2圈。

整体流程：外层循环n/2圈，每圈4个for循环，分别对应向右、向下、向左、向上，如图所示

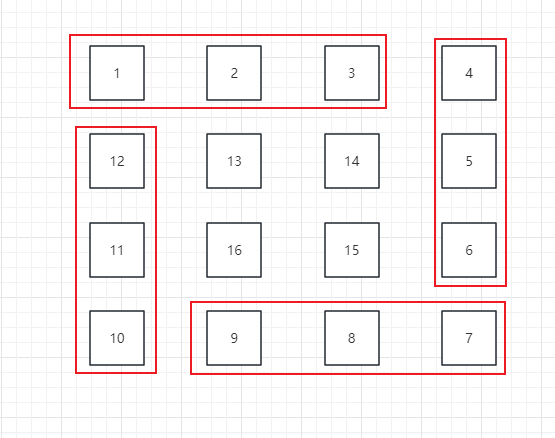
注意这一层循环的起始位置是0，0开始，0，n-1结束，四次循环后，最外层已经填充好了。

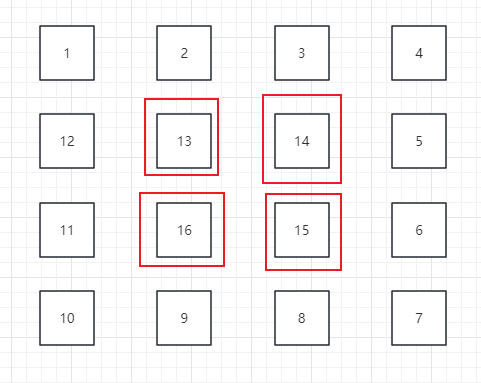
内圈的，这一层从1,1开始，到n-1-1结束。

如果再次扩大n的值，不难发现，起始位置是从0,0开始，每一圈数字填充完毕后，下一圈是从1,1开始的

因此一圈循环结束后要对起始的横纵坐标加1.

而结束位置最外圈的到n-1结束，内圈是n-1-1结束，不难发现每次循环会多减1.

代码如下

vector<vector<int>> generateMatrix(int n) {
    //返回的结果数组
    vector<vector<int>> result(n, vector<int>(n, 0));
    //一共n/2圈
    int loop = n / 2;
    //用来赋值中心的数
    int mid = n / 2;
    //起始坐标
    int start = 0;
    //每圈结束的偏移值
    int offset = 1;
    //填充数用的
    int count = 1;
    int i, j;
    //一共loop圈
    while(loop--)
    {   
        //一圈转4下，这是第一下
        //起始是start开始，把行固定不动，列动，所以列为i，行为start
        //循环结束后，i已经到达n - offset的了
        for (i = start; i < n - offset; i++)
        {
            result[start][i] = count++;
        }
        //起始列是start，行不动，因此行时i，列是j
        //循环结束，i和j的值都是n-offset
        for (j = start; j < n - offset; j++)
        {
            result[j][i] = count++;
        }
        //现在相当于填充起始位置在右下角，i，j值已经是右下角了，不需要动了。
        //然后固定i也就是行，移动列到start的位置
        for (; i > start; i--)
        {
            result[j][i] = count++;
        }
        //固定列移动回左上角起点位置
        for (; j > start; j--)
        {
            result[j][i] = count++;
        }
        //一圈结束后,start从0,0变为1,1，因此start++
        //offset会增大1
        start++;
        offset++;
    }
    //填充中间的数
    if (n % 2 == 1)
    {
        result[mid][mid] = count;
    }
    return result;
}