E An Interesting Sequence
题意:
请构造一个总和最小,长度为n且首项为k,并且相邻两项的gcd = 1的数组,输出数组各项之和。
分析:
显然对于n的奇数和偶数我们要进行分类讨论,我们希望数组的和更小,并且gcd = 1,那么我们只需要在数组中添加2和3即可。
不管什么情况,数组的第二位我们一定要找到第一个不能整除k的质数,所以我们筛完质数再找到这个值。
然后奇偶位子上都放2 3 2 3即可,特盘奇数情况是不是非要先放3即可。
void init() {
for(int i = 2 ; i < N ; i ++ ) {
if(!st[i]) primes[cnt ++ ] = i;
for(int j = 0 ; primes[j] * i < N ; j ++ ) {
st[primes[j] * i] = true;
if(i % primes[j] == 0) break;
}
}
}
signed main() {
init();
cin >> n >> k;
int t = 0;
for(int i = 0 ; i < cnt; i ++ ) {
int p = primes[i];
if(k % p) {
t = p;
break;
}
}
if(n & 1) {
cout << n / 2 * 5 - 5 + k + t + (t % 2 == 0) + 2 << endl;
}
else {
cout << n / 2 * 5 - 5 + k + t << endl;
}
}
F Infinity Tree
题意:
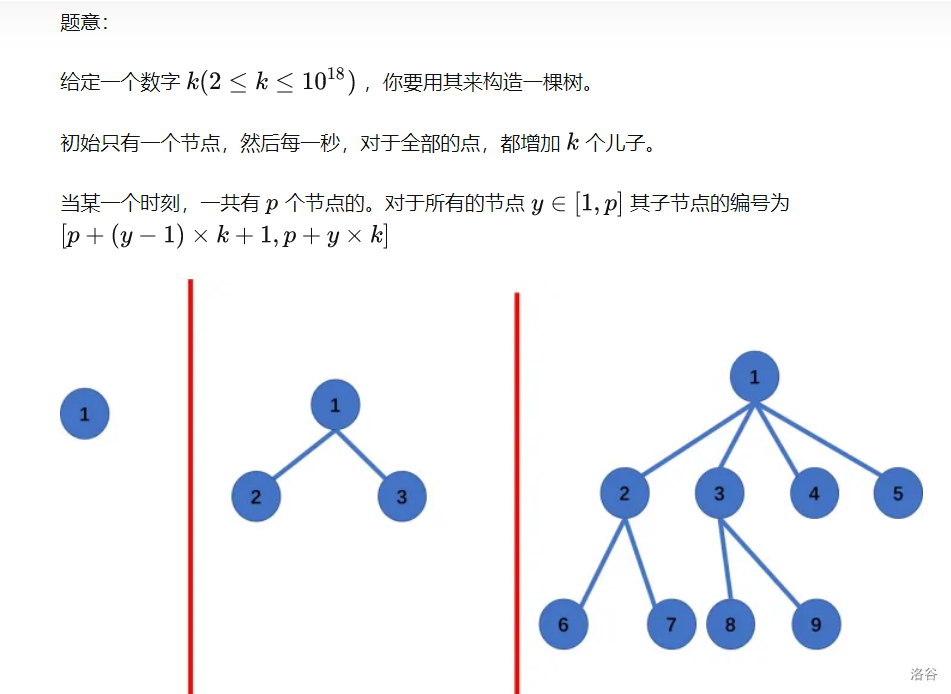
现在给出<u,v> 求出LCA(u,v)
分析:
首先我们可以知道每个时刻的节点数 i 时刻 节点就有 pow[(1+k),i-1]
可以预处理每个时间的节点个数 p[i]
接下来就是找父亲 因为深度不会很深 所以直接暴力找即可
怎么找一个点的父亲 ? 肯定是能够计算出来的
我们可以通过上一个时间节点个数p[i-1] 【即小于当前节点的最近的时间节点数】和当前节点算出父亲节点
最后<u,v>谁的节点大 就往上跳 直到节点重合
void solve() {
int k, x, y;
cin >> k >> x >> y;
__int128 xx = 1;
for(xx = 1 ; xx < x ; xx *= (k + 1));
__int128 yy = 1;
for(yy = 1 ; yy < y ; yy *= (k + 1));
xx /= (k + 1), yy /= (k + 1);
while(x != y) {
if(x > y) {
x = (x - xx + k - 1) / k;
for(xx = 1 ; xx < x ; xx *= (k + 1));
xx /= (k + 1);
}
if(x < y) {
y = (y - yy + k - 1) / k;
for(yy = 1 ; yy < y ; yy *= (k + 1));
yy /= (k + 1);
}
}
cout << x << endl;
}
J A Game about Increasing Sequences
题意:
Alice,Bob在一个数组上玩游戏。
二人轮流取走头部或者尾部的一个数,每次取的数要严格大于之前取的全部的数。
无法取到的算输。
分析:
考虑两端开始的最长连续上升序列分别为x和y
若x和y都为偶数,那么先手必输,因为不管先手取哪一端的,后手都可以取先手同一端的数字。
若x和y都为奇数,那么先手必赢,因为只要先手取较大的一端开始,之后只能取这一段的数字,先手必赢
若x和y中有一个为奇数,那么先手也必赢,因为只要先手取为奇数的那端开始,之后就是两端为偶数的必败局面,先手必赢
void solve(){
cin>>n;
F(i,1,n) cin>>a[i];
int x=1;
dF(i,n-1,1){
if(a[i]>a[i+1]) x++;
else break;
}
int y=1;
F(i,2,n){
if(a[i]>a[i-1]) y++;
else break;
}
if(x&1||y&1) cout<<"Alice\n";
else cout<<"Bob\n";
}
B Non-decreasing Array

分析

int f[N][N]; // 第i位 删除j次 但是保留i位置 的最大值
int calc(int l, int r) {
return (a[r] - a[l]) * (a[r] - a[l]);
}
signed main() {
cin >> n;
for(int i = 1; i <= n ; i ++ ) cin >> a[i];
for(int i = 1 ; i <= n ; i ++ )
for(int j = 0 ; j <= i - 2 ; j ++ )
for(int k = 0 ; k <= j ; k ++ ) {
int pos = i - k - 1; // 删除[pos + 1, i - 1]的区间:[i - k + 1, i - 1] // k是长度
f[i][j] = max(f[i][j], f[pos][j - k] + calc(pos, i));
}
for(int i = 1 ; i <= n ; i ++ ) {
if(i * 2 > n - 2) cout << f[n][n - 2] << endl;
else cout << f[n][2 * i] << endl;
}
return 0;
}
G Good Permutation
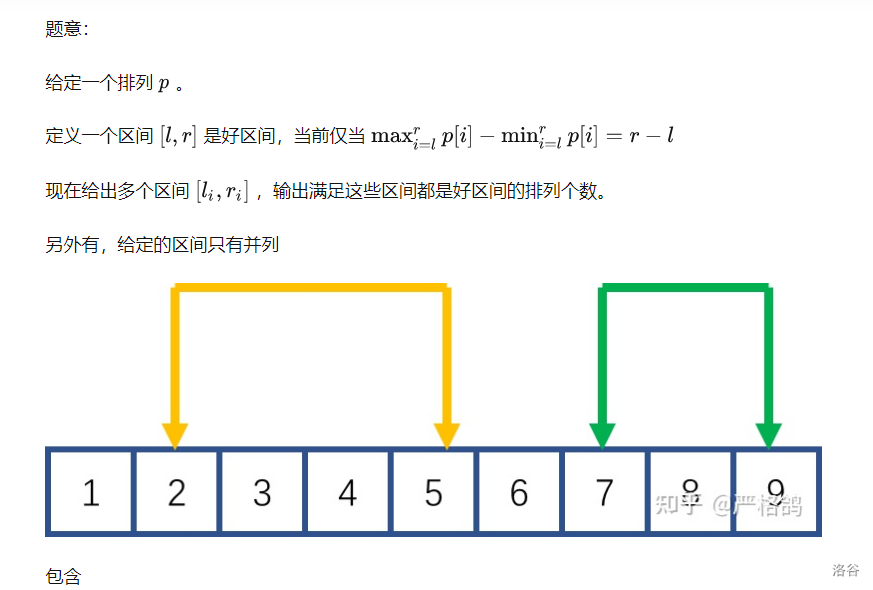
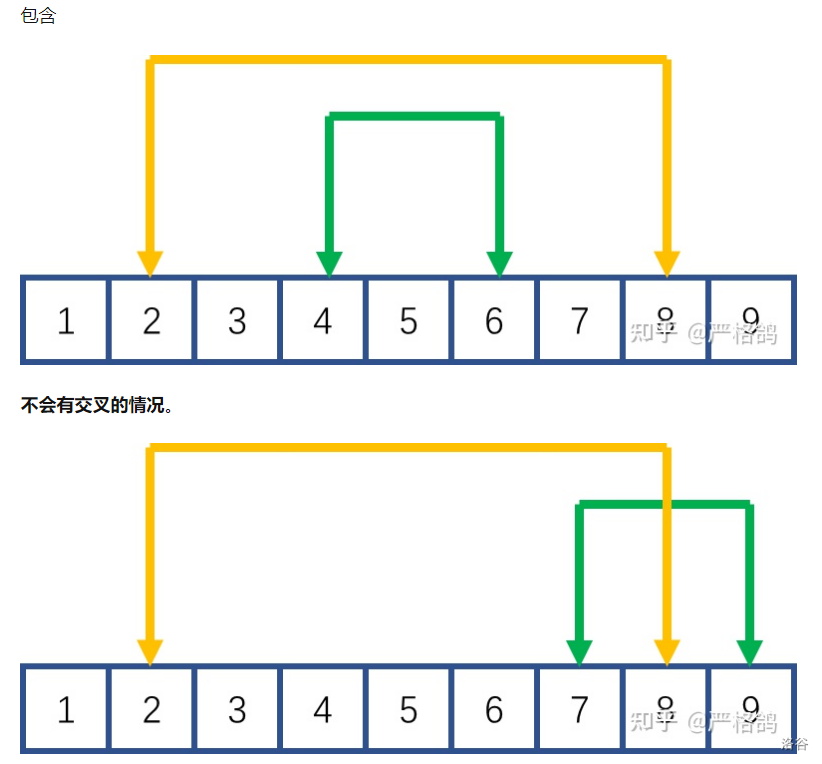


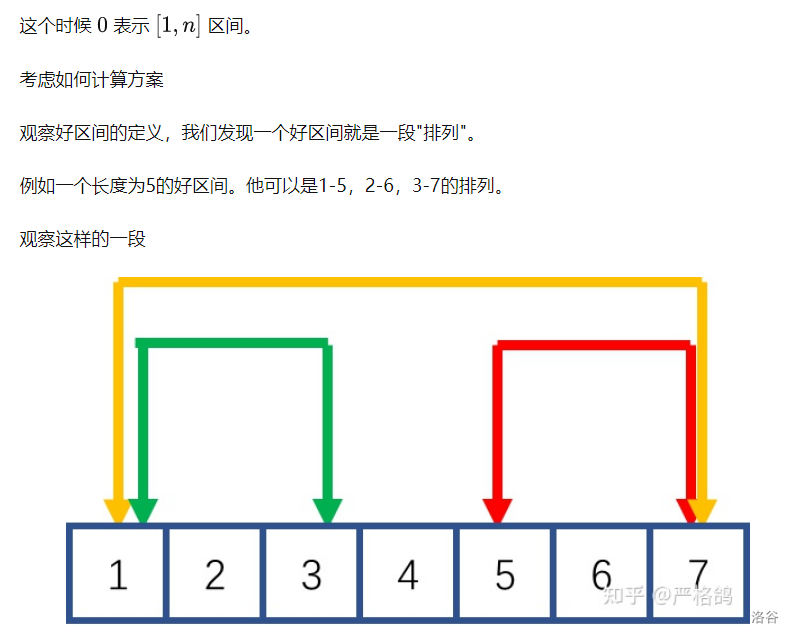

ll fac[N];
vector<int>st[N],ed[N],g[N];
int len[N];
ll dfs(int u) {
ll res = 1;
int s = 0;
for (int v : g[u]) {
res *= dfs(v);
s += len[v];
res %= mod;
}
res *= fac[len[u] - s + g[u].size()];
res %= mod;
return res;
}
void slove() {
fac[0] = 1;
for (int i = 1; i <= 1000005; i++) {
fac[i] = i * fac[i - 1] % mod;
}
cin >> n >> m;
vector<pair<int, int>>pp;
pp.push_back({ 0,0 });
for (int i = 1; i <= m; i++) {
int l, r; cin >> l >> r;
pp.push_back({ l,r });
}
sort(pp.begin(), pp.end());
for (int i = 1; i < pp.size(); i++) {
if (pp[i] != pp[i - 1]) {
int L = pp[i].first, R = pp[i].second;
len[i] = R - L + 1;
st[L].push_back(i);
ed[R].push_back(i);
}
}
for (int i = 1; i <= n; i++) {
sort(st[i].begin(), st[i].end(), [](int a, int b) {return len[a] > len[b]; });
sort(ed[i].begin(), ed[i].end(), [](int a, int b) {return len[a] < len[b]; });
}
stack<int>stk; stk.push(0);
for (int i = 1; i <= n; i++) {
for (int x : st[i]) {
stk.push(x);
}
for (int x : ed[i]) {
if (x == stk.top()) {
stk.pop();
int fa = stk.top();
g[fa].push_back(x);
}
}
}
len[0] = n;
cout << dfs(0) << endl;
}
L Quadruple
题意:
q次询问,每次询问给出l,r.计算出s[l~r]中为"icpc"的字串数量
分析
考虑用前缀和 s[i] 表示前i个中icpc的个数为多少个
但是答案 只是 s[r]-s[l-1] 肯定是不够的
还要
减去 [1,l-1]中 i 的个数×[l,r]中cpc的个数
减去[1,l-1]中ic的个数×[l,r]中pc的个数
减去[1,l-1]中icp的个数×[l,r]中c的个数
发现有很多子问题 只要一直划分就好
代码是未取模版本
int ICPC[N], ICP[N], CPC[N];
int IC[N], CP[N], PC[N];
int I[N], C[N], P[N];
int x, a, b, p;
struct Node {
int l, r;
} q[N];
int PC_sum(int l, int r) {
return PC[r] - PC[l - 1] - P[l - 1] * (C[r] - C[l - 1]);
}
int CPC_sum(int l, int r) {
return CPC[r] - CPC[l - 1]
- C[l - 1] * PC_sum(l, r)
- CP[l - 1] * (C[r] - C[l - 1]);
}
signed main()
{
cin >> n >> m;
cin >> s;
s = "?" + s;
cin >> x >> a >> b >> p;
for(int i = 1; i <= n ; i ++ )
{
// 继承
I[i] = I[i - 1], C[i] = C[i - 1], P[i] = P[i - 1];
IC[i] = IC[i - 1], CP[i] = CP[i - 1], PC[i] = PC[i - 1];
ICPC[i] = ICPC[i - 1], ICP[i] = ICP[i - 1], CPC[i] = CPC[i - 1];
if(s[i] == 'I') {
I[i] ++ ;
}
else if(s[i] == 'C') {
C[i] ++ ;
IC[i] += I[i - 1];
PC[i] += P[i - 1];
CPC[i] += CP[i - 1];
ICPC[i] += ICP[i - 1];
}
else if(s[i] == 'P') {
P[i] ++ ;
CP[i] += C[i - 1];
ICP[i] += IC[i - 1];
}
}
// 预处理询问
for(int i = 1; i <= m ; i ++ ) {
x = (a * x + b) % p;
q[i].l = x % n + 1;
}
for(int i = 1; i <= m ; i ++ ) {
x = (a * x + b) % p;
q[i].r = x % n + 1;
}
int ans = 0;
for(int i = 1; i <= m; i ++ ) {
auto [l, r] = q[i];
if(l > r) swap(l, r);
int res = ICPC[r] - ICPC[l - 1]
- I[l - 1] * CPC_sum(l, r)
- IC[l - 1] * PC_sum(l, r)
- ICP[l - 1] * (C[r] - C[l - 1]);
ans = (ans + res) % mod;
}
cout << ans << endl;
return 0;
}