\[\large{\color{#ff0000}{\text{被xjk搏杀了,wtcl}}} \]
先说以下自己的思路,\(xjk\)提出让我手玩一下样例,发现确实挺有用的
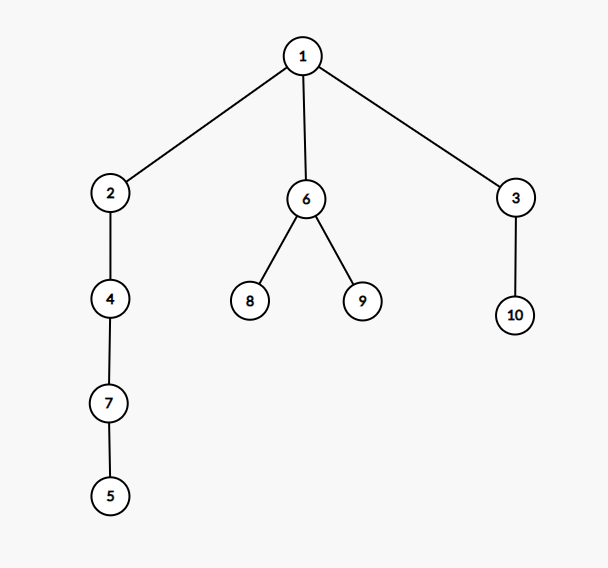
我们看这个\(2\)是怎么来的,我们发现有一种答案是选\(\{5,8\}\),我们发现不能选\(\{5,10\}\)的原因是我们无法确定\(8\)和\(9\)的区别
于是我想如果一种选点的方案不可行,当且仅当存在两个节点\(x,y\),使得这两个点到所有关键点的距离是一样的
感性理解一下,如果\(x\)移动的距离很多的话,反而是不于出现不同的距离。因此我考虑如果\(x\)从\(u\)移动到他的兄弟,会对距离产生什么样的影响
如样例,当\(x=8\)的时候,我们让他移动到\(9\),显然会让以\(8\)为根的子树内所有关键点\(+2\),让以\(9\)为根的子树内所有关键点\(-2\)
于是我们发现对于一个点\(u\)延伸出来的所有点的子树,如果有超过\(2\)个点的子树内没有关键点,那这些点内所有关键点到他们的距离是一样的,不符合题意
因此原问题就变成了考虑树上所有点连向的点中最多只有一个点的子树内没有关键点,最少可以放多少关键点
然后这个问题就做不下去了233
\(xjk\)的思路是这样:
首先,绝对显然的是这些关键节点在叶子上,否则一定不优
我们发现,如果选择两个节点\((x,y)\),则我们可以确定\(x \rightarrow y\)的这条路径上的所有点 和 这些点向外延伸出来的链
因为我们考虑如果\(d_x+d_y \leq dist(x,y)\),则我们显然可以唯一确定这个点
否则,我们可以找到一个最大的\(d\),满足\(d_x - d + d_y - d \leq dist(x,y)\),这样我们可以通过\(d_x - d\)和\(d_y - d\)唯一确定这个点和路径的交点,再通过\(d\)确定他在这条链上的深度
例如样例,我们如选择了\(5,10\),则我们可以确定的点为\(\{5,7,4,2,1,3,10,6\}\),但\(\{8,9\}\)显然不能被确定,因为我们无法通过延伸点的编号和深度来唯一确定这两个点
我们发现链不好考虑,而且是没有必要的,因此我们先把所有的链缩成一条边,最后得到的图中每个点要么度数\(> 2\),要么是叶子节点
容易想到这么建了一棵新树后对于每个点的所有儿子,必然最多只有一个儿子内没有关键点;于是我们贪心的选择,让每一个儿子就只有\(l_i-1\)个关键点
于是我们有以下计算方案:对于每一个点,记新图中与它直接相连的叶子个数为\(l_i\),则这个点对答案的贡献为\(\max{(l_i-1,0)}\)
这个做法正确的原因是对于每个节点,与它相连的非叶子节点一定已经在枚举它时都被考虑过,因此我们只用考虑对于\(l_i\)个叶子节点选\(l_i-1\)个即可
如果我们用\(set\)维护树,并直接构造新树,则做法是\(O(n\log{n})\)的,并不非常优秀,参见题解。他的代码第\(41,42\)行写的很奇怪,是可以直接写成:
for(int i=1;i<=n;i++){
d[i]-=(int)E[i].size();
//如果在新树上度为 1,那就是其中一条上出边,与一条连到附属点的边虚化
//否则减新树上所有出边
if(!vis[i])ans+=max(d[i]-1,0);//还有剩下的附属点
}
的,阅读的时候要注意一下。
我们考虑一下怎么优化
我们发现其实我们并不需要直接把新树建出来,因为我们发现对于原树的每个叶子,把他沿着一条链暴力上传,直到上传到\(deg_u \geq 3\)的点后,把贡献加到点\(u\)上即可,复杂度显然是便利整棵树
个人实现的时候是在树上找了一个\(deg_u \geq 3\)的点作为\(dfs\)时的根,在\(dfs\)中维护每个点的父亲;因为\(deg_{root} \geq 3\),因此叶子节点不会超过这个节点再跑下去。而如果找不到一个\(deg_u \geq 3\)的点,显然就是一条链,直接输出\(1\)即可
最终复杂度\(O(n)\)
标签:geq,子树内,Hard,Tree,我们,叶子,Version,节点,关键点 From: https://www.cnblogs.com/fox-konata/p/17679233.html