给定 \(k\) 个字符串 \(t\),一个字符串集合 \(S\) 与 \(n\) 次操作,初始时 \(S\) 为空。操作有三个类型:
- 将指定编号的字符串加入 \(S\) 中;
- 将指定编号的字符串从 \(S\) 中删除;
- 给定字符串 \(s\),询问 \(S\) 中所有字符串在 \(s\) 中的匹配次数之和。
\(n, k \le 10^5\),\(\sum \left|t\right| \le 10^6\),\(\sum \left|s\right| \le 10^6\)。
首先看到多模式匹配那肯定是优先想到 AC 自动机的。我们先考虑如果问题是给定一个字符串集合 \(S\) 与一个字符串 \(s\),问 \(S\) 中所有字符串在 \(s\) 中的匹配次数之和该怎么做。
很简单对吧,我们对字典树上的每一个节点都赋一个 \(val\) 值,表示匹配到当前节点的匹配次数之和。初始化终止节点的 \(val\) 为 \(1\),其他的为 \(0\),然后我们容易发现 \(val_i = val_i + val_{nxt_i}\),其中 \(nxt\) 表示失配指针,然后询问就很简单了,直接遍历整个 \(s\) 并同时维护当前走到了哪个节点,然后累加所经过的 \(val\) 即可。
再考虑 AC 自动机中加入或删除字符串的本质:
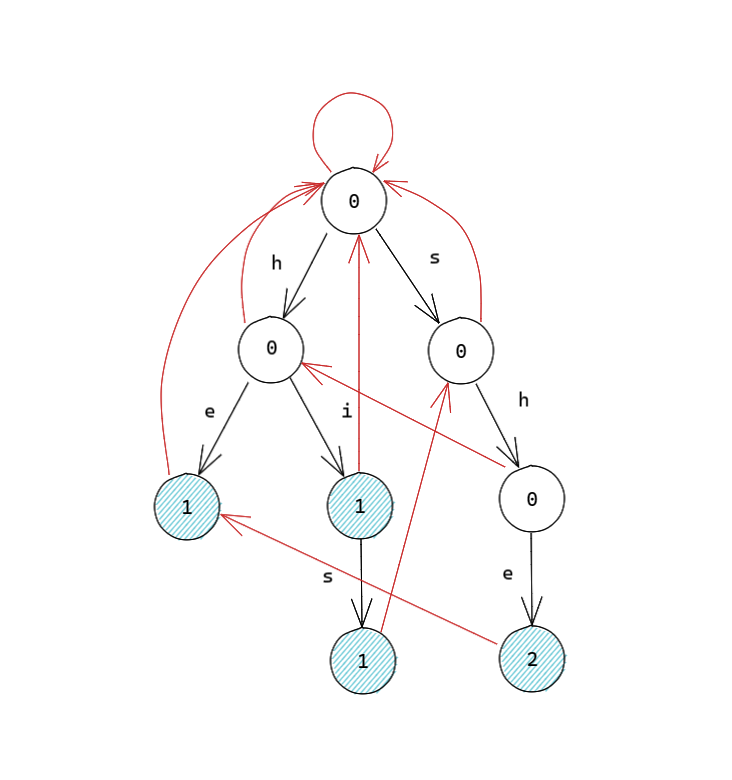
上图是由 \(\texttt{he}\)、\(\texttt{hi}\)、\(\texttt{his}\) 与 \(\texttt{she}\) 构建出的 AC 自动机,其中蓝色节点表示终止节点,红色边表示失配指针,节点中的数字代表 \(val\) 值。
我们考虑删去 \(\texttt{he}\) 这个字符串:
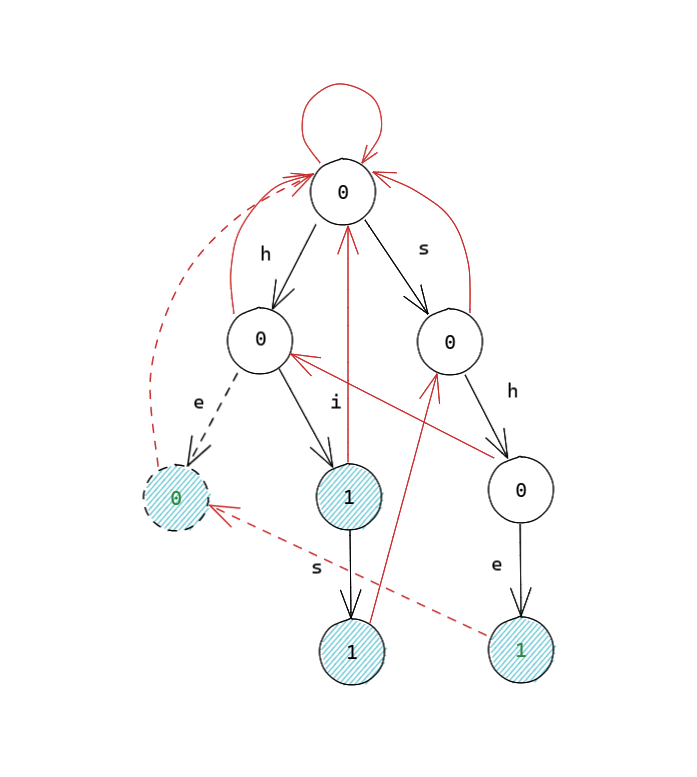
虚线代表被删除的部分,绿色代表 \(val\) 发生了变化的节点。
没看出来吗?再来一个!我们考虑删去 \(\texttt{hi}\) 这个字符串:
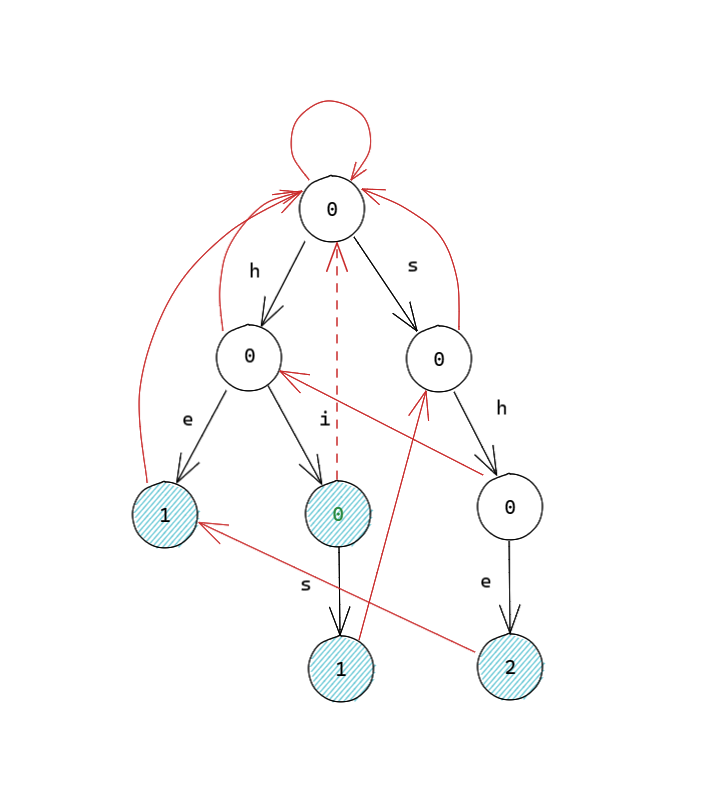
我们发现,当删除一个字符串时,不仅会影响到当前字符串终止节点的 \(val\) 会减少 \(1\),失配指针连向当前字符串终止节点的所有节点的 \(val\) 也会减少。加入字符串是同理的。
那么我们此时就有一个 \(\mathcal{O}\left(n\sum\left|t\right| + \sum \left|s\right|\right)\) 的做法了。在每次加入或删除字符串时就暴力的找出所有需要修改的节点,询问就直接按上边的方法询问就可以了。
但这显然是不够的,我们需要更优的做法。我们考虑去掉字典树上的边,来观察一下失配指针:
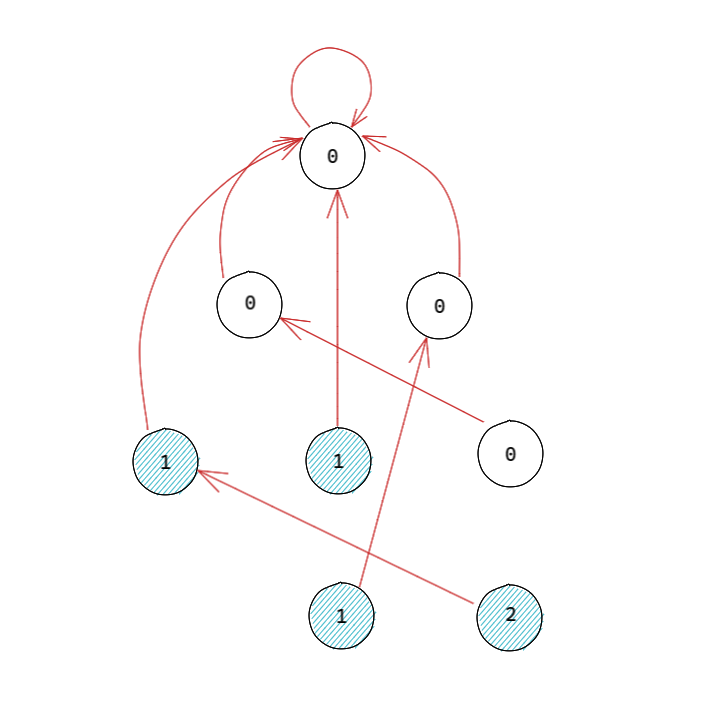
可以发现,除去初始节点的失配指针由自身转移到自身之外,失配指针天然构成一个树形结构。我们还可以看出,每次字符串修改所影响的节点全部都位于当前字符串终止节点的子树中!
那么现在就好做了。看到子树修改,我们自然会联想到将树用 DFS 序拍平然后转化为序列修改再用线段树等结构维护。但是本题是区间修改单点查询,可以转化为差分序列然后用树状数组来做(而且线段树被卡空间了),那么这样就可以做到时间复杂度 \(\mathcal{O}\left(n\log\sum\left|t\right| + \sum \left|s\right|\right)\)。
标签:right,val,Government,sum,字符串,CF163E,节点,left From: https://www.cnblogs.com/forgot-dream/p/17674583.html