图的存储
图的存储:B3643
AC Code:
#include <iostream>
#include <vector>
#include<algorithm>
using namespace std;
#define ll long long
const int maxn=1005;
// 邻接矩阵
ll a[maxn][maxn];
// 邻接表
vector<ll> adj_list[maxn];
ll n,m;
int main(){
cin>>n>>m;
// 读取边的信息并构建邻接矩阵和邻接表
for(ll i=1;i<=m;i++){
ll u,v;
cin>>u>>v;
a[u][v]=1;
a[v][u]=1; // 无向图,所以两个方向都要标记为1
adj_list[u].push_back(v);
adj_list[v].push_back(u);
}
// 输出邻接矩阵
for(ll i=1;i<=n;i++){
for(ll j=1;j<=n;j++){
cout<<a[i][j]<<" ";
}
cout<<endl;
}
// 输出邻接表
for(ll i=1;i<=n;i++){
sort(adj_list[i].begin(),adj_list[i].end());
cout<<adj_list[i].size()<< " ";
for(ll j=0;j<adj_list[i].size();j++){
cout<<adj_list[i][j]<<" ";
}
cout<<endl;
}
return 0;
}
链式前向星存图
Code:
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
#define ll long long
const int maxn=1e5+5;
struct edge{
int to;//边的目标节点
int w;//边的权重
int next;//下一条边
};
vector<edge> edges;//存储所有边
int head[maxn];//存储每个节点的第一条边
int edge_num;//边的数量
void addedge(int u,int v,int w){
edges.push_back({u,head[u],w});
//有向图
//将一条从u到v的边1添加到图中,将head[u]中原本存储的边的索引作为新边的next
head[u]=edge_num++;
//将新边的索引存储到head[u]中
}
int n,m,u,v,w;
int main(){
cin>>n>>m;
memset(head,-1,sizeof(head));//初始化,每个节点暂时没有边
for(int i=1;i<n;i++){
cin>>u>>v>>w;
addedge(u,v,w);
}
return 0;
}
图的遍历
dfs遍历
P3916 图的遍历
正向存:
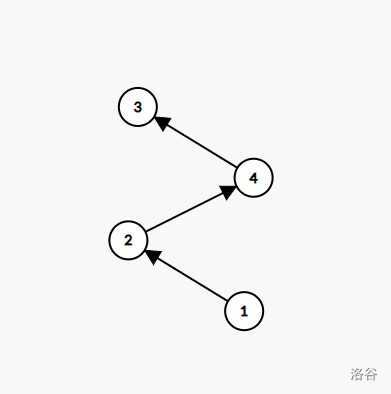
由于数据范围过大,为了节约时间反向存图
反向存:
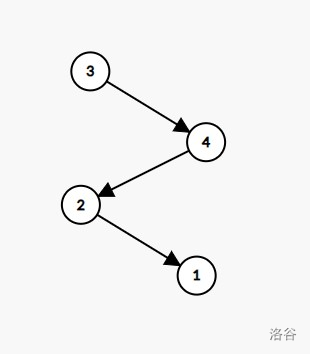
AC Code:
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int maxn=1e5+5;
int n,m,u,v;
struct node{
int to;
int next;
};
vector<node> edge;
int head[maxn];
int edgenum;
void add(int u,int v){
edge.push_back({v,head[u]});
head[u]=edgenum++;
}
int ans[maxn];
void dfs(int x,int maxx){
if(ans[x]!=0)return ;
ans[x]=maxx;
for(int i=head[x];i!=-1;i=edge[i].next){
int v1=edge[i].to;
dfs(v1,maxx);
}
}
int main(){
cin>>n>>m;
memset(head,-1,sizeof(head));
for(int i=1;i<=m;i++){
cin>>u>>v;
add(v,u);
}
for(int i=n;i>=1;i--){
dfs(i,i);
}
for(int i=1;i<=n;i++){
cout<<ans[i]<<" ";
}
return 0;
}
P2853
AC Code(dfs):
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int maxn=10005;
int k,n,m,u,v;
struct node{
int to;
int next;
};
vector<node> edge;
int head[maxn];
int edgenum;
/*
必须设为0而不是1
C++中数组和vector的下标都是从0开始
如果这里设为1,那么head[u]实际上存储的是第二条边
*/
int ans;
int a[maxn];
void add(int u,int v){
edge.push_back({v,head[u]});
head[u]=edgenum++;
}
int can[maxn];
bool vis[maxn];
void dfs(int x){
vis[x]=1;
//防止重复搜索从而爆栈,MLE
can[x]++;
for(int i=head[x];i!=-1;i=edge[i].next){
int x1=edge[i].to;
if(vis[x1]==0)dfs(x1);
}
}
int main(){
cin>>k>>n>>m;
memset(head,-1,sizeof(head));
for(int i=1;i<=k;i++){
cin>>a[i];
}
for(int i=1;i<=m;i++){
cin>>u>>v;
add(u,v);
}
for(int i=1;i<=k;i++){
dfs(a[i]);
memset(vis,0,sizeof(vis));
//切换牧场时初始化标记数组
}
for(int i=1;i<=n;i++){
if(can[i]==k)ans++;
}
cout<<ans;
return 0;
}
bfs遍历
P2853
AC Code(bfs):
#include<iostream>
#include<vector>
#include<cstring>
#include<queue>
using namespace std;
const int maxn=10005;
int k,n,m,u,v;
struct node{
int to;
int next;
};
vector<node> edge;
int head[maxn];
int edgenum;
/*
必须设为0而不是1
C++中数组和vector的下标都是从0开始
如果这里设为1,那么head[u]实际上存储的是第二条边
*/
int ans;
int a[maxn];
void add(int u,int v){
edge.push_back({v,head[u]});
head[u]=edgenum++;
}
int can[maxn];
bool vis[maxn];
void bfs(int x){
queue<int> q;
vis[x]=1;
q.push(x);
while(!q.empty()){
int cur=q.front();
q.pop();
can[cur]++;
for(int i=head[cur];i!=-1;i=edge[i].next){
int x1=edge[i].to;
if(vis[x1]==0){
vis[x1]=1;
q.push(x1);
}
}
}
}
int main(){
cin>>k>>n>>m;
memset(head,-1,sizeof(head));
for(int i=1;i<=k;i++){
cin>>a[i];
}
for(int i=1;i<=m;i++){
cin>>u>>v;
add(u,v);
}
for(int i=1;i<=k;i++){
bfs(a[i]);
memset(vis,0,sizeof(vis));
}
for(int i=1;i<=n;i++){
if(can[i]==k)ans++;
}
cout<<ans;
return 0;
}
综合
P5318
排序过程:把
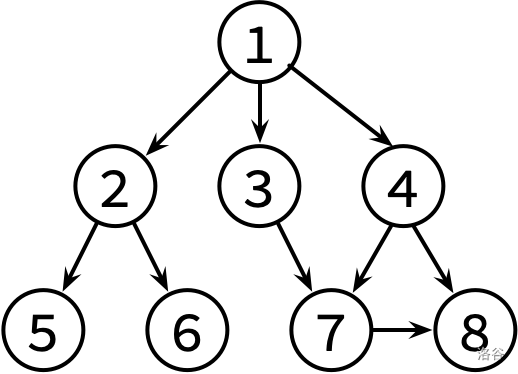
排序成

这个样子就可以了
也就是只排序同一层的文献
AC Code:
#include<iostream>
#include<vector>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn=1e6+5;
int n,m,x,y;
struct node{
int to;
int next;
};
vector<node> edge1;
vector<node> edge;
int head[maxn];
int edge_num;
bool cmp(node x,node y){//注意判定条件!!!
if(x.to==y.to)return x.next>y.next;
return x.to<y.to;
}//从大到小录入,只需排序同一层文献,文献层次保持不变!
void add(int u,int v){
edge.push_back({v,head[u]});
head[u]=edge_num++;
}
int vis_dfs[maxn];
void dfs(int x){
vis_dfs[x]=1;
for(int i=head[x];i!=-1;i=edge[i].next){
int x1=edge[i].to;
if(vis_dfs[x1]==0){
cout<<x1<<" ";
dfs(x1);
}
}
}
int vis_bfs[maxn];
void bfs(int x){
vis_bfs[x]=1;
queue<int> q;
q.push(x);
while(!q.empty()){
int cur=q.front();
q.pop();
for(int i=head[cur];i!=-1;i=edge[i].next){
int cur1=edge[i].to;
if(vis_bfs[cur1]==0){
cout<<cur1<<" ";
vis_bfs[cur1]=1;
q.push(cur1);
}
}
}
}
int main(){
cin>>n>>m;
memset(head,-1,sizeof(head));
for(int i=1;i<=m;i++){
cin>>x>>y;
edge1.push_back({x,y});
add(x,y);
}
sort(edge1.begin(),edge1.end(),cmp);
for(int i=1;i<=m;i++){
add(edge1[i].to,edge1[i].next);
}
cout<<"1 ";
dfs(1);
cout<<endl<<"1 ";
bfs(1);
return 0;
}
图的连通性
前置知识:时间戳和追溯点
时间戳:dfn[u]表示节点u深度优先遍历的序号。
追溯点:low[u]表示节点u或u的子孙能通过非父子边追溯到的dfn最小值,即回到最早的过去。
Tarjan算法
用于求解桥和割点
桥判定法则:无向边x-y是桥,当且仅当存在x的一个子节点y时,满足low[y]>dfn[x]。
也就是说,若孩子的low值比自己的dfn值大,说明孩子回不到起点,则从该节点到这个孩子的边为桥。
Code:
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int maxn=1e5+5;
int n,m,u,v,root;//root为根节点
struct node{
int to;
int next;
};
vector<node> edge;
int head[maxn];
int edgenum;
void add(int u,int v){
edge.push_back({v,head[u]});
head[u]=edgenum++;
}
int dfn[maxn],low[maxn],nodenum=1;//时间戳,追溯点,节点序号
void tarjan_bridge(int u,int fa){//求桥
//从u出发,fa为u的父节点
dfn[u]=low[u]=nodenum++;
for(int i=head[u];i!=-1;i=edge[i].next){
int v=edge[i].to;
if(v==fa){//如果v是u的父节点
continue;
}
if(dfn[v]==0){//如果v点未赋值
tarjan_bridge(v,u);//访问v,u为v的父节点
low[u]=min(low[u],low[v]);
if(low[v]>dfn[u]){//判断是否符合条件
cout<<u<<"-"<<v<<"是桥"<<endl;
}
}else{//如果赋了值,那么更新low并返回
low[u]=min(low[u],dfn[v]);
}
}
}
int main(){
while(cin>>n>>m){
memset(head,-1,sizeof(head));
while(m--){
cin>>u>>v;
add(u,v);
add(v,u);
}
for(int i=1;i<=n;i++){//可能有多个桥,依次访问每个节点
if(dfn[i]==0){//如果没访问过
tarjan_bridge(i,0);
}
}
}
return 0;
}
割点判定法则:
若x不是根节点,则x是割点,当且仅当存在x的一个子节点y,满足low[y]>=dfn[x];
若x是根节点,则x是割点,当且仅当至少存在两个子节点,满足该条件。
也就是说,如果不是根,且孩子的low值大于或等于自己的dfn值,则该节点就是割点;
如果是根,则至少需要两个孩子满足条件。
Code:
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int maxn=1e5+5;
int n,m,u,v,root;//root为根节点
struct node{
int to;
int next;
};
vector<node> edge;
int head[maxn];
int edgenum;
void add(int u,int v){
edge.push_back({v,head[u]});
head[u]=edgenum++;
}
int dfn[maxn],low[maxn],nodenum=1;//时间戳,追溯点,节点序号
void tarjan_cut(int u,int fa){//求割点
//从u出发,fa为u的父节点
dfn[u]=low[u]=nodenum++;
int count=0;//记录有几个儿子满足条件
for(int i=head[u];i!=-1;i=edge[i].next){
int v=edge[i].to;
if(v==fa){//如果v是u的父节点
continue;
}
if(dfn[v]==0){//如果v点未赋值
tarjan_cut(v,u);//访问v,u为v的父节点
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){//判断是否符合条件
count++;//满足条件的儿子+1
if(u!=root||count>=2){
//如果u不是树根 或者 是树根且有两个以上儿子满足要求
cout<<u<<"是割点"<<"\n";//u是割点
}
}
}else{//如果赋了值,那么更新low并返回
low[u]=min(low[u],dfn[v]);
}
}
}
int main(){
while(cin>>n>>m){
memset(head,-1,sizeof(head));
while(m--){
cin>>u>>v;
add(u,v);
add(v,u);
//无向图
}
for(int i=1;i<=n;i++){
//有可能是非连通图,需要从每个节点开始检查
if(dfn[i]==0){//如果没访问过
root=i;//记录起点作为树根
tarjan_cut(i,0);
}
}
}
return 0;
}