从洛谷搬过来并做了些许润色,后面或许还会增加内容(?
第一次学的时候似乎忘记写博客了捏
网络流全称网络流理论,是把量类比水流的一种模型。
最大流
基本芝士
对于最大流问题,有一种经典的不能在经典的情景:有一个能生产无限水的自来水厂,若干能承载无线水的节点和家三中节点,点与点之间有若干条流量有限制的单向水管,询问每时刻到家的水流量最大是多少。
而在网络流中,则会使用若干专有名词来替换该情景,其概念如下:
- \(\color{#90EE90}{流量}\),即水流量,常用\(f\)表示。
- \(\color{#90EE90}{容量}\),即水管的水流量限制,常用\(c\)表示。
- \(\color{#90EE90}{残量}\),即容量-流量,常用\(r\)表示。
- \(\color{#90EE90}{源点}\),即自来水厂,常用\(S\)表示。
- \(\color{#90EE90}{汇点}\),即家,常用\(T\)表示。
知道了这些以后,我们就可以用形式化的语言来阐述网络流问题:
- \(\color{#90EE90}{反对称性}\space f[u \rightarrow v] = -f[v \rightarrow u]\)。
- \(\color{#90EE90}{内部流量守恒}\) 对于\(u \neq S,T\),流入量与流出量相等。
- \(\color{#90EE90}{外部流量守恒} \space \sum\limits_x f[S \rightarrow x] = \sum\limits_y f[y \rightarrow T]\)。
- \(\color{#90EE90}{容量限制}\space f[u \rightarrow v] \leq c[u \rightarrow v]\)。
计算出满足以上四个性质,且能使得\(\sum\limits_x f[x \rightarrow T]\)最大的\(f\),便是最大流问题。
问题已经很清晰了,那么如何解决呢?要解决一个大规模问题,拆分是一个重要手段。而在拆分之前,我们需要一个定理为我们的正确性提供支撑,那就是\(\color{Skyblue}{残量调整定理}\):
对于网络\(c\),记所有可能的合法流的集合为\(F_c\)。对于任意一个\(f \in F_c\),记残量网络\(r = c - f\),则有\(F_c = f + F_r\)。用文字语言来描述就是一个网络上的所有可能的合法流可以经由残量网络调整而来。
【证明口胡】 对于边\(u \rightarrow v\)有\(f[u \rightarrow v] = w\),根据反对称性有\(f[u \rightarrow v] = -w\),则残量\(r[v \rightarrow u] = c[v \rightarrow u] + w\)。我们之后调整时可以把残量上多出来的部分给撤回去,即为每条边创造一条容量为\(0\)的反向边,每次正向边流量增加,反向边就增加对应的值,之后经过反向边时也同理。正向边加大流量便是加大流量,反向边增大流量相当于把正向边的流量撤回,这样便可以进行增流与撤回的操作。把所有的流都撤回去,就又变成了原网络,因此\(F_c \leq f + F_r\),随后又因网络结构不变\(F_c \geq f + F_r\),两者合并就是\(F_c = f + F_r\)。(了解即可,反正也不考证明)
有了这条定理,我们要做的操作也就呼之欲出:
\(\color{#90EE90}{增广路}\),即残量网络\(r\)中,满足每条边的\(r\)都大于\(0\)的一条从\(S\)到\(T\)的路径。
\(\color{#90EE90}{增广}\),即把增广路上每条边流该增广路上最小的\(r\)的操作。
对于增广路也有\(\color{Skyblue}{增广路定理}\),即当一个残量网络中不存在增广路,那么此时就是该网络的最大流(证明不想打了,详见神の博客)
算法
考虑直接暴力dfs,那么喜提TLE,来看看下面这张经典的图:

不好意思放错了,是下面这张:
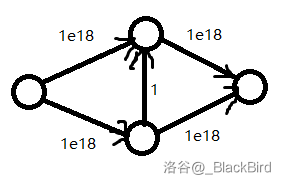
有没有一种never gonna give you up被骗了的感觉,dfs这种好骗的搜索是酱紫的……
这种算法被称为\(\color{Pink}{Ford-Fulkerson(FF)算法}\),这样的时间复杂度是\(O(m * 最大流量)\),即找增广路所需的O(m)乘上找的次数,造数据的大手一挥,增广路长度为\(1\),那就要找最大流量次,找抽一般的复杂度。
那么有没有办法优化一下呢?显然是有的,就是用bfs找。
为什么dfs不彳亍而bfs就彳亍呢?我们从bfs的性质分析:
显然每次bfs找到的增广路一定是当前残量网络最短的一条增广路。观察之前的图可以发现dfs败在了中间的那条边与它的反向边上。dfs一直在正向边与反 向边反复横跳,最后就寄了。而bfs要利用反向边,必须走到一条边的尽头再往回走,而每次走最短的bfs显然是不会碰的。
这种算法被称为\(\color{Pink}{Edmonds–Karp(EK)算法}\),在时间复杂度上是\(O(nm^2)\),即增广路长度\(1 \sim n\)的\(O(n)\),增广路找一次\(O(m)\),共\(m\)条。
看起来EK已经能用了,但它还是远不及我们下面的这位常用(用力地敲击黑板!):
\[\huge D \space I \space N \space I \space C \]\(\color{Pink}{Dinic算法}\)是对\(EK\)算法的进一部优化,先bfs分层再dfs多路增广,知道再也找不到增广路。
酱紫有什么好处呢?好处就是每一轮一定可以让增广路长度变大,这样时间复杂度就是\(O(n^2m)\),共分\(n\)层,增广路不超过\(m\)条,增广路长度\(1 \sim n\),把\(EK\)的一只\(m\)变成了一只\(n\),在稠密图上显然是大大优于\(EK\)。
那么是激动人心的上代码时间:
code(古早代码,年久失调,如被卡常,不关我事)
应用
最大流
最大流当然能解决最大流问题啦
当然这里主要是讲一些问题如何转化成最大流的形式。