torch.sum()用法-截至2023年8月28日

torch.sum()维度0，1，2。比如现在有\(3\times\ 2\times3\)的张量，理解为3个\(2\times3\)的矩阵。当dim=0，1，2时分别在哪个维度上相加^[1]？下面是具体的矩阵

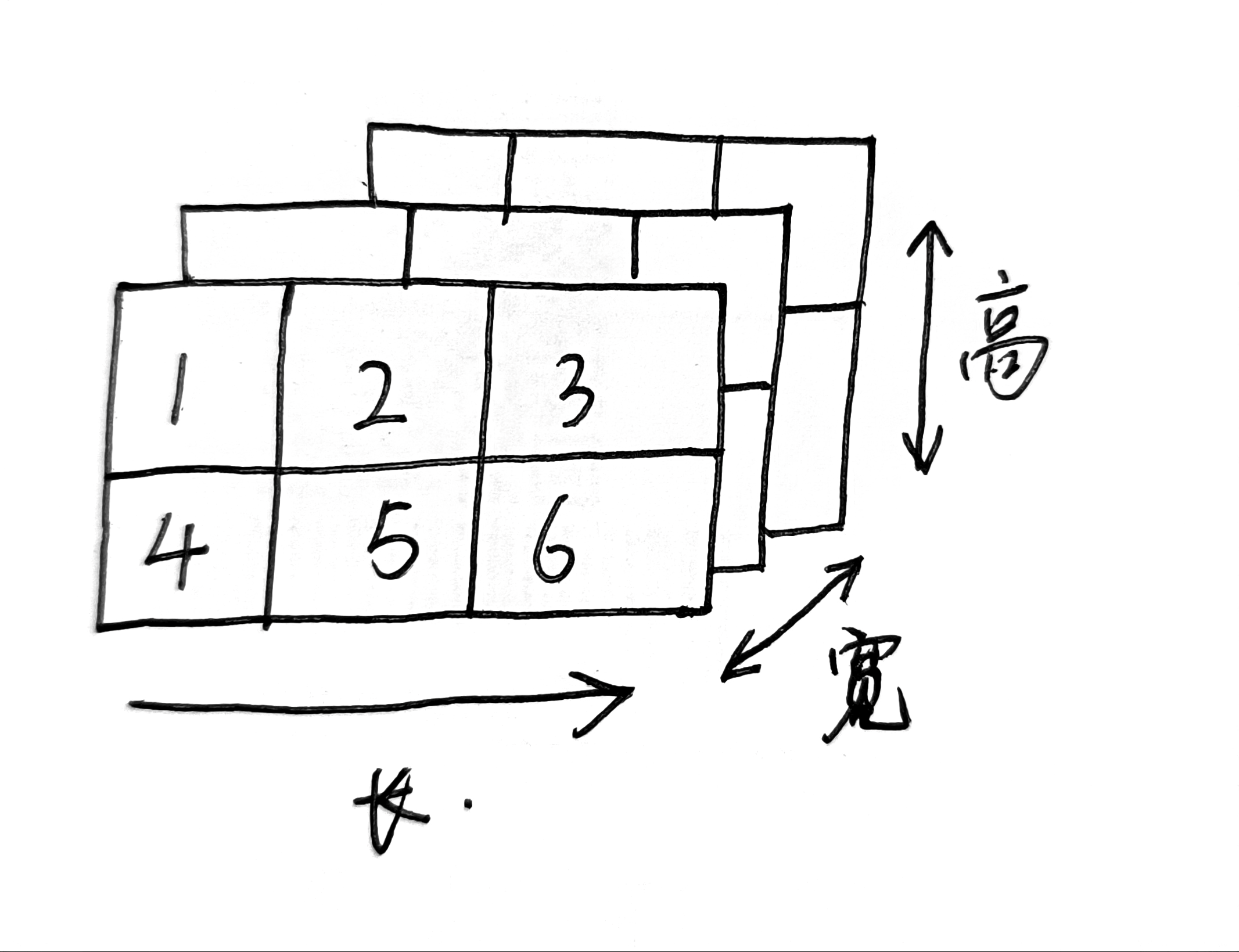
在哪个维度相加，那个维度就去掉。\(3\times2\times3\)分别就对应0，1，2三个维度。

• dim=0，最后计算结果就是\(2\times3\)。（可视化后按照宽维度相加对应元素）
• dim=1，最后计算结果就是\(3\times3\)。（可视化后按照高维度相加对应元素）
• dim=2，最后计算结果就是\(3\times2\)。（可视化后按照长维度相加对应元素）

宽和高维度是正面看的，所以不用动。而长维度是横着看，所以最后元素需要向左旋转。（具体计算时理解的，我这么表述可能不清楚）

示例代码

import torch
c = torch.tensor([[[1,2,3],
                   [4,5,6]],
                  
                  [[1,2,3],
                   [4,5,6]],
                  
                  [[1,2,3],
                   [4,5,6]]])
print(f" c size = {c.size()}")

c1=torch.sum(c , dim=0)
print(f" c1 = {c1}\n c1 size = {c1.size()}")


c2=torch.sum(c , dim=1)
print(f" c2 = {c2}\n c2 size = {c2.size()}")


c3=torch.sum(c , dim=2)
print(f" c3 = {c3}\n c3 size = {c3.size()}")

运行结果如下