后缀数组典题
约定:\(sa_i\) 表示将所有后缀排序后第 \(i\) 小的后缀的编号,\(rk_i\) 表示后缀 \(i\) 的排名,\(hgt_i=lcp(sa[i],sa[i-1])\)
[NOI2016] 优秀的拆分
求一个字符串的子串能被拆成 \(AABB\) 形式的方案数,其中 \(A,B\) 均为字符串(\(|S|\leq 300000\))。
- \(O(n^2)\)
枚举 AA 和 BB 中间的位置,用哈希即可解决,有 95 分的高分。
- \(O(nlogn)\)
考虑 \(pre_i\) 表示以 i 结尾的能被表示成 AA 形式的子串数量,\(suf_i\) 则表示以 i 开头的。那么有:
\[ans=\sum_{i=1}^{n-1}pre_isum_{i+1} \]考虑统计 \(pre\)(\(suf\) 同理)。
枚举 A 的长度 \(w\),将序列分块,其中 \(x\ mod\ w==0\) 的 x 是关键点。那么任意一组 AA 必定跨越且仅跨越两个唯一的关键点。那么就可以在相邻两个关键点出统计出所有方案。
枚举相邻两个断点 l 和 r,求出它们的前缀最长公共后缀长度 lcs 和后缀最长公共前缀长度 lcp 之和 len:
表示经过两个断点且开头距离 w 的最长公共子串。
lcp 和 lcs 使用 sa 求出。
如果 \(len<w\) ,说明没有同时经过这两个断点的 AA 串。
\(f_{r+lcp−(lcp+lcs−1)→r+lcp−1}+1\)。这个区间修改可以方便的用差分解决。
如下图,即两条紫线以及之间的子串为 AA 串:
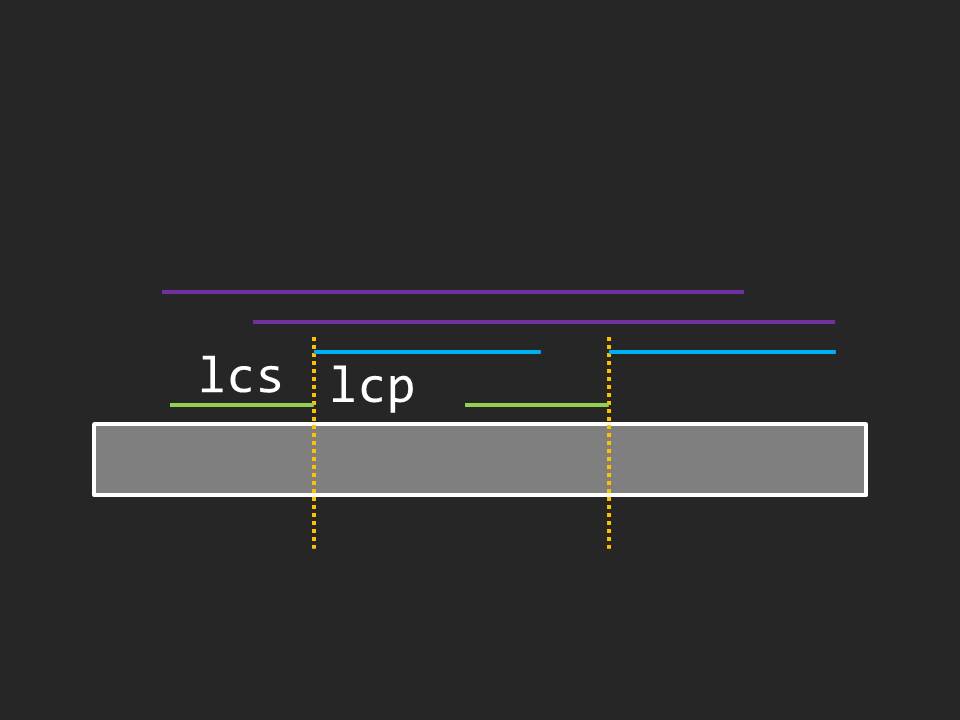
时间复杂度 \(O(n+n/2+n/3+...)\),是个调和级数,所以为 \(O(nlogn)\)
code
[NOI2015]品酒大会
定义两杯酒 p,q 的最大相似值为以 p 开头的后缀和以 q 开头的后缀的 lcp。注意两杯酒如果最大相似值为 r,那么它们的相似值还可以是 [0,r-1]。每杯酒都有一个美味值 \(a_i\),两杯酒调兑之后的美味值为 \(a_i \times a_j\)。
回答选择 \(2\) 杯“\(r\)相似”的酒调兑的数量可以得到的美味度的最大值。
观察到当给相似值单调递减的时候,满足条件的区间个数总是越来越少,而新区间都是两个或多个原区间相连所得,且新区间中不包含在原区间内的部分的 \(hgt\) 值都为减少到的这个值。我们只需要维护一个并查集,每次合并相邻的两个区间,并维护统计信息即可。
code
[AHOI2013]差异
给定一个长度为 \(n\) 的字符串 \(S\),令 \(T_i\) 表示它从第 \(i\) 个字符开始的后缀。求
\[\displaystyle \sum_{1\leqslant i<j\leqslant n}\operatorname{len}(T_i)+\operatorname{len}(T_j)-2\times\operatorname{lcp}(T_i,T_j) \]其中,\(\text{len}(a)\) 表示字符串 \(a\) 的长度,\(\text{lcp}(a,b)\) 表示字符串 \(a\) 和字符串 \(b\) 的最长公共前缀。
被加数的前两项很好处理,为 n(n-1)(n+1)/2(每个后缀都出现了 n-1 次,后缀总长是 n(n+1)/2),关键是最后一项,即后缀的两两 LCP。
我们知道 \(lcp(i,j)=k\) 等价于 \(\min\{height[i+1..j]\}=k\)。所以,可以把 \(lcp(i,j)\) 记作 \(\min\{x|i+1\le x\le j, height[x]=lcp(i,j)\}\) 对答案的贡献。
考虑每个位置对答案的贡献是哪些后缀的 LCP,其实就是从它开始向左若干个连续的 hgt 大于它的后缀中选一个,再从向右若干个连续的 hgt 不小于它的后缀中选一个。这个东西可以用单调栈计算。前面的大于和不小于是为了保证 hgt 权值相等时不会被记重复。
code